ПЕРЕРАБОТКА СЫПУЧИХ МАТЕРИАЛОВ В. МАШИНАХ БАРАБАННОГО ТИПА
ОСЕВОЕ ДВИЖЕНИЕ МАТЕРИАЛА
При использовании гладких вращающихся барабанов или труб, осевое движение зернистого материала определяет производительность дозатора и его точность. Наиболее детальные теоретические и экспериментальные исследования трубчатых дозаторов были проведены в Московском институте химического машиностроения под руководством доцента Ю. А. Репкина. Производительность трубчатого дозатора рассчитывалась по следующей формуле [4, 10]:
(?=Арю</3, (8.28)
где К- коэффициент подачи; р - насыпная плотность сыпучего материала, г/см3; со - угловая скорость вращения трубы, с-1; d - внутренний диаметр трубы, см.
Были получены значения коэффициента подачи для гладких цилиндрических труб и труб, диафрагмированных на выходе. Проведенные экспериментальные исследования показали удовлетворительную сходимость расчетных и экспериментальных данных. Значения коэффициента подачи К могут быть использованы для расчетов основных параметров дозатора. Регулирование производительности осуществляется изменением угла наклона трубы или диаметром диафрагмы. К недостаткам расчетной зависимости (8.28) следует отнести необходимость экспериментального определения значения коэффициента подачи {К) и невозможность прогнозирования точности дозирования.
В работах [26, 27] для описания движения сыпучего материала вдоль оси гладкого вращающегося барабана использован одночастичный подход. Рассмотрены две стадии движения отдельной частицы: подъем частицы вместе с обечайкой барабана; скатывание частицы по внутренней поверхности барабана, во время которого происходит перемещение частицы вдоль оси барабана. Аналитические зависимости, полученные для описания движения отдельной частицы, были затем использованы для описания осевого движения всей массы материала. Основной недостаток данного подхода заключается в том, что он не позволяет описывать движение сыпучего материала в горизонтальном барабане, а тем более в барабане, наклоненном в сторону загрузочного края, что достаточно часто встречается в трубчатых дозаторах. Кроме этого, в расчетные зависимости входит коэффициент, определение численного значения которого требует проведения дополнительных экспериментальных исследований.
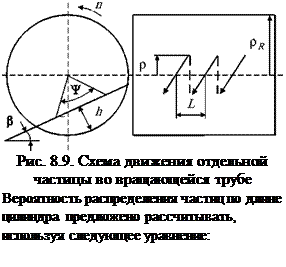
Теоретические и экспериментальные исследования движения сыпучего материала во вращающейся трубе с малым диаметром приводятся в работах [28, 29]. ІТри аналитическом описании осевого движения сыпучего материала авторы данных работ использовали модель, согласно которой осевое перемещение частиц осуществляется за счет их периодического скатывания по открытой поверхности материала, находящегося во вращающемся цилиндре. Схемы движения частиц в поперечном сечении гладкого вращающегося цилиндра и вдоль его оси показаны на рис. 8.9. Путь (А), который проходит частица вдоль оси цилиндра за одно скатывание определяется по формуле:
где р - половина длины хорды открытой поверхности сыпучего материала, для переменного радиуса; а - угол между осью цилиндра и горизонтом (остальные обозначения ясны из рис. 8.9).
Время 0, за которое происходит одно скатывание, определяется по формуле:
9 = -^-, (8.30)
2 кп
где п - угловая скорость вращения цилиндра.
Авторы работ [28, 29] модифицировали понятие о вероятностном характере распределения значения L. С учетом проведенной модификации формула приняла следующий вид:
1=2р(1^Ч1]+р(т,+Т2))’ <fU1)
 |
где уі, Y2 - отклонения отношений S! К от их геометрических значений.
![]()
![]() dP+v? P = D
dP+v? P = D
dt дх “ Эа2
V=±
е
Экспериментальные исследования проводились на трубе с диаметром 7,62 см и длиною 40 см. Угловая скорость вращения изменялась в диапазоне (0,078 - 0,366) от критической. В качестве сыпучего материала использовались частицы с диаметрами: 125,5; 214,5; 387,5 мкм. Исследования проводились при трех коэффициентах заполнения трубы сыпучим материалом: 16,2; 27 и 37,8 %. В работе приводится сравнение расчетных параметров с результатами проведенных экспериментов, а также с опытными данными других исследований. Отмечается удовлетворительная сходимость теории и эксперимента. Работы [28, 29] являются весьма интересными, однако они не могут быть использованы для описания неус - тановившегося режима движения сыпучего материала во вращающемся цилиндре, т. е. когда с течением времени постоянно изменяется степень заполнения цилиндра сыпучим материалом. Применение полученных зависимостей затруднено также нечеткими определениями физико-механических характеристик сыпучего материала, например динамического угла покоя, численное значение которого зависит от угловой скорости вращения цилиндра.
Результаты теоретических и экспериментальных исследований осевого движения сыпучего материала во вращающемся трубчатом дозаторе приводятся в работе [12]. Для определения осевой скорости движения сыпучего материала авторы использовали расчетную схему, представленную на рис. 8.10. Были сделаны следующие допущения:
- коэффициент заполнения трубчатого дозатора материалом в данный момент постоянен по всей длине и равен коэффициенту заполнения в конце процесса;
- загрузка материала в трубе движется без проскальзывания относительно трубы, т. е. коэффициент трения между материалом и трубчатым дозатором равен коэффициенту внутреннего трения материала.
Следует отметить, что второе допущение представляется достаточно обоснованным, а первое не может быть использовано при математическом описании процесса преобразования отдельных порций материала в непрерывный поток. Это объясняется тем, что количество сыпучего материала, находящегося в трубе, периодически изменяется, а следовательно, коэффициент заполнения непостоянен во времени.
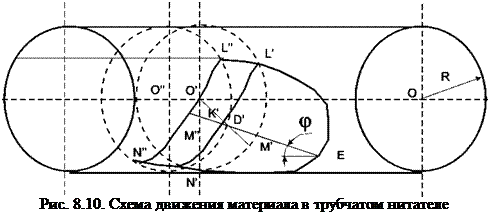 |
Авторы работы [12] приняли следующую схему движения: левее нормального сечения барабана радиусом R, проходящего через центр СГ (см. рис. 8.10), материал совершает циклы подъема частиц с угловой скоростью, равной угловой скорости вращения барабана.
Сегменты подъема ограничены внутренней поверхностью барабана и линиями, лежащими на цилиндрической поверхности раздела, направляющей которой служит линия L'D 'N'. В этой части материал движется по дугам окружности без проскальзывания и вращения частиц относительно друг друга. Возможность скатываться материал получает при входе в область скатывания, лежащую выше поверхности раздела.
|
sin[1] 0(l — |/) 8tgq> cos Є tg 1^,(1+ В)’ |
Правее нормального сечения барабана О' образуется осыпь IC'F'E'N'. При вращении барабана некоторая часть материала из области скатывания переходит на осыпь, скатывается по ней и перемещается вдоль оси трубы. Осевую скорость определяли через количество материала, перешедшее на осыпь, отнесенное к площади Fo поперечного сечения слоя материала при со = 0. Была получена следующая формула для расчета осевой скорости движения:
![]()
![]()
 |
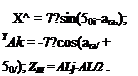 |
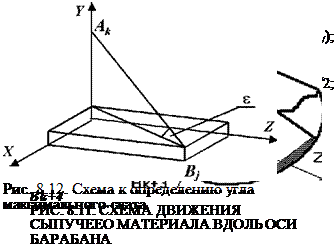
определить координаты точек А* и Bj по формулам, аналогичным (2.15). В системе координат XYZ можно записать:
Из геометрических соотношений значение угла є определяется по следующей формуле:
Изменяя значение j от к + 1 в сторону увеличения, находим значение /П1ах, которому соответствует угол £1Пах максимального ската. При расчете угла максимального ската достаточно легко учитывать угол наклона оси барабана к горизонту ос. В данном случае значения координат ZBj и Z^ необходимо рассчитывать по следующим зависимостям:
Z^ = ^+(7V-l)AZtga; ZBj = ZBj + {N-j)bL.m. (8.37)
Нами были проведены экспериментальные исследования движения сыпучего материала по наклонной изогнутой плоскости. Плоскость с шероховатой поверхностью наклонялась так же, как наклонена открытая поверхность сыпучего материала во вращающейся трубе и условно была разделена на участки от к до j причем участку j соответствовал угол максимального ската. Из точки /Д на плоскость через воронку подавался сыпучий материал (сухой песок). В нижней части плоскости на участках от к до j были установлены ячейки пробоотборника. По количеству материала в ячейке определялось распределение по участкам. Количество участков было от 2 до 4, что соответствовало результатам расчета по формуле (2.28). Результаты эксперимента показали, что при моделировании процесса движения сыпучего материа
ла вдоль оси вращающейся трубы можно сделать допущение о прямой пропорциональности между количеством материала, поступающего на данный участок, и разницей угла ската для данного участка и предыдущего.
Зависимости, полученные в данном разделе, позволяют рассчитывать движение сыпучего материала вдоль оси вращающегося барабана.