Оптоэлектроника

Характеристики непрерывных параметрических генераторов в непрерывном режиме

Вплоть до настоящего характеристики ОРО анализировались в предположении сла­бой эффективности частотного преобразования. Это позволило нам предположить, что пучок накачки остается необедненным и, таким образом, очень удобно упрос­тить теоретические выкладки. В действительности же, как мы теперь увидим, эта аппроксимация очень плохо оправдывается (сообщалось о достижении эффектив­ности преобразования выше 93%!), и сейчас мы попытаемся вывести характеристи­ки ОРО без использования этой аппроксимации.

Для этой цели вспомним уравнения распространения для фаз и амплитуд раз­личных полей (смотрите рис. 12.В.9):

Здесь: ф = ф3~ фх~ ф2 есть относительный нелинейный фазовый сдвиг, а к — нелиней­ный коэффициент связи, определяемый соотношением к = {х{2)/2с)(о)ха)2а)^пхп2п^112. Из соотношения (12.Е.1) можно получить четыре величины, которые постоянны в процессе распространения (при этом три из них являются независимыми):

Эти константы распространения определяются граничными условиями. Более того, закон сохранения энергии может быть легко записан в виде:

Сс^ЬУ + а2и2({у + и^У = 2г°Рс = рс (12.Е. З)

Щ

Здесь: а. = со./со3 — есть квантовые дефекты ОРО, а Рс — полная оптическая мощ­ность, циркулирующая по резонатору.

Резонатор обеспечивает эффект обратной связи применительно к различным рециркулирующим полям, что приводит к следующим стационарным самосогласо­ванным уравнениям для полевых амплитуд Е. между входом при I = 0 и выходом кристалла при г = Ь:

£■ (0)= (I) (12.Е.4)

Здесь: у1Я и 9. есть коэффициент отражения и дефазпровка, вызванная зеркалом, соответственно для сигнальной и холостой волн; Ь' есть длина резонатора за пре­делами кристалла для моды /. С другой стороны, (12.Е.2) и (12.Е. З) гарантирует, что входная и выходная мощности равны и определяются формулой:

= 12°Р^ = и2м = ии + (1 - Л, + (1 - Я2)а2и2и = рои, (12.Е.5) соз

Здесь: и.0 = г/.(0) и и. ь = и.(Ь).

В том случае, когда ОРО работает выше порога в стационарном режиме, часто­ты генерации сигнальной и холостой волн определяются соотношением сохране­ния энергии со1 = а)2 + соу а также уравнением кругового обращения (12.Е.4) для различных полевых амплитуд. В результате этого, характеристики частотной пере­стройки ОРО сильно зависят от величины и резонансной природы различных по­лей в резонаторе, как мы увидим это ниже. Теперь мы исследуем решения этих связанных уравнений соответственно в конфигурациях 81ЮРО и ЭЛОРО.

12.Е.1. ОРО с одиночным резонансном

Таким образом, для конфигурации 8ЯОРО мы предположим, что коэффициент отражения для холостой волны равен нулю, т. е., что г2 = 0. В этом случае самосог­ласованные уравнения записываются в виде:

И,(0)= г{щ(е) (12.Е .6а)

И2 (0) = 0 (12.Е.6 6)

0,(0)—<!>,(/,) =6>, +А:,/, + -^ (12.Е.6<?)

С

При этом мы помним, что полная фаза электрического поля в нелинейном крис­талле составляет ф{(1) + Условие (12.Е.6) означает, что константа движения Г есть Г = 0 в (12.Е.2я) и, таким образом, поскольку их(Ь)и2(Ь)иъ(Ь) Ф 0 выше порога, то СО80(^) = 0. Таким образом, порог достигается, как только фаза ф(£) идентична (л/2) + ртг, где р есть целое число. Знак 8т0 (т. е. четность р) имеет большое значе­ние в (12.Е.1 а—в): он говорит о том, вливается или ли энергия накачки в сигнал или наоборот.

Из (12.Е.1г— е) можно заключить, что три фазы ф.(?) (/ = 1, 2, 3) являются по отдельности постоянными и, в частности, что ф{(Ь) = 0,(0). В этом случае уравне­ние (2.Е.6в) имеет простое следствие:

1с11 + — Ь' + в1 = 2ттг, где т есть целое число (12.Е.7я)

С

Таким образом, мы вновь получаем в нашем общем случае простое и интуитивное условие, что 8 ЛОРО генерирует только тогда, когда сигнальное поле резонансно в резона­торе, что и определяет гребенку возможных сигнальных частот сох или продольных мод подобно тому, как это имеет место в лазере, что дается точным уравнением:

,,гЕЩ

Теперь, используя (12.Е6я) и (12.Е.6б), уравнения сохранения потока (12.Е.2), получаем:

— и2 = /Сд/Ц - и]т, + и22) Это выражение может быть формально проинтегрировано, что дает:
(12.Е.9)
(12.Е.10)
Это последнее выражение представляет собой хорошо известное решение в виде обратных функций Якоби:
(12.E.11)
Представляется не бесполезным напомнить следующее определение обратных функций Якоби:
-і
Sir	(12.E.13)
Уравнение (12.E. 13) является точным и оно дает величину амплитуды сигнала на выходе кристалла в функции входной мощности р. п. Давайте сначала найдем порог генерации SROPO: в этом случае амплитуда сиг­нала u. L -> 0 при ненулевой амплитуде накачки и30 ф 0. Поскольку sn(ix|m) « i sinh(x), когда т -> 0, из (12.Е.13) можно получить величину нормированной пороговой накачки р :
Cosh
(12.Е.14)
KL
Эта есть как раз та величина, которая получается в линейной теории 8ЛОРО(уравнение (12.49); очевидно, что эта теория верна в том случае, когда сиг­нал имеет исчезающе малую амплитуду в кристалле. При введении нормированных переменных X = р. т /р$ и У = и^ /р5 точное уравнение, дающее нормированную мощность сигнала У на выходе кристалла в функции нормированной входной мощ­ности X, принимает вид:
1

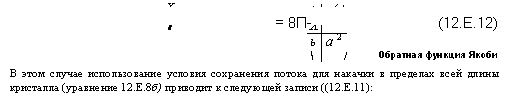Нормированная выходная мощность сигнала ¥' есть произведение У на пропус­кание зеркала, т. е.:

Г=(-Я, У (12.Е.16)

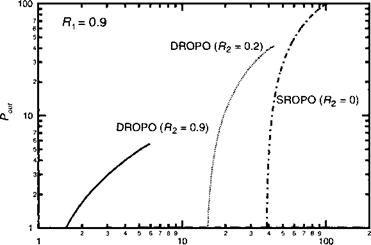
Уравнение (12.Е.15) выполняется для любой величины мощности накачки и его решение зависит от одного единственного параметра: коэффициента отраже­ния для сигнала Яг Оно легко решается с использованием компьютерной програм­мы. В качестве примера на рисунке 12.Е.1 приведены кривые зависимости ¥' от X (т. е. характеристики нормированной величины Роы — Р. п) для коэффициента отра­жения для сигнала Я1 = 90%.

В случае больших значений коэффициента отражения зеркал, т. е., когда

8 = 1 — Ях -» 0, из (12.Е.15) может быть получено ассимптотическое выражение.

С использованием аппроксимации со8Ь_1( 1 /V1 — 8) « ^18 ( 12.Е.15) может быть запи­сано в виде:

-£).,Л (, 2. Е., 7,

Ассимптотическую величину этого последнего выражения достаточно сложно оп­ределить, в случае, когда 8 -» 0. Можно показать, что как только коэффициент отражения превысит 80%, (12.Е.17) станет хорошо аппроксимироваться универсаль­ным соотношением, которое не зависит от коэффициента отражения:

X =—^1= (12.Е.18)

Вш2 л/Г

Вблизи порога (X ~ 1) с использованием разложения в ряд Тейлора это выражение можно записать в следующем виде:

Г = б(УУ-1) (12.Е.19)

Это выражение при выходной мощности на частоте *у,, которая дается выражением Р0ы 1 = 0 "" приводит к соотношению:

= 6А

СОX

(12.Е.20)

Характеристики БЯОРО в непрерывном режиме

Коэффициент пропорциональности 6 в (12.Е.20) является достаточно неожи­данным, но он может быть выведен прямо с учетом того, что сигнальное поле Е{ практически фиксировано в резонаторе и что поля Е3 и Е2 соответственно накачки и холостой волны представляются косинусной и синусной функциями положения в резонаторе.

Внимательный анализ (12.Е.15) показывает, что выходная мощность может быть полностью обедненной (и31 = 0 или, что эквивалентно, X— У') при входной мощ­ности />м1, определяемой соотношением:

( п------ » >

Со.

(12.Е.21)

Это выражение после проведения утомительных операций алгебры эллиптических функций приводит к следующей формуле:

К{т)= |аг/[(1 - г2)(1 - ^2)]'/2

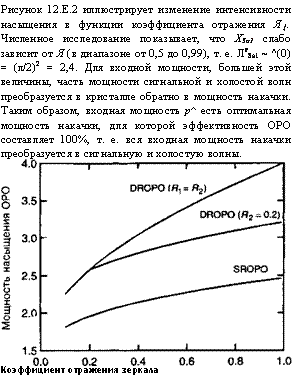Рис. 12.Е.2. Нормированная мощность насыщения ОРО в функции различной величины коэффициента отражения зерка­ла. При этих значениях эффек­тивность ОРО составляет 100%. Одновременно при такой вход­ной мощности происходит пол­ное истощение пучка накачки.