Возмущение вырожденного состояния
Рассмотрим систему, описываемую гамильтонианом #0, обладающую вырожденным состоянием Еп со степенью вырождения gn (т. е. систему с gn независимыми собственными векторами {iffj), / = 1, •••>£„}, образующими подпространство собственных векторов и имеющими одну и ту же собственную энергию Еп). Найдем возмущение, вызываемое в подпространстве собственных векторов, возмущающим полем IV = а(/. Уравнение (1.54) утверждает, что возмущенное состояние всегда принадлежит подпространству собственных векторов, но не дает возможность определить возмущенное состояние |0), поскольку все линейные комбинации собственных векторов \fzj) образуют возможные решения этого уравнения. Таким образом для определения возмущенного состояния |0) необходимо использовать (1.54б). Проецируя (1.546) на векторы iffj), мы находим:
Напомним, что неизвестными являются новое возмущенное состояние |0> и величина возмущения АЕ = аег Уравнение (1.Б.1) есть ничто иное, как уравнение на собственное значение и собственный вектор для оператора возмущения IV в подпространстве собственных векторов {|цгп‘)9 / = 1, ..., gn}. Для большей убедительности на некоторое время обозначим как с. компоненту |0) в базисе у/п‘) (т. е. с. = (у/п‘)) и как у.. элемент матрицы возмущения В этом случае в
Матричной форме уравнение (1.Б.1) запишется в виде:
|
". |
|||
|
• "V • |
С, |
А Е |
С, |
Можем увидеть, что представленное выше секулярное уравнение соответствует диа - гонализации оператора возмущения Ж в подпространстве собственных векторов | у/^).
Для того, чтобы уточнить наши рассуждения обратим наше внимание на пример, иллюстрирующий использование указанного формализма. С этой целью рас-
|
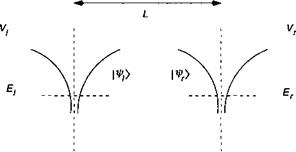
Рис. 1.Б.1. Вырожденная система из двух идентичных атомов, пространственно разнесенных на расстояние Ь. |
Смотрим две идентичные физические системы, далеко расположенные друг от друга (рисунок 1.Б.1).
Система слева центрирована при гп в то время как система справа центрирована при г. Соответствующие гамильтонианы обеих систем имеют вид:
|
Я, |
£ТП
(1.Б. З)
Обе системы обладают подобными гамильтонианами и таким образом имеют идентичные собственные энергии. Например, |/) и |г> обладают одной и той же энергией основного состояния:
|
(1.Б.4) |
![]() Н,1) = Ц1)
Н,1) = Ц1)
|
(1.Б.5) |
![]() Теперь плотно сблизим обе системы таким образом, чтобы каждая из них оказывала возмущающее действие на другую систему. Теперь мы можем представить это влияние в виде гамильтониана возмущения. В этом случае уравнение (1.Б.2) примет вид:
Теперь плотно сблизим обе системы таким образом, чтобы каждая из них оказывала возмущающее действие на другую систему. Теперь мы можем представить это влияние в виде гамильтониана возмущения. В этом случае уравнение (1.Б.2) примет вид:
|
Ч~ |
= А Е |
Ч" |
|
|
_с/_ |
-с/_ |
|
(1.Б.6) |
![]() Без ущерба для общности мы можем предположить, ЧТО Уп = Уи = 0 и что нд являются действительными и равными А. Тогда уравнение (1.Б.5) может быть переписано в виде:
Без ущерба для общности мы можем предположить, ЧТО Уп = Уи = 0 и что нд являются действительными и равными А. Тогда уравнение (1.Б.5) может быть переписано в виде:
|
"0 |
А' |
С„ |
С г |
|
|
Г |
= А Е |
Г |
||
|
А |
0 |
.С!. |
_с/_ |
Из этого следует, что система обладает собственными энергиями и собственными векторами вида:
|
(1.Б.7) |
![]() Е* =Е + А +} = ^(г) + 1))
Е* =Е + А +} = ^(г) + 1))
Е=Е-А -) = ^{г)-1))
|
|
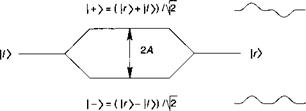
В этом случае основное состояние Е более не является собственной энергией состояний |/> и |г). Можем сказать, что взаимодействие между системами снимает вырождение и что состояния |/) и |г) являются гибридизированными. Схематически этот механизм иллюстрируется рисунком 1.Б.2.
|
Рис. 1.Б.2. Когда два состояния |/> и |г> плотно сближаются, они гибридизируются, снимая вырождение системы. |
Этот механизм образует основу химической связи. Рассмотрим в качестве примера два атома водорода. При большом удалении друг от друга энергия их двух электронов составляет 2Е (где Е представляет энергию основного состояния каждого электрона). По мере сближения сила их взаимодействия IVувеличивается, приводя к снятию вырождения, при этом два электрона на уровне |—) теперь имеют полную энергию 2(Е~ А) (из-за вырождения по спину). Продолжим наше рассмотрение, иллюстрируя его особенно наглядным примером.
Пример: связанные квантовые ямы----------------------------------------------------------------------------------------------------
Прогресс в области синтеза высококачественных кристаллических полупроводниковых гетероструктур обеспечил возможность выращивания квантовых ям, разделенных барьерами толщиной порядка нескольких постоянных решетки (несколько нанометров или несколько больше). Рассмотрим две такие квантовые ямы шириной а, центрированные при +Ь и —Ь соответственно (рисунок 1.Б. З).
|
![]() Примем энергетическую глубину квантовых ям, равной К0. Полный гамильтониан электрона в рассматриваемой системе дается соотношением:
Примем энергетическую глубину квантовых ям, равной К0. Полный гамильтониан электрона в рассматриваемой системе дается соотношением:
|
1 |
||||
|
--------------- 1--------------- 1--------------- Ь |
||||
|
■ ■ ■ *- |
|
-10 0 Положение (нм) |
|
10 |
Рис. 1.Б. З. Снятие вырождения в системе из двух связаннанных квантовых ям за счет электронного туннелирования.
НТ = ^ + У{х-Ь)+У{х + Ь) (1.Б.8)
2т
Где V — ступенчатая функция, равная — К0 в интервале между и —а/2, я/2 и 0 в других областях. Мы уже видели, что можно записать полный гамильтониан в виде суммы невозмущенных гамильтонианов и добавки, связанной с возмущением из-за взаимодействия:
Н = Нг + У(х + Ь)=Н, + У(х-Ь) (1.Б.9)
Каждая яма обладает одной и той же энергией основного состояния £,, определяемой решением уравнения Шредингера. Если глубина квантовых ям К0 достаточна. Волновые функции стационарных состояний в каждой из них приближенно могут быть записаны с использованием (1.44б) в виде:
|
(1.Б.10) |
![]() Ф,(х)« cos к(х + b для -(L/2 + b)<x<-L/2
Ф,(х)« cos к(х + b для -(L/2 + b)<x<-L/2
ФХх)~ л — —e~K(x+L/2 для х > - L /2
Vа ка
|
(1.Б.11) |
![]() Фг0е) ~ JпcosHx - b) для L/2<x<L/2 + a
Фг0е) ~ JпcosHx - b) для L/2<x<L/2 + a
Фг(х)~ ]——e-<x~L/2 для х < L/2 а ка
Ка
Где к и к являются соответственно электронной длиной волны и глубиной проникновения, описываемой (1.33) при L = 2Ь — а. Таким образом, матричные элементы (1.Б.5) легко сосчитать. При этом недиагональные элементы имеют вид:
TOC o "1-5" h z L/2+a а
Wir = ~vo f=------------------------------ f e"'" cos k(u - a/2)du (1.Б.12)
J ка J
L/2 0
что дает после несложных преобразований:
Ж’.e-'i (1.Б.13)
Ка
Аналогичный расчет позволяет определить величину диагональных элементов. Они пропорциональны q~2kL и ими можно пренебречь по сравнению с недиагональными элементами. Связь между двумя квантовыми ямами за счет туннелирования снимает таким образом вырождение системы, приводя к расщеплению величиной 2wlr или:
%е~к1
АЕ ~ —--- Ех (1.Б.14)
Ка
Снятие вырождения системы из двух квантовых ям
Для двух квантовых ям шириной 4 нм с потенциальной глубиной 250 мэВ соотношение (1.43) дает энергию ограничения Е{ величиной 106 мэВ и коэффициент туннельного ослабления 0,502 нм-1. Если две квантовые ямы разделены интервалом в 5 нм амплитуда снятия вырождения составит 34 мэВ. Рисунок иллюстрирует результаты точных расчетов, показывающих, что на самом деле действительная величина расщепления составляет 10 мэВ. Противоречие между двумя величинами происходит из-за того, что аппроксимация бесконечной квадратной ямы недействительна для конечных квадратных ям.