Квантово-размерный эффект Штарка
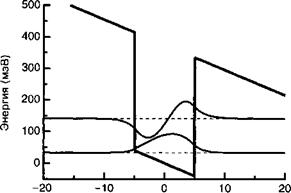
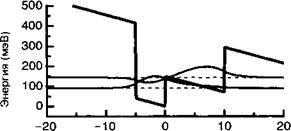
Рассмотрим квантовую яму СаА$/АЮаА$, в которой ось роста задана вдоль направления 01 (смотрите главу 8). Электроны, захваченные зонами проводимости квантовой ямы, описываются делокализованными волновыми функциями |/) и энергией квантования Е. (рис. 1.1). В данном случае нас интересует влияние электрического поля Р, приложенного поперёк структуры, на энергетические уровни в квантовой яме. Используем гамильтониан дипольного возмущения вида:
IV = -$/% (1.В.1)
Если квантовая яма симметрична, то в первом порядке возмущение дает нулевой вклад. В пренебрежении вкладом состояний с высокими энергетическими номерами (/ > 2) соотношение (1.62) дает поправку второго порядка в величину Е. из - за электрического поля:
ДЕ, = Е - Е1 = - ДЕ2 = д*Е* - М-г (1В.2)
Где 1п — элемент матрицы дипольных переходов. Расчет может быть проведен достаточно просто, если используется аппроксимация бесконечной квадратной ямы. Уравнение (1.49) дает выражения для энергетических уровней Ех и Е2, а (1.48) — соответствующие выражения для волновых функций. Интегрирование по ширине ям приводит к выражению для элемента дипольного перехода:
По мере того, как возрастает напряженность электрического поля зазор между энергетическими уровнями увеличивается (смотрите рис. 1.В.1).
Со спектроскопической точки зрения мы можем сказать, что резонансный оптический переход, связывающий эти два уровня, претерпевает голубой сдвиг по энергии на величину:
SHAPE \* MERGEFORMAT ![]()
Или после некоторых упрощении:
|
QFa |
![]()
|
QFa (1.В.5) |
![]() 29
29
АЕ =
3 57Г4
Где Е0 — энергия ограничения из (1.49). Напоминаем, что т* — это эффективная масса электрона, которая в ваАз равна 0,067те. Таким образом, мы видим, что эффект становится более значимым, когда перепад потенциала в квантовой яме qFa становится непренебрежимым по сравнению с энергией квантового ограничения Е0. Теория возмущений явно не срабатывает, когда волновые функции электронов не затухают вне квантовых ям (смотрите рис. 1.В.1). В этом случае электроны в основном состоянии могут туннелировать через треугольный барьер, что приводит к ионизации квантовой ямы электрическим полем.
|
|
|
Положение (нм) Рис. 1.В.1. Квантовая яма, аналогичная представленной на рис. 1.1, в условиях статического электрического поля. Энергетический зазор между двумя энергетическими уровнями возрастает в результате действия приложенного электрического поля. Это приводит к голубому сдвигу из-за эффекта Штарка. |
Пример---------------------------------------------------------------------------------------------------------------------------------------------------
В квантовой яме GaAs толщиной 12 нм и эффективной массой электронов т' = 0,067 те штарковский сдвиг АЕ = 29/(3 х жА) х (105 х В/см х 106 см)2/0,115 эВ или 2 мэВ ожидается для напряженности электрического поля 10 В мкм-1. Этот сдвиг огромен в сравнении с тем, что может быть индуцировано в атомах. Это же является прямым следствием малой эффективной массы электронов в GaAs, а также значительно больших напряженностей электрических полей, которые могут быть индуцированы в структурах на основе конденсированных сред, сформированных с использованием традиционных методов изготовления микроструктур (A. Harwit and J. J. Harris, Appl. Phys. LeU. 50,685(1987)).
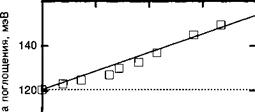
Отмеченный сдвиг имеет важное значение, так как его величина может превышать ширину линии для перехода Е{ -> Е2 (с типичной величиной 5 мэВ) и он впервые наблюдался Харвисом и Томсоном (1987). Рисунок 1.В.2 иллюстрирует сравнение их экспериментальных результатов с теоретическими данными.
|
|||||
|
|||||
|
|||||
|
|||||
|
|
|
|||
|
|||||
|
80 |
![]() 20 40 60
20 40 60
Напряженность поля, кВ/см
Рис. 1.В.2. Наведенный эффект Штарка в оптических переходах симметричных и асимметричных квантовых ям. Различный характер процессов в этих квантовых ямах обсуждается в двух примерах, рассмотренных ранее.
Как видно, полученные экспериментальные результаты для симметричной квантовой ямы согласуются с параболической зависимостью штарковского сдвига от напряженности электрического поля.
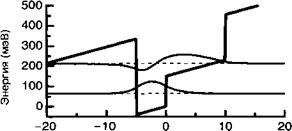
Если квантовая яма асимметрична (смотрите рис. 1.В. З), то возмущение первого порядка не равно нулю и составляет:
A E = qFSn (1.В.6)
Где 6п = (1Й1) — (2|z|2) и представляет собой смещение среднего положения электрона из состояния |1) в состояние |2).
Пример-----------------------------------------------------------------------------------------------------------------------------------------------------
Для квантовой ямы, представленной на рис. 1.В.2, решение уравнения Шредингера дает дипольное смещение амплитудой 4,2 нм. При этом штарковское смещение для перехода Е{ -> Е2 составляет 42 мэВ при напряженности поля 10 В/мкм. Таким образом этот эффект в первом порядке играет существенно более важную роль, чем в предыдущем примере для симметричной квантовой ямы (Е. Martinet, F. Luc, Е. Rosen - cher, P. Bois, E. Costard, S. Delaitre and Bockenhoff, in Intersuddand Transitions in Quantum Wells, edited by E. Rosencher, B. Vinter, and B. Levine, Plenum, London (1992) p.299).
Этот эксперимент был осуществлен с использованием асимметричных структур ваАБ /ваЛЬА*. На рис. 1.В. З представлены экспериментальные результаты для величины штарковского сдвига в функции напряженности приложенного электрического поля. В представленных данных четко прослеживается линейная зависимость сдвига резонансного перехода от напряженности электрического поля, кото-
|
Положение (нм) |
|
Положение (нм) Рис. 1.В. З. Асимметричная квантовая яма в условиях воздействия электрического поля. |
|
|
Рая согласуется с предсказаниями (1.В.6) для параметров, использованных в приведенном выше примере. Указанный пример был использован в новом поколении инфракрасных детекторов и будет более углубленно рассмотрен в главе 11.