Трехмерные экситоны
Попытаемся описать состояние электронно-дырочной пары с учетом взаимодействия их противоположных зарядов. Очевидно, что нам необходимо двухчастичное состояние, т. е. являющееся результатом тензорного произведения (смотрите уравнение (2.48)) электронного и дырочного состояний. Двухчастичная волновая функция может быть представлена в виде ряда по блоховским функциям для электронов и дырок:
(Кг1> Г,) = 77т Y, C(kl’ k2)eik|' (г, )е (г2)= ХС(к'’Мк,>кг) (8 БЛ)
В этом случае состояние двух частиц дается решением двухчастичного уравнения Шредингера:
_ 2
|
(8.Б.2) |
![]()
|
^(r„r2)= Ј^(r,,r2) |
![]() -Р-*Р - + УЛ^) + УЛь)—г-т------------- I
-Р-*Р - + УЛ^) + УЛь)—г-т------------- I
2me 2mh 4яе|г, - r2|
Давайте подставим в это последнее уравнение (8.Б.1) и спроецируем результат на |к',к2), что дает:
Ее + + -^Г|С(к„ к2) + У С(к[, к'2)(к„ к2 |К(г, - г2)|к;, к'2) = £С(к„ к2) (8.Б. З)
АГПе ^ £^4
Используя тот факт, что потенциал взаимодействия медленно изменяется по отношению к размерам элементарной ячейки, используем тот же ход рассуждений, что и ранее и (смело!) введем огибающую функцию с тем, чтобы упростить матричный элемент:
/ I I. 1 Г i(k'-k,) (г,-г2)
(к„ к, |К(г, - г,) к;, к;) = - V dr, dr, e V(г, - Г,)е
Q, J
1 Г ~ i(k',-k2-k; + k.)r, 1 ~ 1 ~
= ^-Jdr2K(k1 - к2)е = ±Aw k K+k V(ki _ к'2) = _k qK(q)
|
(8.Б.4) |
![]() I(k'-k2-k; + k,) г,
I(k'-k2-k; + k,) г,
Здесь:
Это выражение представляет собой Фурье-образ кулоновского взаимодействия. Для получения (8. Б.4) мы предположили, что периодические части блоховских функций не зависят от к.
В этом случае мы можем записать уравнение Шредингера (З. Б.З) в виде:
|
Е + |
![]() + ^(к к } + у К(ч)С(к _ ч к2 + „) = ЕС{к„ к2) (8.Б.6)
+ ^(к к } + у К(ч)С(к _ ч к2 + „) = ЕС{к„ к2) (8.Б.6)
2т, 2тъ ]
Поскольку к1 + к2 сохраняется в члене взаимодействия, представляется целесообразным провести замену переменных к, и Ц на новые переменные Кик, где:
К _ к, к2
К = + (,Б.„
Здесь М = те + тк есть полная масса, а /тг = (1 /те) + (1 /тк) определяет приведен
Ную массу тг. С этими новыми переменными мы имеем:
С(к„ к2) = С (К, к) (8 Б 8)
С(к, - ч, к2 +4) = С(К, к + ч)
При этом уравнение Шредингера приобретает вид:
Е’* + ~Ш~ + ^<К’ к) + X ^Ч)С(К, к + ч) = ЕС (К, к) (8.Б.9)
Г ) Ч
Сумма по ц обусловлена взаимодействием между электроном и дыркой и касается только второго члена аргумента для С. Это означает, что ЦК, к) допускает разделение переменных и может быть записано в виде С(К, к) =ДК)#(к), где #(к) должно подчиняться соотношению:
Е*+ ~Ш'+^Г^(к) + X '7(ч)^(к + ч) = ^(к) (8Б10)
Г ) я
Теперь мы можем ввести огибающую функцию для относительного движения:
*(г) = 2>(к)е - (8.Б.11)
К
В этом выражении мы узнаем определение, эквивалентное (8.12). Используем ту же процедуру, что и при получении из (8.14) уравнения (8.17), что дает уравнение Шредингера (8.10) в реальном пространстве:
ЙЧ2 , , „ ПгКг
|
—£(г) + К(г)#(г) = |
![]()
|
2т, |
![]() Е~Ч*г~Е* ^(г) (8Б12)
Е~Ч*г~Е* ^(г) (8Б12)
В этом выражении мы узнаем уравнение Шредингера для атома водорода (или лучше сказать, для позитроний.). В этом случае допустимые величины энергии составляют:
|
=£,+-^77---------- п = 1,2,... |
![]() П2К2 Яу*
П2К2 Яу*
2М " (8.Б.13)
Яу* = - Ц-Ку £-
Здесь: Яу есть энергия ионизации 5-состояния атома водорода. Эта величина известна как Ридберг и она равна 13,6 эВ. Как мы это могли и ожидать, взаимодействие между электроном и дыркой создает дискретные состояния в запрещенной зоне, через которые электрон и дырка связываются друг с другом (с точки зрения их относительного движения), сохраняя при этом свободу перемещаться по кристаллу как пара. Член Н 2К2/2М соответствует кинетической энергии, связанной со свободным движением центра масс двух частиц. При энергии, большей Е + Н 2К2/2М, мы имеем континуум разрешенных энергетических со
стояний. Этот континуум соответствует возбуждению системы, которое приводит к эффективному освобождению электрона и дырки от их взаимной связи. Рисунок 8.Б.1 иллюстрирует спектр возбуждения полупроводника.
Взаимодействие системы с электромагнитной волной сохраняет полную энергию и импульс. Это означает, что К = ч * 0, где ц есть волновой вектор фотона. Таким образом спектр поглощения содержит ряд дискретных линий в запрещенной зоне, а также область континуума при Ь со >
Помимо проявления дискретных линий в спектрах поглощения электроннодырочная корреляция в полупроводниках имеет и другие следствия. Поглощение континуума также увеличивается вблизи края запрещенной зоны. В результате этого поглощение в функции энергии фотона проявляет разрыв вместо более мягкой зависимости вида (Нсо~ Е)1/2, рассчитанной в Главе 7. Этот эффект, описываемый коэффициентом Зоммерс$ельда, обусловлен пространственным перекрытием волновых функций электрона и дырки вследствие взаимодействия, которое стремится приблизить обе частицы друг к другу. На рис. 8.Б.2 приведено сравнение усиленного поглощения вследствие экситонных состояний с поглощением в рамках одноэлектронной модели.
Пример----------------------------------------------------------------------------------------------------------------------------------------------------
1. Экситоны в ваАБ.
В случае СаАБ мы имеем те = 0,067аи0, тнн = 0,51 т0 и е— 2е0. Энергия связи экситона для п = 1 составляет:
|
|
Мы видим, что величина Ев мала по сравнению с квТ при комнатной температуре. В результате этого связанным экситон может оставаться только при очень низких температурах. Среднее расстояние между электроном и дыркой в экситон - ном состоянии с п = 1 составляет (по аналогии с боровским радиусом в атоме водорода):
|
* тп ав ~ |
![]()
![]() ^ 0,052 нм = 10,6 нм 0,059
^ 0,052 нм = 10,6 нм 0,059
Е
|
|
|
|
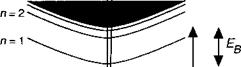
Рис. 8.Б.1. Спектр возбуждения полупровод-
Ника отражает присутствие связанных экситонных состояний в запрещенной зоне. Связь с фотоном, имеющим волновой вектор ч, обеспечивает сохранение полной энергии и импульса. Таким образом, спектр поглощения состоит из набора дискретных линий, за которыми следует континуум.
|
|
|
Поглощение
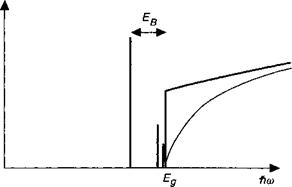
Рис. 8.Б.2. Экситонная корреляция между электроном и дыркой модифицирует спектр поглощения. По сравнению с «некоррелированным» спектром (тонкая линия) в энергетической зависимости поглощения проявляются резкие экси - тонные резонансы в области ниже края запрещенной зоны, а также резкое возрастание поглощения в области слегка выше края поглощения. |
Это согласуется с предположением о медленно меняющейся огибающей функции по сравнению с размерами элементарной ячейки.
2. Экситоны в Са1Ы
Для широкозонного полупроводника, каким является Са1Ы, £ = 3 4 эВ, те = 0,22т0, тш ~ т0 и е = 9,8б*0, при этом приведенная масса составляет 0,18 т0, Ев —26 мэВ и а*в= 2,8 нм. В результате этого экситонные эффекты намного более важны в широкозонных полупроводниках. При комнатной температуре доля 1 — ехр(—26/25,9) или 64% генерированных экситонов останется в связанном состоянии.