Оптоэлектроника

Суммарная частота, разностная частота и параметрическое усиление

В начале раздела 12.2 мы видели, что взаимодействие между тремя волнами с час­тотами (ov (о2 и а)3 в кристалле, обладающем нелинейной восприимчивостью второ­го порядка, приведет к генерации суммарной и разностной частот. К тому же мы только что видели, что в этом случае могут возникнуть параметрические колеба­
ния. Сейчас пора провести различие между этими различными режимами. В связи с этим мы рассмотрим две волны с круговыми частотами со2 (накачка) и (ох (сигнал), падающие на нелинейный кристалл. Предположим о)2 > cov Уравнение (12.38) ука­зывает на три процесса, которые мы можем ожидать:

Генерация разностной частоты (DFG) со — а)2 — оох

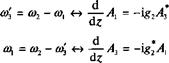Предположим, что ориентация кристалла была выбрана таким образом, чтобы удов­летворить условию фазового согласования DFG, а именно Дк = Ц — kt — к'3 = 0. После небольших изменений в обозначениях два соответствующие уравнения (12.38) могут быть записаны в виде:

(12.64)

Здесь: g2 = кА2 и эту величину можно считать действительной. Эта система может быть тривиально решена с тем, чтобы получить эффективность преобразования, соответствующую отношению преобразованной мощности Р3(Ь) к мощности пада­ющего сигнала Р{(0):

(12.65)

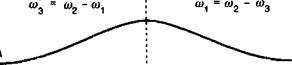
Энергия передается от сигнальной волны сох волне с разностной частотой о'3 и волне накачки о>2. В терминах числа фотонов (смотрите главу 2) это может быть записано как |п{9 п2, п) -> п{ — 1, п2 + 1, п'3 -1). В конце пути Ь = л/2#2 процесс передачи энергии меняет свое направление и фотоны волн с частотами со и (о2 рекомбинируют, усиливая сигнальные фотоны с частотой сор что может быть запи­сано как |п{, п2, п) -> |пх + 1, «2 — 1, «з — 1) (смотрите рис. 12.9). Как следствие этого, в параметрических взаимодействиях могут проявляться процессы «расщеп­ления» фотонов и рекомбинации. В дополнении 12.Е мы увидим, что превалирую­щий механизм зависит от относительной фазы каждой волны по отношению к другим волнам.

Заметим, что даже при максимальной эффективности преобразования (т. е. при ^ = л/2) эффективность преобразования не может превысить единицу:

(12.66)

Это последнее выражение напоминает нам о том факте, что параметрическое пре­образование фотона с энергией Н сох в фотон с меньшей энергией Ь со' не может происходить с эффективностью, большей Ь,(о1%(ох. При малой величине эффек­тивности по сравнению с единицей (12.65) может быть записано в более простом виде, если мы заметим, что:

(12.67)

С использованием (12.44) для выражения g2 в функции электрического поля Е2 и

(12.32) Для выражения Е2 в функции мощности на единицу поверхности Р2 это дает:

РЛР

/»(0) 2п, п2п.

Эффективность преобразования для оптических частот

Таким образом, мы приходим к выражению, аналогичному уравнению (12.33), полученному в контексте генерации второй гармоники.

Генерация суммарной частоты (вРв) а)3 = о)2 + сох

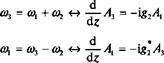Сейчас мы вновь предположим, что ориентация кристалла была выбрана таким образом, чтобы удовлетворить условию согласования фаз в процессе БРв, а именно: Дк = Ц, + Ц — 1ц= 0. В этом случае два соответствующие уравнения (12.38) принимают вид:

(12.69)

Как и ранее, эта система уравнений может быть тривиально решена. При этом полученный результат будет носить характер, идентичный приведенному ранее в

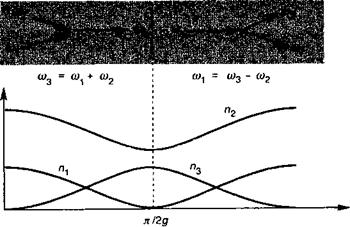
(12.65) . Однако, на этот раз энергия переносится от сигнальной волны и волны накачки к волне с суммарной частотой сог На языке числа фотонов это записыва­ется в виде |п19 п2, п3) -> пх — 1, п2 — 1, «з + 1). В конце пути Ь = п/2g2 процесс переноса энергии меняет свое направление и фотоны волны суммарной частоты со3 «фрагментируются» в фотоны с частотой со2 и сох Этот процесс может быть записан в виде |пх, п2, п3) -> |п1 + 1, п2 + 1, «з - 1) (смотрите рис. 12.10).

Уравнение (12.69) очень похоже на (12.64) при обсуждении процесса генерации разностной частоты. Таким образом, выражение (12.68) имеет тот же вид и для процесса генерации суммарной частоты. В дополнение к этому в рассматриваемом случае максимальная эффективность определяется выражением:

(12.70)

Таким образом, эта эффективность может превышать единицу. В этом факте нет ничего необычного, т. к. увеличение мощности пучка из-за преобразования фотонов с энергией Ьсох в фотоны с меньшей энергией Ьсоъ происходит за счет фотонов пучка накачки.

Таким образом, какой из двух процессов (генерации суммарной или разно­стной частоты) будет иметь место, определяется тем, какое из двух условий согла­сования фаз (соответственно к3 = Ц + Ц или к' = к'2 — к^ реализуется.

Параметрическая генерация

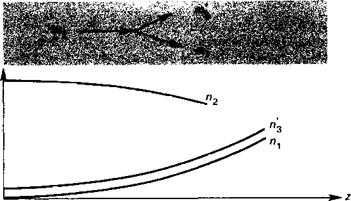
Этот случай отличается от двух, рассмотренных выше. При параметрической гене­рации фотоны пучка накачки с энергией Нсо2 спонтанно «расщепляются» в пары фотонов с меньшей энергией Ьох и Нсо'’ (смотрите рис. 12.11). Под словом «спон­танно» в данном случае подразумевается то, что рождение фотонов с энергиями происходит без какого-либо воздействия извне.

По аналогии с (4.28а, б) из раздела 4.6 по лазерной генерации, а также с учетом уравнений Мэнли—Роу, мы могли бы сделать заключение, что выходная мощность параметрического генератора дается выражением:

НЕПРАВИЛЬНО!

Здесь Р2 1ЬгезЬо1(1 определяется условиями генерации (12.50) или (12.62). Это уравне­ние является следствием ложной интуиции и хотя используется многими авторами, оно никогда не подтверждается экспериментально, т. е. оно действенно лишь в

Очень ограниченном диапазоне. В действительности ситуация намного более слож­ная, и она обсуждается в дополнении 12.Е (смотрите уравнения 12.Е.20) и (12.Е. ЗЗ).

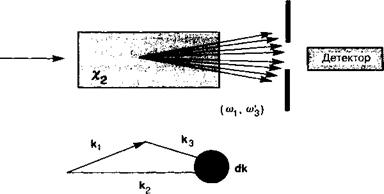
Спонтанное рождение фотонов с энергией Нсох и й со'3, которые необходимы для «затравки» ОРО-генерации, связано с параметрической флуоресценцией. Это физи­ческое явление не может быть описано в рамках классического подхода, разрабо­танного выше (это подобно тупику, к которому мы в свое время пришли при об­суждении лазерной генерации, что продиктовало необходимость введения в нашу модель спонтанной эмиссии — смотрите главу 4). Рисунок 12.12 иллюстрирует ус­ловия, при которых может наблюдаться рассматриваемый эффект. Поток накачки с фотонами, имеющими энергию Нсо2 и волновым вектором к2, падает на нелиней­ный кристалл. На одной оси с падающим пучком мы поместили детектор, чувстви­тельный только к фотонам с энергией Ьсох и й со. Диаграмма направленности экс­периментальной системы такова, что могут детектироваться лишь фотоны, возни­кающие в нелинейном кристалле и обладающие волновым вектором к2 в пределах (1к (смотрите рис. 12.12).

В процессе параметрического взаимодействия может быть спонтанно создан ансамбль фотонных пар (Ьсох, Ьсо3) с Нсох + Ьа)3= Нсо2. Поскольку в этом процессе преобразования частоты должен сохраняться импульс, детектироваться будут лишь пары фотонов с полным импульсом к1 + к' и в пределах входной апертуры прием­ника излучения. Именно эта параметрическая флуоресценция ответственна за за­пуск параметрической генерации.