Спонтанная эмиссия в полупроводниковых лазерах
При предыдущем рассмотрении мы пренебрегали влиянием спонтанной эмиссии на характеристики полупроводниковых лазеров. В связи с тем, что полупроводники обеспечивают большое усиление, имеет место и значительное усиление спонтанной эмиссии (что называется А8Е или усиленной спонтанной эмиссией). В свою очередь, оказывается, что А8Е играет фундаментальную роль в определении основных характеристик лазерных диодов. В связи с этим настоящий раздел посвящен исследованию влияния этого эффекта на функционирование лазерного диода.
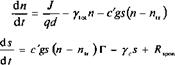 Система уравнений (13.69) описывает связь между концентрацией носителей п и плотностью фотонов 5 в резонаторе. Как мы отмечали в разделе 4.А, для учета спонтанной эмиссии, нам необходимо только добавить член (независимый от числа фотонов 5) для дополнительной скорости /?зроп генерации фотонов. В этом случае уравнение (13.69) принимает вид:
Система уравнений (13.69) описывает связь между концентрацией носителей п и плотностью фотонов 5 в резонаторе. Как мы отмечали в разделе 4.А, для учета спонтанной эмиссии, нам необходимо только добавить член (независимый от числа фотонов 5) для дополнительной скорости /?зроп генерации фотонов. В этом случае уравнение (13.69) принимает вид:
(13.Д.1)
Скорость излучательной рекомбинации была рассчитана в главе 7 и дается уравнением (7.61): /?5роп = у п. Здесь ^роп есть скорость спонтанной эмиссии, определяемая узроп = Вр, где р (= п, если мы по-прежнему считаем, что излучатель - ная рекомбинация имеет место в нелегированной области) есть концентрация дырок, а В — коэффициент бимолекулярной рекомбинации. Тем не менее, мы должны учесть, что не все фотоны, излученные в активной области переходят в волноводные моды (смотрите рис. 13.Д.1). Только доля /? спонтанно излученных фотонов (называемых коэффициентом спонтанной эмиссии) переходит в волновод и усиливается. Расчет для получения этого коэффициента (3 достаточно сложен и не является достаточно надежным. В связи с этим, общепринятая практика заключается в том, чтобы рассматривать у3 в качестве подбираемого параметра (т. е. определяемого согласованием кривых), при этом его величина лежит в диапазоне между 10~4 и 10~5 для реберных волноводных лазеров.
Волноводный слой
Активный слой
У
Волноводный слой
Рис. 13.Д.1. Только ЛИШЬ часть /? излученных структурой фотонов переходит в волноводную моду и испытывает усиление.
В стационарном состоянии выражение (13.Д.1) определяет концентрации электронов и фотонов:
|
7 si |
![]() D
D
Spon____________ _ Р__________
Tc'g(n-nu) Yc
Ус ~ 1 CW -К) Ус -Гс'«(и-и, г)
J (13. Д.2)
---- = У,О," + c'g(/J - и„)5
Qd
Первое их этих двух уравнений является особенно полезным и оно отражает тот факт, что лазерные колебания возникают из спонтанной эмиссии, как только усиление превысит резонаторные потери. В этом случае пороговая концентрация «threshold дается выражением:
|
= п, г + |
![]()
|
Г c'g |
![]() (13.Д-3)
(13.Д-3)
Второе уравнение в (13.Д.2) может быть выражено более кратко за счет введения безразмерных переменных:
|
(13.Д.4) |
![]() Х = —; у = и а - A2thrgs-|10ld = 1 + —— "tr К К TcgA2tr
Х = —; у = и а - A2thrgs-|10ld = 1 + —— "tr К К TcgA2tr
Здесь /1г= цс1ушпх — плотность тока прозрачности. Таким образом, мы устанавливаем четкую связь между концентрацией носителей и током накачки, которая может быть записана в компактном виде:
Р х(х -1)
|
(13.Д.5) |
![]() У = х + ^Л—-
У = х + ^Л—-
Г а - х
Здесь г] — квантовая эффективность, определяемая как г) = У5роп/У^ = ^оУ^роп* Для того, чтобы найти зависимость 5(У) плотности фотонов от тока накачки, нам необходимо только решить это уравнение и подставить его в первое уравнение (13.Д.2), что дает:
S = nitp(a -1)2*»
(13.Д.6)
Ус ос-х
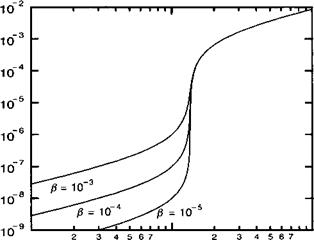
Уравнения (13.Д.5) и (13.Д.6) являются двумя параметрическими уравнениями по х, которые позволят нам рассчитать характеристики 5(У). Если /3 = 0, то мы вновь получаем характеристику лазерного диода, подробно описанную в главе 13, в соответствии с которой концентрация носителей п увеличивалась пропорционально электрическому току / = ду1о1с! п в области ниже порога и резко фиксировалась на уровне п = пи в области выше порога. Если /3 ф 0, то зависимость носит более плавный характер, описываемый рисунком 13.Д.2.
|
0.1 1 10 |
J/Ju
Рис. 13.Д.2. Изменение плотности фотонов S (нормированной к пороговой концентрации носителей пи) в функции плотности тока накачки (нормированной к плотности тока прозрачности /tr) для различных значений коэффициента спонтанной эмиссии Д Другие используемые параметры приведены в примере, который приводится ниже.
Пример---------------------------------------------------------------------------------------------------------------
Кривые на рис. 13.Д.2 были рассчитаны в предположении квантовой эффективности т/ = 0,5, резонаторного времени жизни г = 2 пс, времени жизни спонтанной эмиссии rspon = 2 не, коэффициента ограничения Г = 0,5, концентрации носителей в режиме прозрачности Пи =1,25 х 1018 см-3 и динамического усиления G =2,5 х 10-16 см2 или А= 1,352. Программа MATHEMATICA, приводимая ниже, может быть использована для получения лазерных характеристик ниже порога.
Beta=.;gamma =0>5;tauc=1/2(2.10,'-12);taus=1/(2.10''-9); eta=0.5;g=2.5 10~-16;ntr =1.25 10" 18;nop=3.3; c’=3.10Vnop;
Alpha =1+tauc/(gamma)*c’*g*ntr);
R=taus/tauc;
Betap=(alpha —1 )*R;
Eq1 =yp = = alpha*zp/(zp+betap)+beta/betap*zp*
(alpha*zp/(zp+betap)-1 ) sol=Last[Solve[eq1 ,zp)]; t=zp/.sol;
Needs[ “Graphics’Graphica”’]
Beta =10" 1-4;
Plotl = LogPlot[t,{yp,.01,2}] beta =10~-3; plot2=LogPlot[yp,.01,2] beta=10~-5;
Plot 3=LogPlot[t,{yp,.01,2]
Show[plot1 ,plot2,plot3]
Рисунок 13.Д.2 может быть интерпретирован следующим образом: ниже порога фотоны спонтанно переходят в волноводную моду резонатора (в этом режиме лазерный диод ведет себя как СИД). Выше порога плотность фотонов существенно возрастает (как это описывалось ранее в дополнении 4.А). Более того, как видно из рисунка 13.Д.2 пороговый эффект становится все более мягким по мере того, как коэффициент Р стремится к 1.
Эта картина была еще более уточнена Yamamoto с сотрудниками. Этот автор отметил, что само по себе динамическое усиление g дается g = PS/rspon, где S есть площадь поверхности образца. При подстановке этого выражения в (13.Д.5) и (13.Д6) ему удалось показать, что по мере того, как /3 стремится к 1, лазерный порог стремится к нулю. Из этого наблюдения возникала концепция лазера с нулевым порогом, в котором все спонтанно излученные фотоны дают вклад в лазерную эмиссию в режиме усиления.
Представляется интересным использовать настоящую модель для описания многомодового характера полупроводниковых лазеров вблизи порога. Для этого предположим, что в резонаторе одновременно существует т мод. Эти моды характеризуются межмодовым частотным интервалом Avcav = cf/2L. Таким образом, каждая из т мод описывается уравнением типа (13.Д.1) с учетом дополнительной возможности, что параметры g и р изменяются в соответствии с модовым коэффициентом преломления:
|
(13.Д.7) |
![]()
|
Dsw d t |
![]() Dn J v1 / /
Dn J v1 / /
= C'Smsm(n - Or - YcK + PmySpoi
Лазерные уравнения для однородного усиления
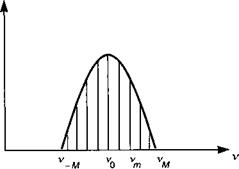
Отметим, что в этих уравнениях все моды характеризуются одной и той же инверсией заселенности п, которая, по определению, означает, что лазерная среда предполагается однородной. Предположим, что кривая усиления имеет вид лорен - циана, смотрите рис. 13.Д. З:
|
|
8 о |
|
8 о |
|
G = |
|
I + [(к - »'о )/ Д У Р |
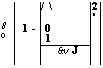 |
|
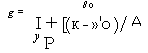 |
|
|
|
Очевидно, как это следует из глав 7 и 13, полупроводниковые усиливающие среды по своей природе обладают более сложными кривыми усиления. Таким образом, эта формула предлагает лишь аппроксимацию более точной ситуации (в то же время она достаточно хорошо согласуется с экспериментом). При записи пол - Усиление
|
Рис. 13.Д. Э. Аппроксимация параболической огибающей кривой усиления для полупроводникового лазера. Число усиленных мод составляет 2М + 1. |
|
_______ 1 - (т / М У_________ (а - 1)- (х - і)[і - (т/ М )2] |
|
Т-М |
|
2 а - х є = ■ |
|
(13.Д.116) |
|
Х -1 |
|
Эти уравнения следует интерпретировать с использованием абсолютных значений комплексных величин, если є2 < 0. Аналогичным образом, плотность фотонов Бт для моды т получается в соответствии со стационарной величиной второго уравнения (13.Д.7), т. е.: |
|
1 Х -1 |
|
Т ~М |
|
1 + |
|
А - х |
|
(13.Д.13) |
|
7с а ~ х Здесь для упрощения рассмотрения мы предположили, что коэффициент спонтанной эмиссии /3 не зависит от моды. Такой подход позволяет сделать ряд заключений. Начнем с того, что хотя мы предположили, что система однородно уширена, мы замечаем (смотрите рис. 13.Д.4), что в резонаторе может существовать несколько лазерных мод. Излучение этих мод вводится в действие спонтанной эмиссией (что описывается Д заметим, что, если Р = 0, то 5т = 0). Более того, по мере того, как ток накачки становится большим (у —> °°), нормированная концентрация носителей х стремится к а и становится фиксированной. В то время, как плотность фотонов 50 в центральной моде стремится к бесконечности, плотность фотонов в моде т насыщается в соответствии с соотношением: |
|
— (і + Є 2)агсІап Є |
|
У = х + 2р - рх |
|
+1 ! |
|
1-й2 |
|
У = X + Р~Х |
|
-йи |
|
Г г, [а- / х-)-]+и2 Это уравнение может быть точно решено, что дает: |
|
|||||
|
|||||
|
|||||
|
|||||
|
|||||
|
|||||
|
|||||
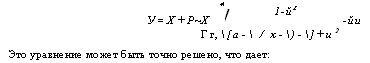 |
|||||
|
|||||
|
|||||
|
|||||
|
|||||
 |
|||||
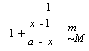 |
|||||
|
|||||
|
|||||
 |
|
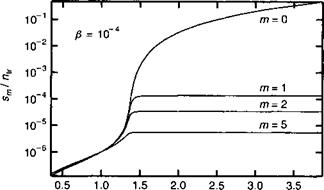
J/Jtr Рис. 13.Д.4. Изменение плотности фотонов sm моды т (нормированной к концентрации носителей в режиме прозрачности ntr) в функции плотности тока накачки J (нормированной к плотности тока прозрачности Jtr) для коэффициента спонтанной эмиссии /? = 10~4. Другие используемые параметры приведены в следующем ниже примере. |
Таким образом, интенсивность поперечных мод спадает до нуля по сравнению с интенсивностью центральной моды. Такой характер зависимости воспроизводится экспериментально и приводится на рис. 13.Д.5.
Пример---------------------------------------------------------------------------------------------------------------
Как развитие предыдущего примера программа MATHEMATICA, приведенная ниже, может быть использована для расчета характеристик многомодового лазера в функции тока накачки вблизи порога.
М=10; beta=1CT-3; x=alpha-u; z=betap*(alpha/u-1); eps=Sqrt[u/ (alpha-1 - u)];
Y=Abs[x+2*beta*((1+eps~2)/eps*ArcTan[1/eps]-1)];
M=1;
Z1=z*1/(1+((x-1)/(alpha-x)*(m/M)''2)); tableyl =Table[{y, z1}, {u, 1СГ-6,1СГ-4,10^-6}]; tabley2=Table[{y, z1}, {u, 1СГ-4,1СГ-2,10Л-4}]; taabley3=Table[{y, z1}, {u, 1СГ-2,1., 1СГ-2} ]; tablep=Join[tableyp1,tableyp2,tableyp3]; p2=LogListPlot[tablepy]