Соотношения Мэнли—Роу
Анализ (12.27) выявляет недостаток эстетической симметрии между представленными уравнениями (присутствие различных (о. и п. в каждом уравнении). Для того, чтобы сделать эти уравнения симметричными, Мэнли и Роу предложили ввести следующие величины:
А, = - Ее, (12.35)
со,.
Эти модифицированные амплитуды интересно использовать по той причине, что они непосредственно связаны с потоком фотонов Фг / с энергией Н со.. В действительности, мощность излучения дается выражением:
|
|
Так, что:
|
|
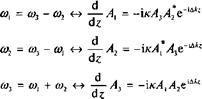При этом в этих выражениях не появляются ни о)р ни п.. Подставляя вновь введенные амплитуды в уравнения преобразования (12.27), мы получаем более симметричную систему:
(12.38)
Нелинейные уравнения связи между потоками фотонов
Здесь: к — коэффициент нелинейной связи:
(12.39)
Уравнение (12.39) будет особенно эффективным, если мы можем предположить, что материал не обладает дисперсией (т. е., что &к = 0). Как мы увидим далее, это условие может быть реализовано за счет использования техники искусственного согласования фаз. Сейчас же мы продемонстрируем преимущество (12.38) по сравнению с (12.27), Для этого мы умножим каждое уравнение в (12.38) на А* и прибавим к нему его комплексно сопряженное выражение. Тогда мы получим:
|
|
|
|
(12.40)
|
|
Это приводит к уравнениям Мэнли—Роу:
|
|
(12.41)
Уравнения Мэнли—Роу отражают тот факт, что поток фотонов сохраняется. Таким образом, в эксперименте с суммированием частоты фотоны с энергией Н со3 могут возникать только за счет числа образующих их фотонов с энергией Н сох и Н со2. Иначе говоря, соотношения Мэнли—Роу вскрывают асимметрию энергетического обмена. В случае процесса генерации разностной частоты (о){ = со3 — со. г) мы видим, что фотоны с энергией Нсо3 поглощаются и создаются фотоны с энергией Ьсо2 даже, если они уже присутствуют. Мы возвратимся к этому аспекту позже (смотрите раздел 12.8).
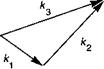
Таким образом, мы видим, что процесс преобразования частоты можно интерпретировать в рамках корпускулярного подхода. Фотоны с энергией Нсох, Нсо2, Ьщ не могут обмениваться энергией за исключением случаев, когда их энергия, как и импульс частиц сохраняются при взаимодействии (смотрите рис. 12.6):
|
|
(12.42)
Законы сохранения энергии и импульса для фотонов
Со
Рис. 12.6. Условия переноса энергии между тремя волнами сор со2, а)ъ во время взаимодействия в нелинейной среде могут интерпретироваться с использованием законов сохранения энергии и импульса, управляющих фотонами, образующими волны.
