Оптоэлектроника

Согласование фаз в режиме двулучепреломления

Многие кристаллические материалы (и среди них некоторые полупроводники) об­ладают анизотропными оптическими свойствами благодаря своей кристаллической структуре. В этом разделе мы ограничим наше рассмотрение одноосными кристал­лами — кристаллами, обладающими осью симметрии, относительно которой любая элементарная операция симметрии не приводит к изменению кристалла (напри­мер, поворот на л/3, п/4 и т. д.). Предположим для определенности, что эта ось (называемая оптической осью) лежит в направлении 01. Из элементарной теории оптики мы знаем, что такой кристалл является двулучепреломляющим, т. е. коэффи­циент оптического преломления не является одним и тем же параметром для всех направлений распространения. Говоря более точно, электромагнитная волна, рас­пространяющаяся вдоль оси 01 характеризуется коэффициентом преломления по (индекс «О» обозначает обыкновенную волну) тогда, как волна, распространяющаяся в любом другом направлении в плоскости Оху, характеризуется другим коэффици­ентом преломления пе (индекс «е» обозначает необыкновенную волну)

Более того, из оптики нам известно, что при любом направлении распростра­нения электромагнитной волны возможны лишь два главных направления поляри­зации, а именно: волна, поляризованная вдоль одного из этих главных направле­ний поляризации, останется линейно поляризованной во время своего распростра­нения через кристалл. Эти два главных направления геометрически определяются так, как это показано на рис. 12.Б.1. С этой целью рассмотрим эллипсоид коэффици­ента преломления, определяемый геометрическим местом точек (х, у, г), для кото­рых справедливо соотношение:

(12.Б.2)

Пусть распространяющаяся волна имеет волновой вектор к. Без потери общности мы можем предположить, что волновой вектор лежит в плоскости Оуь Пересечение плоскости, перпендикулярной к, с эллипсоидом коэффициента преломления дает нам эллипс (смотрите рис. 12.Б. 1). Две главные оси, одной из которых является ось Ох, и являются двумя главными направлениями поляризации, при этом величина двух главных осей этого эллипса дает коэффициент преломления для каждой поля­ризации. Из рисунка 12.Б.1 понятно, что коэффициент преломления вдоль оси Ох не зависит от угла в, и он всегда равен п это — обычная поляризация. С другой стороны, второе разрешенное направление поляризации (необыкновенная поляризация, соответ­ствующая волновому вектору к) характеризуется коэффициентом преломления пе, который зависит от угла в и определяется простым соотношением:

Со б2 6 $т26

+

Если обыкновенный коэффициент преломления п0 меньше необыкновенного ко­эффициента преломления пе, то эллипсоид будет узким по экватору и в этом случае кристалл есть положительный одноосный материал. В противоположном случае, когда п0 > пе(как это показано на рис. 12.Б.1) кристалл представляет собой отрицатель­ный одноосный материал.

Г

Ось распространения

Направление

Необыкновенного

Луча

У

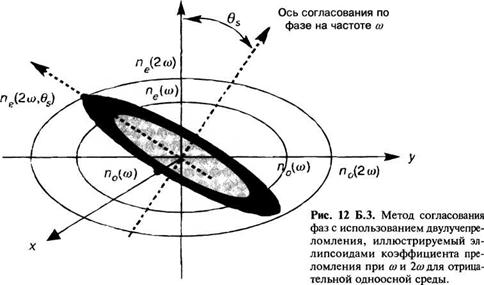
Рис. 12.Б.1. Определение двух разре­шенных направлений поляризации в среде с двулучепреломлением. Один из двух коэффициентов преломления (пе) зависит от угла в между волновым век­тором и оптической осью. Этот рису­нок соответствует ситуации в т. н. от­рицательной одноосной среде.

Фазовое согласование в режиме двулучепреломления использует эту оптическую анизотропию. В этом случае при определенных условиях можно обеспечить равенство коэффициента преломления п(со) в одном главном направлении и п(2со) в другом на­правлении. Говоря более точно, хотя в общем случае мы имеем п(2а), в) > п(со, в), мы можем, используя отрицательный одноосный материал, обеспечить:

Пе(2о>, в,)= «„(«)

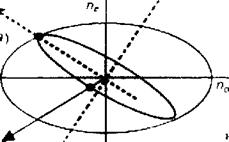
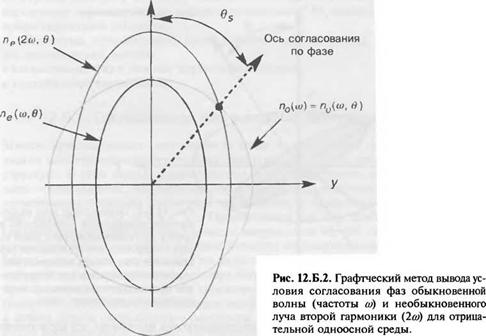
В случае положительного материала мы должны использовать по(2со) = пе(со, в). Для решения этого уравнения перейдем к плоскости Оу1 и попробуем найти угол 0, который удовлетворяет этому уравнению. Рассмотрим нормальный эллипс необыкно­венных коэффициентов преломления, образованный геометрическим местом точек М, для которых ОМ(в) = пе(а), в) и который дает сферу обыкновенных коэффициентов преломления, точки которой Мудовлетворяют соотношению ОМ(0) = по(а0). Рису­нок 12.Б.2 показывает, что нормальный эллипс коэффициентов преломления может быть получен из индекса коэффициентов преломления вращением на п/2. Добавим к этому рисунку нормальные эллипсоиды коэффициента преломления, соответствую­щие частоте 2а). Пересечение между сферой по(а)) и эллипсом пе(2а), в) задает конус относительно оптической оси, вдоль которого имеет место согласование фаз между волной со и ее второй гармоникой 2со (смотрите также рисунок 12.Б.3).

Понятно, что решение существует только тогда, когда по(со) > пе (2а>) > пе(со), т. е. при наличии существенного двулучепреломления. Используя равенства (12Б. З) и (12.Б4), мы видим, что угол вг определяется условием:

Или вновь:

(12.Б.6)

Режиме двулучепреломления

Это последнее уравнение позволяет прямо рассчитать угол фазового согласования, как только становятся известными дисперсионные соотношения для каждой поля­ризации. Большинство из них может быть получено из уравнений Зеллмайера (урав­нение (7.Б.2) или Афромовича (уравнение (7.Б. 10)) соответственно для широкозон­ных и узкозонных полупроводников. После того, как становится известен угол фазо­вого согласования, нам остается рассчитать величину квадратичной оптической восприимчивости с использованием уравнения (12.17). Понятно, что результат будет

Зависеть от различных ненулевых членов тензора ^2(2<у) и, таким образом, от симмет­рии кристалла. Читатель может найти описание всех соответствующих тензоров в справочном пособии по нелинейной оптике, таком как книга Сазерленда (1996).

Пример----------------------------------------------------------------------------------------------------------

Ниобат лития является одним из наиболее популярных нелинейно-оптических мате­риалов. Это не полупроводник, а скорее изолятор типа оксида металла, который обла­дает сильным двулучепреломлением и, таким образом, он хорошо пригоден для реали­зации фазового согласования. Обыкновенный и необыкновенный коэффициенты пре­ломления этого материала даются зависимостями типа соотношений Зелл майера:

В

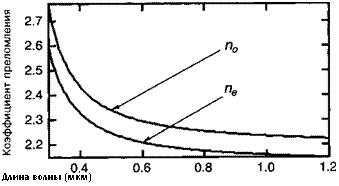
Рисунок 12.Б.4 иллюстрирует дисперсионные зависимости этого материала.

Мы хотим согласовать по фазе кристалл ниобата лития для того, чтобы добить­ся удвоения частоты излучения лазера на основе Nd: YAG на длине волны 1,3 мкм и получить световой пучок на длине волны 0,65 мкм. Таким образом, нам надо решить уравнение (12.Б.6). Приведенная ниже программа MATHEMATICA может быть использована для решения задач подобного рода.

Ае=4.820;Ье=0,099169;c=0.044432;de=0.021950;

Ao=4.9048;bo==0.117768;co=0/4750;do=0.027169; ne2[IJ:=ae - Ье/(се-Г2

Ne[l_ ]:Sqrt[ne2[l]

No2l ]::ао-Ьо/(со-Г2)- с! о*Г2

No(l_]:Sqrt[no2[l]]

Funct=(1 ./no2[l]-1 ./ne2[l/2]-1 ./n02[l/2]; thкta =ArcSin[Funct]*180/Pi;

N [thкta]/. 1/3

ParametricPlot[ {thкta, I}, {1,1.1,3.5}]

Рис. 12.Б.4. Дисперсионные кривые ниобата лития.

Фазовое согласование параметрических колебаний в режиме двулучепреломле - ния может быть реализовано с использованием тех же самых принципов. Однако в

Этом случае нам необходимо удовлетворить требования по сохранению как энергии, так и импульса фотонов. В случае пучка накачки на частоте соу а также сигнального и холостого пучков с частотами сох и со2 условия в (12.42) могут быть записаны в виде:

О), + 0)^ = со,

(12.Б.7«)

= Щ(0Ъ

Поскольку п1/п3 и п2/п3 меньше 1, оптическая дисперсия вновь будет препят­ствовать фазовому согласованию, если только с помощью какого-либо приема (на­пример, использования двулучепреломления) ее не удастся скомпенсировать. В от­рицательном одноосном материале (пе < п0) естественно выбирать конфигурацию, в которой сигнальная и дополнительная волны имеют обычную поляризацию, а волна накачки — необыкновенную поляризацию так, чтобы отношения п~(о)^/пе(а)^ и п0(со2)/пе(со3) делали два уравнения в (12.Б. 1а) совместимыми. Такая ситуация со­ответствует т. н. еоо-конфигурации, при этом:

1пМ)- = кЫ - по(щ)]щ (12.Б.76)

В этом случае оба члена положительны. Угол фазового согласования 0 определяет­ся уравнением:

П0{а)а +пЛ(о2)щ=пе(щ,^)оЬ

Здесь: изменение пе в функции 0 дается выражением (12.Б. З). Таким образом, за счет параметрического взаимодействия (или «расщепления») может быть получена любая частота сох в том случае, когда следующее выражение допускает решение 0(6^):

-1/2

(12.Б.9)

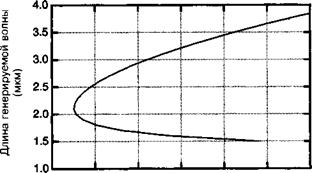
Рисунок 12. Б.5 демонстрирует изменение длины волны сигнальной и холостой волн в функции угла фазового согласования 0 для пучка накачки на длине волны 1,06 мкм в кристалле ниобата лития ЫМ)03. Возможны и другие конфигурации фазово­го согласования (например, еое, оео...), при этом заинтересованному читателю рекомен­дуется более детально ознакомиться со специальной литературой по этому вопросу.

Пример----------------------------------------------------------------------------------------------------------------------------------------------------

Диаграмма фазового согласования для нелинейного материала представляет собой набор пар (для сигнальной и дополнительной волн), которые могут генерироваться при заданной длине волны накачки в функции такого параметра, как угол 0 между

Рис. 12.Б.5. Угловая зависи­мость фазового согласования для ниобата лития на длине волны 1,064 мкм. (С разреше­ния Т. ОеЬшззсЬеЛОТНАЬЕБ).

Волной и оптической осью кристалла. Программа MATHEMATICA, приведенная ниже может быть использована для решения уравнения (12.Б.9) (дисперсионные кривые имеют тот же самый вид, что и в предыдущем примере)

Ае=4.5820;Ье=0.099169;ce=0.044432;de=0.021950; ao=4.9048;bo=0.11768;co=0.04750;do=0.027169; ne2[ij:ae-be/(ce-r2)-de*r2;ne[i ]:=Sqrt[ne2(i)]; no2[i ]:=ao-bo/(co-r2)-do*r2;no[l_]:=Sqrt[no2[i]]; lp=1.06; 12= 1./ (1./ip-1./i1); f1=((lp/l1)*no[M]+(lp/l2)*no[l2]''2; f2=1/f1-1/no2[ip]; f3= 1/ne2[lp]-1/no[lp];

Fctopo=Sqrt[f2/f3];theta=ArcSin[fctopo]*N[180/Pi];

ParametricPiot[ {thкta, i 1}, {H, 1.5,4.}]

При наличии средств для обеспечения фазового согласования в режиме двулу- чепреломления реализация оптического параметрического генератора (ОРО) как спектрально перестраиваемого источника когерентного излучения становится оче­видной (смотрите рис. 12.Б.6). Лазерный резонатор обеспечивает мощный пучок излучения с частотой а)у Этот пучок в дальнейшем претерпевает параметрическое взаимодействие с нелинейным кристаллом внутри резонатора с одиночным или двойным резонансом. Зеркала ОРО проектируются таким образом, чтобы обеспе­чить повышенный коэффициент отражения в требуемом спектральном диапазоне перестройки для сигнального и холостого пучков. Перестройка длины волны ОРО осуществляется поворотом кристалла с тем, чтобы найти угол фазового согласова­ния, требуемый для получения необходимой частоты сигнала сох (уравнение (12.Б.9)).