Оптоэлектроника

Поверхностные явления

На поверхности полупроводника нарушается периодичность кристаллического по­тенциала. Каждый атом на поверхности связан со стороны полупроводника с лежа­щими ниже атомами объема, тогда как электронные волновые функции с вакуумной стороны границы раздела являются несвязанными и распространяются в свободное пространство. Такие незавершенные поверхностные состояния называются свободны­ми связями. Эти два эффекта приводят к формированию электронных состояний в запрещенной зоне объемного материала вблизи поверхности (смотрите дополнение 5.Г). В действительности такие локализованные поверхностные состояния непре­
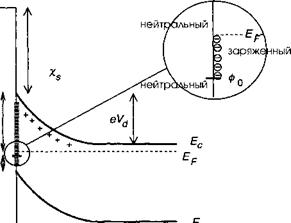
рывно распределены по запрещенной зоне и образуют в ней континуум. Для того, чтобы характеризовать этот континуум, введем характеристический уровень ф0 над потолком валентной зоны, который обладает следующим свойством: когда поверх­ностные состояния заняты вплоть до уровня ф0, поверхность является электрически нейтральной. С использованием полупроводниковой терминологии можно сказать, что состояния ниже ф0 ведут себя как доноры (поскольку они нейтральны, когда заняты электронами), тогда как состояния выше ф0 проявляют характеристики ак­цепторов (поскольку они становятся отрицательно заряженными, будучи занятыми электронами). В действительности поверхность всегда подвержена воздействию ок­ружающей атмосферы и очень вероятным является то, что примеси, адсорбирован­ные поверхностью будут давать свой вклад в заселенность локализованных состоя­ний в запрещенной зоне. Однако этот вклад может быть включен в определение ф0.

Например, на поверхности полупроводника л-типа проводимости положение уровня Ферми определяется легирующими примесями внутри материала. При тер­модинамическом равновесии положение уровня Ферми неизменно по всей струк­туре. На поверхности поверхностные уровни должны быть заполнены вплоть до уровня Ферми, что приводит к формированию поверхностного заряда:

<г = - еЫя[Е,-ф0-ЕАО%

Здесь ТУ, (см-2 эВ_1) есть плотность поверхностных состояний, которая для простоты пред­полагается здесь постоянной по зоне, а £(0)есть положение валентной зоны на поверхности (смотрите рис. 10.1).

Поскольку структура в целом нейтральна, этот поверхностный заряд должен быть ском­пенсирован пространственным зарядом в полупроводнике, распределенным по области обеднения (смотрите рис. 10.1). В противоположность поверхностному заряду, распреде­ленному в области толщиной порядка атомного монослоя, глубина обеднения Ь является макроскопической величиной. Падение электростатического потенциала в этой области пространственного заряда было описано в главе 6 и определяется уравнением (6.69):

(Ю.4)

Здесь сгесть заряд области обеднения. Таким образом, положение зоны проводимо­сти на поверхности составляет Ес(0) = Ес(°°) + е У^ и оно представляет собой внут­ренний потенциальный барьер, мешающий электронам покинуть объем полупро­водника. Падение потенциала можно получить подстановкой (10.4) в (10.3):

Вакуум	Полупроводник
Рис. 10.1. Поверхностные со­стояния между уровнем Фер­ми и ф0 создают поверхност­ный заряд, который компен­сируется пространственным зарядом в области обеднения.
■>

-LNS-£,(-)]

2 £

Или:

2

И, 1+ !£-£* ' 2 £

В пределе очень больших концентраций поверхностных состояний УЛ перестает зави­сеть от При этом уровень Ферми на поверхности становится, таким образом, фиксиро­

Ванным при £(0) + ф0 и его положение определяется выражением:

Ес (О ) ЕР - е Ус{ + Ес (о® ) ЕР - Е8 ф0

В этом случае толщина области обеднения равна соответствующей глубине обеднения для потенциала У^

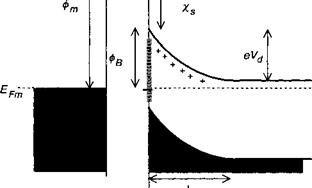
Проанализируем теперь поведение металлического слоя, осажденного на полупровод­ник. Сначала мы отметим, что прежде, чем электрон сможет покинуть полупроводники перейти в вакуум, электрон на дне зоны проводимости у поверхности должен преодолеть барьер д. Этот параметр называется электронным сродством полупроводника и он выража­ет энергию, удерживающую электроны в материале (смотрите рис. 10.2).

В качестве мысленного эксперимента представим себе, что мы придвигаем металл ближе к поверхности полупроводника. Поскольку металл не имеет запрещенной зоны, его сродство равно работе выхода из металла фт (т. е. разности энергии между уровнем Ферми и вакуумом). Если мы закоротим эти два материала внешним проводом, уровни Ферми выравнятся. Это произойдет вследствие переноса заряда между полупроводником и ме­таллом, что приведет к разнице потенциальной энергии между внутренними объемами двух этих материалов. В металле, обладающем колоссальным количеством свобод­ных электронов (1022—1023 см-3) перенесенный заряд ограничен в пределах поверх­ностного слоя с толщиной, определяемой длиной Дебая, называемой также длиной Томаса—Ферми в металлах. Поскольку в металлах эта величина крайне мала, этот поверхностный слой может быть представлен как поверхностный заряд.

Со стороны полупроводника распределение перенесенного заряда может быть описано с использованием двух моделей.

Металл вакуум полупроводник

Ферми. Распределение этого заряда определяет высоту барьера Шотки фг

1. Модель Шотки. В отсутствие поверхностных состояний заряд формируется только в пределах слоя обеднения. По мере того, как расстояние между двумя мате­риалами стремится к нулю, зона проводимости фиксируется на уровне:

ЕЛ0)=Фт~Х, (Ю. В)

Это уравнение означает, что на границе раздела нет заряда. При этом падение по­

Тенциала на области обеднения составляет:

ЕУл = £с(0)- £,(«) = фя-х,~ Е(~) (10.9)

Здесь: величина £(°°) определяется уровнем легирования. Это и есть модель Шотки.

2. Модель Бардина. В противоположном пределе, когда плотность поверхност­ных состояний велика, переносимый заряд может быть легко обеспечен за счет осво­бождения достаточного количества поверхностных состояний без существенного вли­яния на полупроводниковые зоны. В этом случае величина еУа полностью определя­ется ф0 и не зависит от типа осаждаемого металла. Это есть модель Бардина.

В рамках обеих моделей высотой барьера Шотки называется энергия:

Ефв = Ес{0)-Ег (10.10)

В рамках первой модели фв зависит от металла, но не от уровня легирования полу­проводника. В модели Бардина фв не зависит ни от металла, ни от уровня легирова­ния полупроводника.

На практике экспериментальные результаты соответствуют промежуточной между двумя моделями ситуации, при этом более часто они все-таки согласуются с моде­лью Бардина. Более того, после осаждения металла возможна модификация повер­хностных состояний за счет химической связи между двумя типами материалов, при этом как фв, так и ф0 начинают зависеть от металла. Суммируя изложенное, можно сказать, что высота барьера Шотки зависит от пары металл/полупроводник, но при этом указанная зависимость намного слабее той, которая предсказывается моделью Шотки. При последующем рассмотрении мы будем предполагать, что фв слабо зависит от пары металл/пол у проводник и не зависит от уровня легирования, при этом величины фв будут браться из эксперимента.

Как говорят, пара металл/полупроводник образует контакт Шотки к полупро­воднику. Мы увидим, что такой тип контакта действует как выпрямляющий контакт (т. е. обеспечивает преимущественное токопротекание в одном направлении), что является важной характеристикой, используемой в диодах Шотки. Такие же прибо­ры находят свое применение в качестве приемников оптического излучения.