Поле излучения осциллирующего заряда: калибровка Лоренца
Покажем теперь, каким образом уравнения Максвелла—Лоренца позволяют рассчитать мощность электромагнного поля, излучаемого осциллирующим зарядом. Такой расчет важен по нескольким причинам. Во-первых, с точки зрения исторической перспективы эта теория потерпела неудачу в попытке объяснить стабильность атома водорода и проложила еще один путь к формированию квантовой механики. Она продемонстрировала также внутреннюю связь между движением заряженных частиц и светом, что помогло Лоренцу, Пуанкаре и Эйнштейну встать на путь, ведущий к теории относительности. И наконец, зависимость мощности излучения от длины волны имеет и технические следствия там, где диффузный характер процесса имеет место, например в оптических волокнах, атмосферных процессах и т. д.
Рассмотрим заряженную частицу, расположенную в начале координат точке О и подвергнутую малому смещению ге(0 около точки О (см. рис. 2.А.1).
Вспомним уравнения Максвелла—Лоренца:
Точечный
Источник
|
Рис. 2.А.1. Расчет векторного потенциала точечного заряда
|
|
|
Вместо того чтобы использовать Фуре-преобразование, которое наилучшим образом подходит для рассмотрения плоских волн, мы попробуем отыскать дифференциальные уравнения, которым должны удовлетворять скалярный и векторный потенциалы. Для этого подставим (2.А. Зб) в уравнение Пуассона (2.А.1я), что дает:
Ч2и+^-(Ч А) = -^- (2.А.4)
Э? £0
Подобным же образом, вводя (2.А. За) и (2.А. Зб) в уравнение Фарадея—Ампера (2.А.1г), получаем:
|
V х (V х А) = — С2 |
Теперь применим классическое векторное тождество к А и V:
А х (Ь х с) = (а • с)Ь - (а • Ь)с (2.А.6)
Что позволяет записать (2.А.5) в виде:
|
-72А + ——А + У С2 Эг2 |
![]()
|
ЧА + — — и С2 Э/ |
![]() 1
1
(2.А.7)
Ос
Поскольку векторный потенциал определен с точностью до градиента потенциала, можно показать, что мы можем воспользоваться этой степенью свободы для введения калибровки, называемой лоренцовской калибровкой, в рамках которой векторный и скалярный потенциалы связаны друг с другом соотношением:
У-А^=0 (2.А.8)
1 с2 Э/
Лоренцовская калибровка
Эта калибровка особенно удобна для рассмотрения проблем излучения. В самом деле, (2.А.7) сильно упрощается, так как прямо связывает одиночный векторный потенциал А с движением заряда, создавшего его:
-У2А^— ^-Аг. =— * (2.А.9)
1 с2 д(2 1 е0с* ' ’
Решения этого дифференциального уравнения известны, соответствуют потенциалу задержки и могут быть записаны в виде:
'ГЛ1,2. АЛО)
Сделаем теперь несколько упрощающих предположений:
• смещение ге(0 частицы мало по сравнению с расстоянием наблюдения. Таким образом, при оценке векторного потенциала объем интегрирования может рассматриваться как точечный по отношению к расстоянию г.
• смещение источника мало в сравнении с длиной волны излучения, что является другим выражением условия, когда движение частицы является нерелятивистским.
В этом случае уравнение (2.А. 10) сразу упрощается:
А^г> ') = 7—Ц - [ /г'> * ~ -]с13г' (2.А. Ш)
Але„с2г ^ с )
Где г — амплитуда вектора г, что с учетом определения плотности тока точечного заряда (2.А.6) приводит к выражению:
|
А,(М) = 1 ^ Г/С) (2.А.116) 4 ле0с2 г Векторный потенциал, генерируемый движущимся зарядом Где Б(7) есть векторный диполь Б(7) = фе (/). Для полного определения электромагнитного поля мы должны еще рассчитать скалярный потенциал, задаваемый условием Лоренца (2.А.8): = - С*7 ■ А4 Теперь мы должны рассчитать дивергенцию 1>(7 — г/с)/г. С этой целью используем соотношение: |
|
X '7* .Л А*3 Гъ |
|
|
|
|
|
Ъц-г/с) |
|
£Мг, 0 = |
|
4 жє0г2с |
|
|
4 яє0с2 |
|
Ух |
|
1 |
|
1>(/- г/с) + і V х й(/- г/с) |
|
— к! Ч?-г/с)——— х 1)(/ — г / с) Гъ сг2 |
|
(2.А.15) |
|
1 |
|
Гхй(/ - г / с) (2.А.16) Магнитное поле движущегося заряда Расчет электрического поля осуществляется аналогичным образом, но требует несколько больших усилий: |
|
В(г, о = - |
|
4 7Г€0С3Г2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
 |
|
|
|
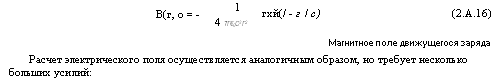 |
|
А*2 |
|
Г-ІХ/т/с),^, / • А*3 СА*3 |
|
Ї)(/-А*/с)Г, |
|
1 Р(/-г/с) ( г________ Г 4тте0с сгъ |
|
1 |
|
Лтсе0с2 |
|
|||
|
|||
|
|||
|
|||
|
|
||
Что в конце концов дает:
|
(2.А.18*) |
|
А*3 |
|
Е(г, г) = - |
|
1 гх[гхЙ(/ - г/с)] |
|
4л20с2 |
|
1 а±(/-г/с) |
![]() Или, как это было получено Рэлеем:
Или, как это было получено Рэлеем:
|
(2.А.186) |
![]() Е(г, /) = -
Е(г, /) = -
Электрическое поле движущегося заряда
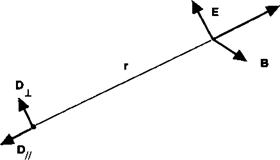
Где — компонента вектора диполя, перпендикулярная направлению точечного источника (рис. 2.А.2). Заметим, что амплитуда излучаемого электрического поля совпадает с расстоянием 1 /г, а не 1/г2, что характерно для статического поля точечного заряда. По этой причине радиоволны обладают существенно большим диапазоном распространения по сравнению с электростатическим полем — этот результат восхитил Герца и привел, в конце концов, к развитию радиосвязи. К следствиям этого мы возвратимся позже. Как известно, электрическое и магнитное поля перпендикулярны друг другу и по отношению к вектору распространения г. Говоря более точно, они связаны друг с другом соотношением:
В(г,0 = - ГХ-Е(Г, Г) (2.А.19)
С г
Поток энергии, излучаемой точечным зарядом через единицу площади в единицу времени, дается вектором Пойнтинга в:
|
(2.А.20) |
![]() В(г,0 = — ЕхВ = — Ех(гхЕ) = — [£2г-(Е г)Е] Мо Моге цйгс
В(г,0 = — ЕхВ = — Ех(гхЕ) = — [£2г-(Е г)Е] Мо Моге цйгс
|
В |
![]()
|
Рис. 2.А.2. Электромагнитное поле, излучаемое точечным зарядом |
![]() Поскольку Е и г перпендикулярны друг другу, уравнение (2.А.20) может быть записано в виде:
Поскольку Е и г перпендикулярны друг другу, уравнение (2.А.20) может быть записано в виде:
-Ч (2.А.21)
4 jcEqC* 4кг
Поток энергии через единицу площади в единицу времени, излучаемой движущимся точечным зарядом
Где ur — единичный вектор в направлении точечного источника. Выражение (2.А.21) содержит обильную информацию. Можно представить себе поток излучаемой энергии как будто истекающим из точечного источника со скоростью света при сохранении полной величины, проинтегрированной по поверхности сферы радиусом г и с центром в источнике.
Применим теперь этот общий результат к частному случаю заряда q9 движущегося синусоидально вдоль оси Oz. В этом случае вектор диполя дается выражением:
D±(r, t) = qa cos(cot)ez (2.A.22)
При этом вектор Пойнтинга принимает вид:
S(r, t) = gW, cos’.fl*rin».gJL. (2.А.23)
4ле0с34лг2 4 яг2
Поток энергии, усредненный по нескольким периодам, дается соотношением:
GW sin^
32 /Г2£0С3 г2
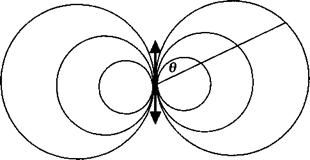
Ансамбли этих точек постоянной энергии (таких, для которых sin в /г остается неизменным) расположены вдоль окружностей, касающихся осциллирующего диполя (см. рис. 2.А. З).
Из-за того, что излучение диполя является достаточно направленным, интенсивность поля спадает как 1 /г, а не как 1/г2.
Мощность, излучаемую через поверхность сферы с центром в осциллирующем заряде, можно получить, оценивая интеграл по поверхности от (2.А.24), что дает:
(2.А.25)
32я! е0с} J г>
Г - const
Или после интегрирования:
12яе0с3
Полная мощность излучения осциллирующего диполя
|
|
|
Рис. 2.А. З. Поверхности постоянной энергии излучающего диполя |
|
|
Это выражение также содержит богатую информацию. Оно, например, показывает, что мощность излучения осциллирующего диполя пропорциональна четвертой степени частоты. Таким образом, голубой свет (Л » 0,4 мкм) рассеивается атмосферными частицами примерно в шесть раз сильнее, чем красный свет (Л « 0,65 мкм). Это объясняет, почему небо голубое, а закат кажется окрашенным в красный цвет, а также почему голубая неоновая реклама формирует яркое гало туманными вечерами. Говоря более прозаически, оно дает основу метода расчета времен жизни электронов на атомных уровнях.
То, что (2.26) говорит нам, заключается в следующем: электроны теряют свою энергию из-за электромагнитного излучения, и их движение в конце концов должно прекратиться. Природа этого эффекта заключается в работе, совершаемой движущейся заряженной частицей в электромагнитном поле, которое она сама создала! Для описания этого эффекта введем в выражение для диполя член трения ук (равный /тю где тк — излучательное время жизни), соответствующий радиационным потерям:
|
(2.А.27) |
![]() Ті + т ук1 + тсо2і = 0
Ті + т ук1 + тсо2і = 0
Мы знаем, что если тк » 1/я>, решения для описания движения принимают вид
I =асо$М е"'/2г, при этом энергия частицы уменьшается как Ее~‘/Т*. В этом случае тя дается соотношением:
|
Р гп <, пі и/ - С Г; =-------------------- ~ 2 2 |
|
Ті2 т(о2і2 |
|
Тсо2а2 2 |
|
|
|
|
|
|
![]()
Таким образом, мы получаем излучательное время жизни осциллирующего электрона, окружающего атом:
|
(2.А.30) |
![]() 6 яє0с3т д2о)2
6 яє0с3т д2о)2
Излучательное время жизни электрона, осциллирующего с частотой со
Что, будучи выражено через длину волны, дает:
|
|
(2.А.31)
Излучательное время жизни электрона, излучающего электромагнитную волну с длиной волны Л
Выражение (2.А.31) позволяет нам понять отчаяние физиков в конце девятнадцатого века. Поскольку, как представлялось, электроны орбитально вращаются вокруг атомных ядер с частотами порядка 1015 Гц, выражение (2.31) показывает, что все они должны тормозить до остановки и, в конце концов, разрушаться на ядрах после нескольких наносекунд. Как мы увидим в главе 3, квантовая механика позволяет нам разрешить этот исторический парадокс. Тем не менее, уравнение (2.31) оказывается достаточно надежным в предсказании времен жизни для излучательных переходов в лазерах. Ниже приводятся два типичных примера:
Л = 1 мкм, т = 45 не Л = 10 нм, т = 4,5 пс
Таким образом, намного легче аккумулировать электроны в возбужденных состояниях, подверженных инфракрасным переходам, чем заселить уровни, веду-
2. Б. Тепловидение
![]() Щие к проявлению рентгеновского излучения. И в результате, как мы увидим позже, реализация инфракрасных лазеров намного проще, чем в случае рентгеновских лазеров.
Щие к проявлению рентгеновского излучения. И в результате, как мы увидим позже, реализация инфракрасных лазеров намного проще, чем в случае рентгеновских лазеров.
Пример-------------------------------------------------------------------------------------------------------------
Уравнение (2.А.26) является очень ценным инструментом для расчета оптической мощности, излучаемой точечным источником, т. е. в случае, когда эффекты распространения не принимаются во внимание. В качестве приложения определим полную мощность излучения с удвоением частоты (2со) в нелинейно-оптическом материале, освещаемом фотонами с частотой со.
Пусть р будет атомной плотностью нелинейно-оптических центров (м_3), с! —нелинейной восприимчивостью (м/В), а ра — плотностью мощности падающего оптического излучения (Вт/м2). Нелинейный дипольный момент связан с коэффициентом d (смотрите главу 12) соотношением:
Дар = е0<1Е* = 2г0е0с1рш (2. А. 32)
Полная мощность Р2ф излучения с удвоением частоты (2со), преобразуемого рУ рассеивающими центрами (V— объем, на который сфокусировано первичное излучение), дается (2.А.26), а именно:
Л„ = руЩ^т~р1 (2.А. ЗЗ)
3 7Г£0С5
Так, что:
_^ = 2 (2 А 34)
V Зле0с5р
В случае ниобата лития с1 = 17пм/В, р — 1022 см-3, длины волны Л = 1,06 мкм и мощности первичного излучения 100 МВт/см можно найти, что мощность излучения на длине волны 532 мкм, излучаемого по всем направлениям, составит 1,4 мкВт.