Оптоэлектроника

Модель почти свободных электронов

В этом разделе мы представляем первый подход к теории зонной структуры, основанный на возмущении модели свободных электронов и называемый моделью почты свободных электронов. Используем уравнение Шредингера для электронов в периодическом одномерном кристалле с периодом решетки а (держа в уме, что обобщение этого рассмотрения потребует лишь мужественного привлечения соот­ветствующих индексов). Периодичность кристаллического потенциала в этом слу­чае делает его пригодным для Фурье-анализа:

(5.А.1)

Reciprocal

Lattice

Где, как мы напоминаем, векторы в принадлежат обратной решетке, т. е. они име­ют вид <7 = (целое число) х 2к/а. С использованием этих параметров уравнение Шредингера для потенциала приобретает вид:

Н¥(х) =

Волновая функция |/ (х) может быть также представлена в виде ряда Фурье за счет использования цикличных граничных условий Борна—фон Кармана ~К= п2я/(Ма), где Л/д относится к полной протяженности кристалла и п положительное (или нуле­вое) целое число — так что:

(5.А. З)

Подставляя (5.А. З) в (5.А.2), мы находим:

Теперь давайте умножим это уравнение на e~ikx и проинтегрируем по всему объему кристалла. Единственными ненулевыми членами будут те члены, для которых G — К = к. Это означает, что если в сумме появляется член к, то появятся и все другие векторы, являющиеся результатом прибавления к нему одного или нескольких векторов обратной решетки G (смотрите рис. 5.А. 1). Таким образом, в качестве индекса вол­новых функций мы можем использовать волновые векторы к, выбираемые произ­вольно в пределах первой зоны Бриллюэна, что позволяет записать собственные функции в виде:

-i(A-G)x

Г*(*)= -<7)

Это есть ничто иное, как теорема Блоха—Флоке. В этом случае применение уравне­ния Шредингера (5.А.2) к блоховским функциям у/к приводит его к виду:

I'|C(*)+5VcC(*-G)=0

2т

Это есть секулярное уравнение по С(к — б), обладающее нетривиальными ре­шениями (т. е. ненулевыми решениями) только в том случае, когда детерминанат

Рис. 5.А.1. Точки, показанные на этом рисунке, представляют волновые векторы к, допускаемые цикличными граничными условиями Борна — фон Кармана для кристалла длиной L = 20 д, где а — постоянная решетки. Если член (к = —8 на этом рисунке) появляется в сумме (5.А.4), все остальные члены к + 2пп/а также будут включены.

Этой линейной системы равен нулю. Ранг этого детерминаната равен числу точек в обратном пространстве. Могло бы показаться, что мы мало продвинулись по срав­нению с исходным видом уравнения Шредингера, если бы мы просто заменили дифференциальное выражение на алгебраическое. Теперь примем гипотезу, что функция является сильно периодической, т. е., что она обладает таким малым числом Фурье-компонент, что мы можем рассмотреть единственную компоненту, что име­ло бы место для чисто синусоидального потенциала. Часть секулярного уравнения в (5.А.6) в этом случае может быть записана в виде:

(5.А.7)

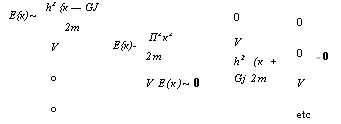Для каждого волнового числа к секулярное уравнение является полиномом Е (к) одного порядка с матрицей (таким образом имеется столько возможных реше­ний, сколько рядов содержит матрица). Эти решения непрерывны по к и таким обра­зом образуют энергетические зоны. Особенно интересный случай имеет место, когда к располагается вблизи границы зоны Бриллюэна, т. е. при к « 6/2 = п/а. В этом случае (7 — к и к имеют одну и ту же величину, при этом диагональные элементы подматрицы форматом 2x2:

H2G2 8/я

H2G2

Е{к)~

8 Т

Идентичны. Взаимодействие с ближайшим членом V снимает вырождение двух невозмущенных уровней Е(к) — h2G2/Sm. Это означает, что энергетические зоны, которые в другом случае обладали бы той же самой энергией при к = <7/2, стано­вятся невырожденными — теперь исследуем этот эффект более детально. Побли­зости от к = G/2 в детерминанте (5.А.7) доминирует подматрица формата 2x2 вблизи к = G/2, при этом уравнение для снятия вырождения приобретает вид:

(5.А.11)

Таким образом мы видим, что чем меньше ширина запрещенной зоны 2 V, тем меньше и эффективные массы. Такая же связь устанавливается и в рамках других моделей. Узкозонные полупроводники (исключительно пригодные для детектиро­вания инфракрасного излучения), как правило, характеризуются малыми эффек­тивными массами электронов и дырок.