Лазерный порог
Полупроводниковый р—«-переход, возбужденный до уровня выше порога прозрачности, будет способен усиливать те электромагнитные моды (т. е. фотоны), которые удовлетворяют критерию Бернара—Дюррафура. Как это описывалось в разделе 4.4, в среде будут наблюдаться лазерные колебания, если в ней обеспечены условия обратной оптической связи. Существует ряд методов, обеспечивающих необходимую обратную связь, которые описаны в дополнении 13.А. Простейший из них заключается в использовании естественного зеркала в виде границы полупроводник/воздух. В этом случае полупроводниковый резонатор получают скалыванием полупроводникового кристалла в двух различных местах вдоль той же самой кристаллографической плоскости, что обеспечивает идеально параллельные зеркала (смотрите рис. 13.13). Граница раздела полупроводник/воздух обеспечивает диэлектрическое зеркало с коэффициентом Ят, определяемым соотношением:
|
|
|
|
|
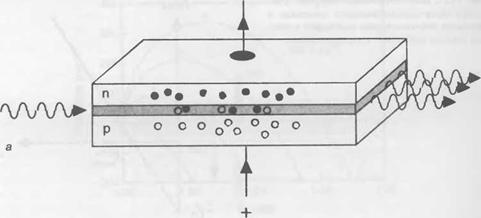
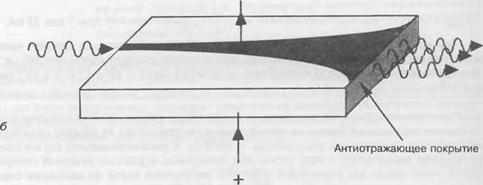
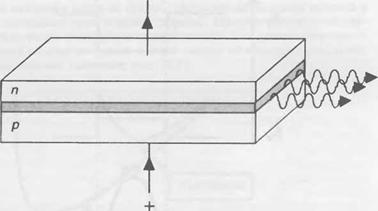
Рис. 13.12. Функционирование оптического полупроводникового усилителя (80А). Падающая волна, например, от выходного лазерного диода, усиливается прямосмещенным переходом (а). Одной из проблем при проектировании 80А является необходимость получения прибора с высоким усилением без режима собственной лазерной генерации. С этой целью для предотвращения возможности формирования стационарных оптических мод на длине волны усиления используются антиотражающие покрытия и рупорная геометрия прибора. |
В случае ваАБ, пх = 3,6 и коэффициент отражения составляет = 0,32. Эта величина может показаться малой по сравнению с параметрами зеркал, используемых в других типах лазеров (например, в газовых, ионных лазерах,...). Однако усиление, обеспечиваемое полупроводниковыми лазерами (вплоть до нескольких тысяч см-1), представляется значительным по сравнению с уровнями, обеспечиваемыми альтернативными лазерными средами. И как результат этого, использование сильно отражающих зеркал не является обязательным требованием для наблюдения лазерной генерации в полупроводниковых приборах. Физическую природу такого большого усиления в полупроводниках можно вскрыть, сравнив выражения для усиления в конденсированной (/?.(/*у)(£ —/)А2/8л;тк) и атомной (^Иу)(И2 — Ых)Л2/%л;т^ средах:
• Концентрация имеющихся центров излучения (несколько 1018 см-3) намного превосходит уровни, достижимые в газовых средах (1015 см-3).
• Оптические поперечные сечения также намного больше для электронов в зонах по сравнению с электронами на атомных орбиталях. Таким образом, на длине волны ~ 1 мкм в ионных или газовых лазерах типичное излучательное время жиз-
|
|
|
Рис. 13.13. Конфигурация полупроводникового инжекционного лазера с двумя зеркалами, полученными скалыванием. |
Ни составляет величину порядка 1 мс, в то время как в полупроводниках этот параметр составляет величину порядка нескольких наносекунд. Это связано с де- локализованной природой электронов проводимости в конденсированной среде.
В разделе 4.4 мы видели, что лазерные колебания возникают, когда усиление усиливающей среды стремится превысить резонаторные потери в оптическом резонаторе.
Имеется несколько типов потерь:
• Собственные потери ат как следствие потери фотонов при прохождении через зеркала (до некоторой степени необходимые, так как свет должен иметь возможность покинуть резонатор!). Это описывается соотношением (4.216) в виде:
= ~~ 1п _ ^ (13.24а)
2Ь
Здесь мы допустили возможность того, что зеркала имеют различные коэффициенты отражения (Ят1 и Ят2). В случае, когда одно из зеркал является полностью отражающим, порог генерации уменьшается. Ь есть длина резонатора.
• Паразитные потери а как результат поглощения свободных носителей в контактных слоях, вследствие рассеяния на шероховатости поверхности и т. д.
В этом случае условие достижения лазерного порога (4.21 б) принимает вид:
1 1
(13.246)
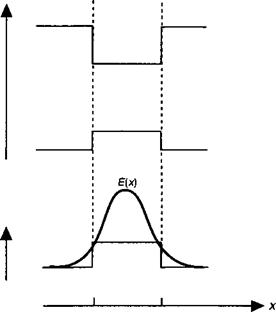
Это последнее выражение не учитывает тот факт, что усиленные моды (фотоны) должны удовлетворять уравнениям Максвелла в гетеропереходе. Соответственно такая структура ведет себя как волновод. В двойной гетероструктуре потенциальные барьеры, обладающие большей шириной запрещенной зоны по сравнению с квантово-размерным материалом, характеризуются меньшим коэффициентом преломления так, что электромагнитные волны остаются захваченными в среде с большим коэффициентом преломления (и, что более важно, остаются в области усиления — смотрите рис. 13.14)). В главе 9 (мы видели, что электромагнитное поле ограничено в структуре вдоль оси Ох, перпендикулярной к границам раздела, и что коэффициент распространения /? зависит от индексов поперечной моды (смотрите, например, (9.13)). Доля энергии, эффективно присутствующей в области усиления, дается коэффициентом ограничения Г (9.27):
|
|
|
П |
|
-с/ |
|
0 |
|
Рис. 13.14. Электронно-дырочная рекомбинация имеет место в области с наименьшей шириной запрещенной зоны и соответственно с наибольшим коэффициентом преломления. Таким образом, помимо обеспечения усиления, узкозонный полупроводник является также и областью оптического ограничения для усиленных оптических мод. |
|
(13.25) |
||£(х)Г<к
______
||£(х)Г<к
Таким образом, только доля Г электромагнитной энергии испытывает усиление (смотрите также раздел 8.7.2) в предположении, что как барьеры, так и ямы характеризуются теми же самыми потерями. Таким образом, выражение для лазерного порога модифицируется и приобретает вид:
Пороговое условие для лазера с гетеропереходом
Сконцентрируем теперь наше внимание на максимальном усилении, определяемом (13.22а). Это последнее выражение может быть представлено в более четком виде с использованием плотности порогового тока /1Нгс8Но1(1:
|
1 1 [28] Ап + —— 1п ——— Р 2Ь Ят1Ят |
|
Го |
|
Дс1пи |
|
|
 |
|
Поскольку коэффициент ограничения Г падает с уменьшением толщины двойной гетероструктуры с1 (смотрите (9.30), мы видим, что существует оптимальная
|
Тг = ■ |
|
1 |
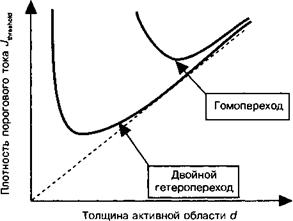
Величина с1. Эта ситуация иллюстрируется рисунком 13.15 в сравнении с аналогичной зависимостью для лазерного диода на основе гомоперехода. Большая разница в величине плотности порогового тока, с одной стороны, является результатом слабого оптического ограничения в лазерах с гомопереходом, а с другой стороны — результатом уменьшения объема материала в более тонких гетероструктурах, который должен быть инвертирован (смотрите рис. 13.2).
|
Рис. 13.15. Зависимость плотности порогового тока от толщины активной области </. По своей природе гетеропереходы характеризуются более низкой плотностью порогового тока вследствие лучшего перекрытия оптической моды и среды усиления, а также вследствие усиленного ограничения носителей. |
Пример-----------------------------------------------------------------------------------------------------------
Рассмотрим лазерный диод с гетеропереходом на основе ОаА8/А1хСа1 _х Ав с толщиной с1 ямы 100 нм. Излучательное время жизни составляет 5 не, а внутренняя квантовая эффективность у порога равна 50%. Резонатор диода имеет длину и ширину соответственно 500 и 5 мкм, а также полностью отражающее зеркало. Содержание А1х в барьерах достаточно велико, чтобы обеспечить коэффициент ограничения Г = 1. В этом случае потери на зеркале ат составляют:
Ат = 1п(1 /0,32)/(2х5х 10'2 см)= 11,4см-'
Предположим, что паразитные потери ар составляют 10 см-1, что приводит к аш = 21,4 см-1. Система перейдет в режим лазерной генерации, как только максимальное усиление утах в прямо смещенном диоде превысит а1о1. Применительно к рис. 13.10 это соответствует плотности порогового тока «/1Нге5Ьо1а= 800 А см-2 (или с учетом площади поверхности прибора пороговый ток /Шге8Но1с, составит 20 мА).
