Лавинный пробой
Если электрическое поле, приложенное к полупроводнику, значительно превышает поле скорости насыщения, часть из электронов будет способна приобрести дополнительное количество энергии по отношению к минимуму зоны проводимости, большее ширины запрещенной зоны Eg. В этих условиях становится возможным процесс ударной ионизации. Электрон взаимодействует со всеми другими электронами в валентной зоне за счет элекгрон - электронного взаимодействия, при этом он может возбудить через запрещенную зону другой электрон, что соответствует генерации электронно-дырочной пары (процесс генерации). В этом процессе сохраняются энергия и квазиимпульс. Перед столкновением мы имеем электрон в состоянии к. с энергией Ес(к.) и электрон в состоянии - кл с энергией Ev (кА). После столкновения в зоне проводимости имеются два электрона в состояниях kj и к2 при этом законы сохранения могут быть записаны (смотрите обратный процесс на рис. 6.Г. 1):
' л 1 ^ (6.В.1)
Ес( к,) + ЕД кл) = Ес( к,) + Ес( к2)
|
Кл |
![]() Для того, чтобы определить энергетический порог этого процесса, используем аппроксимацию параболической зоны Ес(k.) = Eg + h2k2/2me и Ev(kh) = ~h2kh2/2mh, а также предположим, что эффективные массы составляют для электронов те и для дырок т.
Для того, чтобы определить энергетический порог этого процесса, используем аппроксимацию параболической зоны Ес(k.) = Eg + h2k2/2me и Ev(kh) = ~h2kh2/2mh, а также предположим, что эффективные массы составляют для электронов те и для дырок т.
H2k2 г h2k? %2kl ti2k?
---- — - Е +------- — +---- — +---- -
2 то 8 2т, 2т„ 2т,
Мы можем убедиться в том, что минимум начальной энергии реализуется, когда все импульсы ориентированы в одном и том же направлении. Более изящно можно определить этот минимум (с использованием метода Лагранжа), минимизируя функцию:
/■ = £ +1*1- + 1*г - + 1**-+А(*1+Л2 + Л,) (6.В. З)
2 те 2 те 2тИ
|
Х _ К _к2 _ К Ь2 т. тс т, |
![]() Где Я есть множитель Лагранжа. Беря производную от к{, к2 и &й, мы находим, что:
Где Я есть множитель Лагранжа. Беря производную от к{, к2 и &й, мы находим, что:
(6.В.4)
Отсюда мы определяем минимальную начальную энергию:
|
= (б. в.5) 1+ 0»,/тп) |
![]()
|
2 т. |
![]() Ь7 к'
Ь7 к'
Это выражение приводит к порогам ударной ионизации слегка выше Е в случае тяжелых дырок, но к величине порядка 3/2Е в том случае, когда те, тИ близки друг другу. Таким образом порог ниже в случае генерации тяжелых дырок.
Из соображений симметрии аналогичный процесс, при котором начальной частицей является дырка, дает тот же самый результат, что и в предыдущем случае при соответствующей замене те на тк. В то же время мы должны четко представлять, что в рассматриваемом диапазоне энергии использование параболического приближения не является достаточно корректным.
Как только первичный электрон генерировал электронно-дырочную пару, он будет вновь ускоряться электрическим полем, что делает возможным его участие в последующих актах генерации пар. Подобным же образом после достаточного ускорения в электрическом поле каждая из вторичных частиц, в свою очередь, будет способна играть роль первичных частиц и участвовать в процессе генерации пар. Основным результатом такого процесса является то, что полная концентрация свободных носителей в структуре возрастает геометрическим образом. Такая ситуация в полупроводнике называется пробоем и сопровождается возрастанием концентрации свободных носителей и увеличением проводимости. На практике, мы определяем коэффициенты ионизации ап и ар (которые в дальнейшем будем полагать равными) как число вторичных пар, генерированных первичным электроном при пробеге электроном 1 см среды в направлении приложенного поля. Естественно, что эти коэффициенты зависят от напряженности поля Е. Таким образом, при перемещении через область сильного поля 0 < х < первичный электрон сможет генерировать:
И>
= |а/1(7г)/х (6. В.6)
Вторичных пар. Вторичные и последующие частицы могут генерировать полное число электронов в этой области (до тех пор, пока ТУ < 1), определяемое соотношением:
Nw= + N, + N,2+ М? +... = (6.В.7)
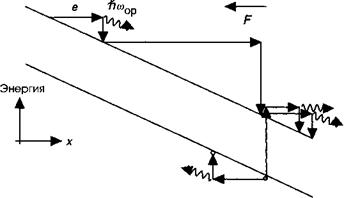
Если электрон входит в область при * = 0, на выходе из области при х = будет электронов. Мы определяем коэффициент умножения Мп для электронов как отношение выходного тока и тока на входе в область сильного поля. Аналогичным образом мы можем определить Мр для дырок как у (0) = Л/уДи^, где дырки входят в область в точке и> и покидают ее в точке 0. Рисунок 6.Ь.1 иллюстрирует явление лавинного пробоя.
Наиболее простая модель для определения коэффициентов ионизации предложена Шокли, и она известна под очаровательным названием модели счастливого электрона. Поскольку лишь электроны, которые обладают энергией больше пороговой, определяемой (6.В.5), будут способны запустить лавинный механизм, таких электронов будет очень немного, так как по большей части электроны будут растрачивать свою энергию в столкновениях еще до того, как из-за ускорения они приобретут пороговую энергию. Обозначим через Лор длину свободного пробега электрона до столкновения с оптическим фононом (для простоты предположим, что она не зави-
|
|
Рис. 6.В.1. Иллюстрация процесса умножения носителей за счет ударной ионизации. Под влиянием сильного приложенного поля У7 в область сильного поля в точке л: = О входит одиночная частица, в то время как Мп электронов выходят из области сильного поля.
Сит от энергии), а через Л обозначим среднюю длину свободного пробега до соударения с другим электроном (в предположении, что пороговая энергия уже достигнута). Наконец, предположим, что каждое столкновение сопровождается падением скорости электрона до нуля. Для того, чтобы приобрести пороговую энергию £., электрон должен пройти минимальное расстояние хР определяемое Е. = еЕх.. Вероятность того, что электрон сможет сделать это без рассеяния на оптических фононах составляет:
|
/ Л X: |
Е' ) |
||
|
Ехр |
Н |
= ехр |
1 |
Как только кинетическая энергия электрона превысит порог ионизации (смотрите рис. 6.В.2), средняя длина свободного пробега А будет определяться совместным проявлением двух механизмов 1/Я = 1/Л. + 1 /Л. Вероятность того, что первым актом столкновения, испытываемого электроном, является ударная ионизация (а не рассеяние на фононе решетки) составляет таким образом А/А.. Если же первым процессом будет столкновение с фононом, скорость электрона упадет до нуля, и он должен будет вновь наращивать энергию с самого начала. Для такого «холодного старта» вероятность ионизации будет составлять:
|
Рис. 6.В.2. Модель Шокли для определения коэффициента ионизации а первичный электрон приобретает энергию, достаточную для создания вторичной электронно-дырочной пары. |
|
|
|
(6 В.9) |
![]() О Я
О Я
|
ЕРАпг |
![]() Р( = — ехр
Р( = — ехр
|
(6.В.10) |
![]() Если мы определим аор как число столкновений с фононами на длине пробега в 1 см, баланс между энергией, передаваемой электрическим полем, и энергией, рассеиваемой в процессах ионизации и излучения фононов, может быть записан в виде:
Если мы определим аор как число столкновений с фононами на длине пробега в 1 см, баланс между энергией, передаваемой электрическим полем, и энергией, рассеиваемой в процессах ионизации и излучения фононов, может быть записан в виде:
ЕР = апЕ{ + аорЕор
Где а есть коэффициент ионизации, который мы ищем. В этом случае число актов набора энергии электронами из состояния остановки (после соударений) составляет ап + ар, что дает число столкновений на длине в 1 см:
№ (6В11)
Устраняя аор в (6.В.10) и (6.В.11), получаем:
|
ЕРР, |
![]()
|
(6.В.12) |
![]() ЕРРі
ЕРРі
Осп =
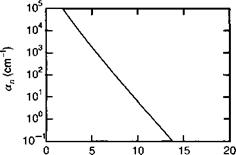
Где мы воспользовались тем фактом, что Е ор<< Е. (~50 мэВ и ~1 эВ соответственно). Повторная подстановка (6.В.9) в этом случае дает окончательный результат, иллюстрируемый рисунком 6.В. З:
|
(6.В.13) |
![]() ЕЕ ехр [- {Е, / еЕЛ00 )] (Я,/ЯКр + Е, ехр [- {Е, / еЕЛор )]
ЕЕ ехр [- {Е, / еЕЛ00 )] (Я,/ЯКр + Е, ехр [- {Е, / еЕЛор )]
|
Е11ерЛор Рис. 6.В. З. Зависимость коэффициента ионизации ап от напряженности приложенною поля в соответствии с уравнением (6.В.13) для кремния. Е. = 1,8 эВ, Лор = 10 нм, А. =200 нм. |
За исключением случаев очень сильных полей Р мы можем пренебречь вторым членом в знаменателе, что позволяет нам переписать (6.В. 13) в виде:
|
Е, ЕРЯ„, |
![]()
|
- еР ехр |
![]() (6.В.13)
(6.В.13)
Коэффициент ударной ионизации
Несмотря на крайнюю упрощенность этой модели выражение (6.В. 14) успешно воспроизводит экспериментально наблюдаемые зависимости ап от напряженности приложенного поля.
|
|
J. S. Blakemore, Semiconductors Statistics, Dover, New York (1987).