Квантовая яма. Общий случай
Рассмотрим теперь электрон в поле потенциала, изображенного на рис. 1.1, а именно потенциала, задаваемого соотношениями:
V (х) =0, если |*| > ~2
(1.31)
У(х) = - К0, если |*|<§
|
500 |
- |
||||
|
400 |
- |
||||
|
Со |
300 |
V |
------ |
||
|
Со |
|||||
|
О; £ И. А |
200 |
- |
£ |
||
|
Ш І Со |
100 |
- |
|||
|
0 |
1.1, |
І |
, і. і. |
||
|
-20 |
-10 |
0 |
10 20 |
|
-а/2 а/2 |
Положение (нм)
Рис. 1.1. Одномерная квантовая яма. Представлены собственные энергии и волновые функции для трех связанных состояний системы. Такие квантовые ямы, реализуемые в системе СаАз/А10 45Са0 55Аб. Интервал между первыми двумя энергетическими уровнями составляет 104 МэВ, что приводит к поглощению фотонов на длине волны 11,9 мкм.
Первая область (|х) > а/2) задает потенциальный барьер, тогда как вторая область (И < а/2) определяет яму. Уравнение Шредингера, определяющее поведение электрона в этой структуре, записывается в виде:
|
|
(1.32)
Сначала мы ищем решения этого уравнения с энергиями менее высоты потенциального барьера, т. е. Е < 0. Для этого мы вводим три величины к, к и к0 с размерностью обратной длины, т. е. имеющие размерность волнового вектора (число пространственных периодов в 2 /г), определяемые следующим образом:
2тр
|
(1.33) |
![]() Н2к
Н2к
У0 + Е = -
|
2т
|
Отметим, что величина 2/гД0 есть длина волны де Бройля, связанная с энергией У0 ограничивающего потенциала. С использованием этого обозначения можем записать решения уравнения (1.32) в общем виде как:
|
У/с(х) = Ассікх + Всс~[кх, для |х| < ^
|
(1.34)
|
|
Где символы с, / и г обозначают соответственно центральную, левую и правую области. Теперь проиллюстрируем процесс квантования, распространяя условия непрерывности волновой функции и ее первой производной (называемые также граничными условиями) ОТ —оо до +оо и, более того, требуя выполнения условий нормировки результатов.
Поскольку волновая функция должна быть нормирована, ее величина не должна расходиться при л; -> —«>. Таким образом В1 = 0. В дополнение к этому граничные условия при х = а/2 приводят к:
![]()
|
Вс = - гс е(-у+і*>°/2Л/ |
![]()
|
2і к |
![]() (1.35)
(1.35)
Величины Ас и Вс связаны следующим соотношением:
|
К - і ка к + і ка |
|
= е2 |
|
|
Cos2 |
|
(1.41) |
|
Имеется два типа решений, которые выражаются последующими трансцендентными уравнениями. |
|
(1) Четные решения |
|
К - ка к + ка |
|
(1.42) |
|
— _Єі ка |
|
Или |
|
Ка |
|
К * — = tan к |
|
Граничные условия при х = а/2 дают: Аге*а/2 + Вгека/2 = i4ceite/2 + Bce~ika/2 i k Лгека/2 - Д. е-™/2 = —(Aceika/2 - ^се-(^/2>) К Подстановка (1.37) в (1.35) дает: , [(/с + ik)2&ka - (к - iA:)2e-iAr" ] 4ifc/c D К2 + к2 . . Br =------------ sin fazA 2 Кк |
|
E-Kfli4/ |
 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
 |
|
Ка} ~2 |
|
К, (ка'I =сtan Ь |
|
>0 |
|
COS |
|
|
|
|||
|
|
||
|
|
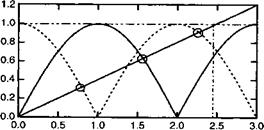
Ка/л Рис. 1.2. Графическое определение квантованных состояний для симметричной квантовой ямы шириной а = 10 нм (см. пример) с использованием уравнений (1.43) и (1.46) при к0 = 0,78 нм1. |
Где п обозначает л-ное решение уравнения. Величины Ап и Вп получаются, если обратить внимание на то, что интеграл от квадрата у/п(х) в интервале от —«> до +«> равен 1. Для основного состояния (п = 1) мы получаем:
|
Л = |
![]() 1/2
1/2
А + 2 / к
(1.446)
1/2
|
В, = |
![]()
|
£-ка / 2 |
![]() А + 2 / к
А + 2 / к
Где кх — волновой вектор основного состояния, определяемый (1.43). Уравнение
(1.44) показывает, что электронная волновая функция проникает в барьер на глубину, задаваемую величиной 1 /к. Это означает, что вероятность найти электрон в барьерной области отлична от нуля (см. рис. 1.1). Это явление, известное как туннелирование, не имеет классического эквивалента, в основе своей происходит из волновой природы электрона и напоминает аналогичное поведение света. Теперь вспомним уравнение, связывающее энергию собственного состояния и глубину проникновения в барьерную область:
|
1 |
![]()
|
П |
![]() (1.45)
(1.45)
(2) Нечетные решения
Этот случай соответствует альтернативному решению уравнения (1.39):
К - к
: ЄІЬ
К + ік
|
(1.46) |
![]() А именно:
А именно:
|
Ка |
![]() К (ка
К (ка
|
< 0 |
![]() -К- Чт
-К- Чт
В этом случае уравнение (1.36) говорит нам о том, что Ап = —Вп, т. е. решения являются нечетными. В этом случае энергетические уровни даются пересечением прямых линий с наклоном 1 /к0 и другой серии синусоидальных полуволн (сплошные линии на рис. 1.2).
Представляет интерес рассчитать число квантовых уровней в яме. Анализ рис. 1.2 дает:
N = 1 + Int f. (1.47)
/г п
Где символ Int означает «функцию целого числа».
К тому же, сколько бы мелкой ни была яма, в ней всегда имеется, по крайней мере, одно квантовое состояние. В то время как это замечание имеет общий характер и относится ко всем одномерным ямам, это может быть несправедливо в отношении трехмерных систем. Квантовые уровни называются также и локализованными,, поскольку волновые функции имеют непренебрежимую величину только в окрестности ямы; они называются также и связанными, так как вероятность найти электрон значительна только поблизости от ямы (электроны не являются подвижными и не могут участвовать в переносе тока). Энергетические уровни над барье
Ром (Е > 0) называются делокализованными или свободными (для получения дополнительной информации ознакомьтесь с дополнением 1.А).
Важно отметить, что приведенный ход рассуждений может быть обобщен на случай любого потенциала: т. е. квантование энергетических уровней следует из распространения граничных условий в интервале от — «> до +«>, а также из требования, чтобы амплитуды волновых функций исчезали на бесконечности.
Пример-----------------------------------------------------------------------------------------------------------------------------------------------------
Позже в главе 8 мы увидим, что электрон в полупроводниковой гетероструктуре, изготовленной на основе GaAs/Al0 45 Ga055 As, находится в условиях потенциальной ямы глубиной 360 мэВ. Более того, взаимодействие электрона с периодическим потенциалом кристаллической матрицы GaAs учитывается умножением массы электрона на коэффициент 0,067, при этом такое произведение соответствует эффективной массе электрона т' = 0,067 те. Использование уравнения (1.33) позволяет нам получить выражение для волнового вектора к0 в виде:
К0 = у1(2 х 0,067 X 0,9 х КГ’Чкг) х 0,36 (эВ)х 1,6 х 1019(Ал )/ 1,05 х 10'“(Дж с)
Или к0 = 0,78 нм-1, что соответствует длине волны 8,05 нм.
Теперь рассмотрим квантовую яму шириной 10 нм. Поскольку ширина ямы сравнима с длиной волны де Бройля /0, связанной с потенциалом К0 = 360 нм, мы можем ожидать, что система будет проявлять эффект квантования. Используя уравнение (1.47), мы видим, что в рассматриваемом случае мы можем ожидать присутствие трех связанных состояний в этой конкретной системе (т. е. 1 + Int(0,78 х 10/3,14)). Волновые функции, соответствующие каждому из этих состояний, показаны на рис. 1.1.
Приведенная ниже программа MATEMATICA очень полезна при решении задач на ограничивающие потенциалы.
M0=0.911СТ-30 (*kg*);hbar=1.051СГ-34 (*J. s*); q=1.610’-19(*C*);
Meff=0.067 (* effective electron mass in GaAs*);
V0=.36 (*well depth in eV*); a=10.(*well width in nm*);
KO=Sqrt[2*meff*mO*q*VO]* 10”-9/hbar (*in nm-1*)
Eq1=Cos[k*a/2];
Eq2=Sin[k*a/2];
Eq3=k/k0;
Plot1=Plot[Abs[eq1],{kAkO}] plot2=Plot[Abs[eq2],{klOlkO}] plot3=Plot[Abs[eq3], {k,0, kO} ]
Show[plot1 ,plot2,plot3] FindRoot[eq1==eq3,{kl0.2}]
E1 =hbar»2*(k*10* ’9)»2/(2*meff*m0*q)/.% FindRoot[eq2==eq3, {k,0.5}]
E2 =hbar»2*(k*10”9)”2/(2*meff*m0*q)/.% hnu=E2-E1 (^optical transition energy in eV)