Оптоэлектроника

Когерентное состояние

Глаубер был первым, кто представил физическое состояние, позволившее приме­рить волновой и корпускулярный подходы к фотонным состояниям. Мы не будем здесь детально обсуждать гипотезу Глаубера, хотя наше последующее объяснение может показаться отчасти произвольным. Рассмотрим резонатор, обладающий един­ственной одномерной модой с частотой со (обобщение на случай трех измерений и многомодовые возбуждения могут быть осуществлены сразу, но это влечет за собой определенные трудности с обозначениями). Состояние Глаубера или когерентное состояние определяется следующим соотношением:

а) = УЛи^)Щт) (2.57)

Т Л/А«!

Когерентное состояние Глаубера

Вероятностная интерпретация квантовой механики позволяет понять нам зна­чение этого состояния следующим образом: |«) есть состояние в резонаторе, для которого имеется вероятность:

Р = е-К И - (2.58)

Т

Нахождения т фотонов в резонаторе. В выражении (2.58) мы узнаем закон Пуассона теории вероятности. Этот классический закон дает вероятность нахождения т фо­тонов в резонаторе в процессе произвольной выборки при условии, что в среднем в резонаторе имеется а2 фотонов.

Ясно, что Ы) есть нормированное физическое состояние:

5>»=е+|1Х¥-=1 (2-59)

Т т

Попробуем оценить изменение такого состояния в течение времени. Предпо­ложим, что в момент времени / = 0 резонатор находится в состоянии, определяе­мом (2.57), т. е., что состояние (2.57) соответствует |а(0)). В соответствии с уравне­нием (1.29) глауберовское состояние |аг(/)> изменяется следующим образом:

|яг(/)) = е-Й1/2)-у—е-^«'/*!/!!) = е-(К/2)-у=е-1И™ + 1/2>|/и^ (2.60)

Т !П. т ш

Это выражение сразу принимает вид:

И)> = е-'*У е"[|И“)| /2] £с£» (2.61)

т

Поскольку каждое физическое предсказание относительно состояния | а(ф не­чувствительно к фазе е_1й", видно, что временная эволюция глауберовского состоя­ния |а(ф может быть представлена в виде:

(2.62)

Дадим теперь соотношение, образующее основу квантовых свойств глауберовс­кого состояния:

(2.63а)

Или в сопряженной форме:

(аа+ = а*(а

В самом деле:

Аа) = ^ ъАаг/2)-^=ат) = ^ е-(аР/2)-у= у[тт - 1) (2.64)

Т V т т V т!

В этой сумме мы перейдем от индекса суммирования т — 1 к п, так что:

Что мы и хотели показать.

С другой стороны, следует заметить, что а+а) не дает нам ничего полезного. Уравнение (2.63) позволит нам легко оценивать средние значения для наблюдае­мых. Сначала отыщем среднее число фотонов А^а в глауберовском состоянии |а):

А^а = (сф+я|а) = а* а = |а|2

Аналогично, средняя величина квадрата числа фотонов в этом состоянии есть:

Эти уравнения являются характеристиками распределения Пуассона и могли бы быть получены непосредственным использованием теории вероятности. К тому же мы видим, что среднее число фотонов и связанная с ним стандартная дисперсия не зависят от времени. И, наконец, это состояние подчиняется закону больших чисел, а именно:

(2.69)

Это последнее уравнение может быть записано также в виде: с / м _ (средняя величина У N1 _ - тт-

/ (___________ ~ л Т 2 ~ а

(дисперсия ) Д#02

Где 5/# обозначает отношение сигнал/шум, связанное с пуассоновскими флуктуа­циями числа фотонов. Это последнее соотношение образует основу теории детек­тирования, которая будет приведена в главе 11.

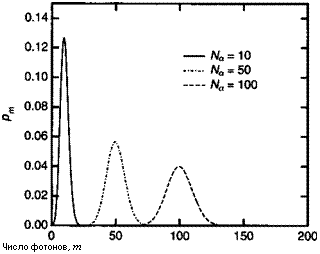
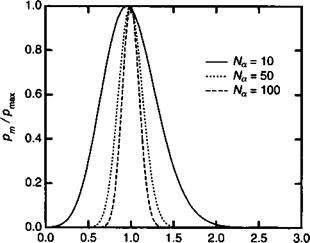
Рис. 2.1 иллюстрирует распределение Пуассона для трех значений среднего числа фотонов ЛГа. Отметим, что это распределение сужается по мере увеличения средне­го числа фотонов.

Теперь отыщем среднее значение наблюдаемой Е± а для электрического поля в глауберовском состоянии |а). В соответствии с уравнениями (2.34) и (2.35):

Е± а(а|Ё±|а) = іР(аа^їкг - а+е [кга)єп

Где поле вакуумных флуктуаций, определяемое (2.35), с учетом (2.63л) и (2.63б) имеет вид:

Ех, а = іГІря*г - а*с'Л'

Подобным же образом дисперсия наблюдаемой для электрического поля дается выражением:

|^Еj.)21or) = - F2(a |a2e2ik r + a+2e~2ikr - a+a - a+ae) (2.73)

Или:

A = F2[(areikr - a*e ikr)2 + 1] (2.74)

Вводя вновь соотношение (2.72), описывающее временную эволюцию, и пред­полагая также без потери общности, что а есть действительное число, равное а0, мы, в конце концов, получаем выражение для временной зависимости среднего электрического поля:

Е±,«(0= sin (к • г - сы)вп (2.75)

Что соответствует классическому электрическому полю:

® classical

(t) = Е0 sin( к г - cot)en (2.76)

Используя (2.35) и (2.66), получаем выражение, связывающее амплитуду клас­сического электрического поля Е0 электромагнитной волны с частотой со и средним числом фотонов N в резонаторе с энергией Ь со:

Е'-IW* <1771

Амплитуда электрического поля, выраженная через среднее число фотонов с энергией h со

Это последнее уравнение может быть интерпретировано с использованием корпускулярной модели. Среднее число фотонов N в резонаторе дается отноше­нием электромагнитной энергии, запасенной в резонаторе е0, VE2/2, и энергии,

Переносимой каждым фотоном Ь со. Мы также можем определить фотонный по­ток входящий или выходящий из резонатора за единицу времени, через единич­ную площадь, используя оптическую мощность, приходящуюся на единицу пло­щади Р:

Р = ПсоФ (2.78)

Пример-------------------------------------------------------------------------------------------------------------

Падающий поток «оранжевых» фотонов (h со =2 эВ) в пучке с плотностью энергии

1 мВт/см2 (Р= 10"3 Вт/см2) составляет:

Ф = 10"3 Вт/см2/(1,6 х 10"19 Кл х 2 эВ) = 3 х 1015 фотононов см'2 с-1

Плотность падающих «оранжевых» фотонов с энергией Ьа)—2 эВ, соответству­ющей напряженности электрического поля 1 В/см (Е0 = 100 В/м), составляет:

N/L =104 (В м"1)2 х 8,85 х 10"12 Ф"1 м/(2 х 1,6 х 10"19 Кл х 2 В) = 1,4 х 10п м"3

Таким образом, даже в случае очень умеренных уровней оптической мощности и напряженности электрического поля, огромное значение числа участвующих фо­тонов делает трудно наблюдаемой корпускулярную природу этих частиц. Тем не менее, вскоре мы столкнемся с приборами, способными детектировать одиночные фотоны. Поразительно, но человеческое зрение, при возможности адаптироваться к темноте в течение нескольких минут, способно обнаруживать фотонные потоки амплитудой в несколько фотонов в минуту.