Оптоэлектроника

Генерационно-рекомбинационный шум

Процесс электронно-дырочной генерации не создает абсолютно постоянный ток, т. к. электроны и дырки несут дискретные заряды, а момент их рождения является случайным. В этом случае флуктуации тока возникают из-за флуктуаций концент­рации свободных носителей в полупроводнике. Из (11.А. 17) мы видим, что для того, чтобы флуктуации концентрации генерировали флуктуации тока, средняя скорость носителей должна быть отличной от нуля. В противоположность теплово­му току генерационно-рекомбинационный шум присутствуют только в том случае, ког­да ток имеет ненулевое значение. Это, в свою очередь, требует того, чтобы в полу­проводнике были электрическое поле или градиент концентрации носителей.

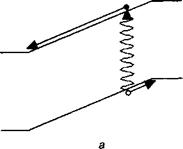
Проследим «судьбу» электрона, возникшего в момент времени ^ и путешеству­ющего со скоростью V, вплоть до его «трагического исчезновения» из зоны прово­димости вследствие рекомбинации в более поздний момент времени tk + тк (смот­рите рис. 11.А.4). Вклад этого события ‘к’ в ток цепи составляет /Д/ — tk), где:

0 < г < - г*

/. (11.А.30)

0, / < 0 или тк < /

Таким образом, полный ток составляет:

(11.А.31)

К

Мы можем записать средний ток в виде:

(1) = ~(т){й) <11А32)

Здесь N есть скорость генерации и (г) — среднее время жизни электрона. Такой процесс генерации может иметь разнообразную физическую природу: генерация на

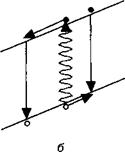
Рис. 11.А.4. Электрон, возникший в диоде, генерирует ток во время своего движения к /^-контакту; с дыркой происходит то же самое в л-контакте (а). В фото­проводнике возникший электрон рекомбинирует с дыркой в полупро­воднике (б).

Примесном центре (как это имеет место в случае механизма Шокли—Рида, иссле­дованного в разделе 6.5), эффект Оже (смотрите дополнение 6.Г), межзонная тер­моэлектрическая эмиссия (смотрите дополнение 10. Б) или поглощение фотона. Во всех этих случаях мы можем предполагать, что распределение времен возникнове­ния электронов следует распределению Пуассона, т. е., что отсутствует временная корреляция между событиями создания электронов.

В соответствии с нашей теперь уже хорошо отработанной процедурой спектр мощности генерированного тока есть:

■?/,(<») = J(/(?y(f+ r))e-i0"dr= (11.A.33)

Это выражение может быть рассчитано с использованием Фурье-образа для эле­ментарного вклада ik:

Ik(t-h)= f — h (©) eio'e-i«'.

{ 2n

(11. A. 34)

H (*>)= f h (Oe-'^'d/ = - —6 ■”

TOC o "1-5" h z Ј L io)

Это выражение, будучи вставлено в (11.30), дает:

Sn(p))= J dr J—L J eifi,2re-i(№r x /е*^>]Г ik(a)l )e-ifi,/* i,(a) 2)е^> =

2n 2n k i /

(11.A.35)

= ik(o)

2 П

В этом усреднении сумм мы имеем два различных случая:

• Поскольку времена создания и жизни электронов не являются коррелированны­ми при кф I каждая сумма принимает вид:

X '* ^ = % (0)) (11.А.36)

В интеграле (11.А.35) для Бп эти средние величины дают квадрат среднего тока.

» При к = /, когда среднее от двойной суммы в (11.А.35) может быть записано в виде:

+ -^ХКИ2) (11.А.37)

Это выражение приводит к простому результату для автокорреляционной функ­ции флуктуаций тока:

(х М*) -(? ■ (т)’(?'*’) ■ Нт )>>

(11.А.38)

Используя уравнение (11.А.32) для среднего тока, мы получаем следующий результат: При этом усиление g имеет вид: (11.А.39)

Здесь: усиление фотопроводимости было введено в разделе 11.3, а т1т есть время переноса электрона через генерационно-рекомбинационную область. В этом слу­чае мы получаем следующий общий результат для генерационно-рекомбинационно­го шума:

— (г[20])

/2 = 2^/ -t-Av (11. А. 40)

(г>

Г енерационно-реком - бинационный шум

Таким образом, как это и предсказывалось, этот вид шума присутствует только при событии, связанном с ненулевым средним током. В связи с этим выражением особый интерес представляют три случая:

1. Фотодиод без рекомбинации. В этом случае распределение времен жизни име­ет особенно простой вид. Создаваемый электрон будет иметь время жизни г1г, кото­рое позволит ему дойти до ^-контакта, где он мгновенно рекомбинирует. Таким образом, мы имеем # = 1 и (г2) = (г)[21] при отсутствии каких-либо флуктуаций по г. В этом случае рассматриваемый процесс представляет собой в чистом виде генера­ционный шум:

1;=2я1Ау (11.А.41)

Генерационный шум

Пример --------------------------------------------------------------------------------------------------------

Предполагая, что ток с амплитудой в 1 нА пересекает фотодиод, а ширина поло­сы составляет 1 кГц (11.А.41), мы приходим к генерационному шуму с амплиту­дой л/(2 х 1,6 х 10"19 С х 10~9 А х 10_3 Гц) или 0,56 пА.

Р(т)= у—ехр (т)

Среди прочего это соотношение обладает тем свойством, что (г2) = 2(г)2.Это приво­дит к генерационно-рекомбинациолнному шуму:

= 4да/Ду (11.А.43)

Г енерационно-реком - бинационный шум

Генерационно-рекомбинационный шум может рассматриваться как генераци­онный шум 2q(I/g)Av, усиленный с коэффициентом усиления g, к которому добав­ляется рекомбинационный шум. В фотодиоде рекомбинационный шум равен нулю: в то же время в фотопроводнике это шум того же типа, что и генерационный шум. Это, в свою очередь, приводит к удвоению генерационного шума и ответственно за появление коэффициента 4 в уравнении (11.А.43).

3. Шум генерации-захвата в квантово-размерных фотоприемниках. Как мы виде­ли, когда электрон пересекает квантово-размерную структуру, он может быть зах­вачен с вероятностью рс. Вероятность того, что электрон будет захвачен после того, как он пройдет п ям за пределами той ямы, из которой он был изначально фотовоз - бужден, составляет рс( — р)п~ при этом средние времена жизни составляют:

М = —. {*2) = [—(11. А. 44) х/ т ' ' I V, #

Здесь Ь^ есть расстояние между последовательными ямами. Шум, соответствую­щий (11.А.40), в этом случае составляет:

/г = 2(2 - рс )qgІAv (11.А.45)

Г енерационно-рекомбинационный шум в структуре с набором ям

При этом два предела имеют вид:

• рс -» 1 (фотодиодный предел, т. к. захват электрона близлежащей квантовой ямой неизбежен),

• рс -» 0 (фотопроводниковый предел, т. к. вероятность захвата является пуассонов - ским процессом, поскольку электрон пересечет много ям до того, как он будет захвачен).

Мы напоминаем, что g = 1/рсК где Доесть число квантовых ям.