Оптоэлектроника

Флуктуации

Рассмотрим ток /(*), циркулирующий по цепи. В реальной ситуации этот ток флук­туирует около среднего значения, соответствующего уровню сигнала. Наблюдате­лю, лишенному каких-либо средств обработки сигнала (например, интегрирования сигнала и т. п.), этот шум помешает зарегистрировать сигнал с уровнем, меньшим амплитуды хаотичных флукутаций. В связи с этим мы теперь разработаем физичес­кий и математический инструментарий, позволяющий нам количественно работать с этой простой, но фундаментальной шумовой моделью.

В рассматриваемом случае ток /(*) является примером случайного (стохастичес­кого) процесса. Случайный процесс есть функция, являющаяся следствием случай­ной выборки /(*, £), где ^есть случайная переменная (смотрите рис. 4.Г.2). Говоря более точно, такой процесс описывается набором функций /(/, £), —^ < <*>, связанных с распределением вероятности /(С), где/(^) — вероятность проявле­ния функции /(/, £). Как обычно, мы определяем среднее по ансамблю в виде (/(0) = 0/(0^ и (/2(0) = и2(и Для стационарных стохастических

Процессов, а лишь эти процессы мы и будем здесь рассматривать, это среднее не зависит от 1 Более того, мы дадим новое определение /(/), вычитая среднее значе­ние (/(*)) (которое фактически соответствует сигналу) из флуктуирующего тока так, что среднее значение (/(*)) будет равно нулю. Это делается из соображений удоб­ства, так как облегчает многие последующие выражения.

Хотя простые средние значения не зависят от времени, временные аспекты флуктуаций при этом не исчезают. Ток в момент времени tl может иметь различную величину в момент времени t. Этот эффект называется памятью стохастического процесса. Мера этой памяти может быть найдена с использованием автокорреляци­онной функции для /, которая является средним /(0*(^) по ансамблю:

^ ) = (К/Х/, )> = | К'; <Г >(/, ;<Г)/(<ГК

Идея, лежащая в основе (11.А.2) заключается в том, что, если процесс не обла­дает памятью, тогда /(*) и /(^) являются независимыми случайными переменными и среднее от произведения равно произведению средних, что превращает (11.А.2) в ноль. В случае стационарных процессов функция 5.. зависит только от разницы Т= tl — t. Более того, очевидно, что мы имеем 5..(т) =

Фурье-образ автокорреляционной функции называется спектром мощности /:

Спектр мощности /(О

Мы можем лучше понять причину того, почему мы называем это спектром мощности, рассчитав квадрат тока /(0 в течение большого временного интерва­ла Т. Ток, стробированный в интервале от — Т/2 до Г/2, мы можем разложить в ряд Фурье:

(11.А.4)

При этом мы получаем для квадрата тока:

Это выражение позволяет получить среднее по времени от квадрата рассматривае­мой величины:

(11.А.6)

Последнее соотношение есть ничто иное, как теорема Парсеваля. Подставляя вы­ражение для /(й^) в это последнее выражение, мы находим:

Л / * *■ / * '

— J/2(*)df = J/(f)e~/e*' d/ - — Jdre /ь*' — j*/(/)/(/ + r)dt (11.A.7)

T _т/2 к T _т/2 к T _T/2 T _T/2

Этот последний интеграл представляет среднее по времени от переменной i(t)i(t + т). Если среднее по ансамблю для этого интеграла в пределе Т -» «> равно автокорреляционной функции Sn(t)9 то в этом случае такой процесс называется эргодическим процессом. В дальнейшем мы будем предполагать, что механизмы фо­тодетектирования являются эргодическими процессами. Можно показать, что это свойство удовлетворяется, если интеграл от tSn(t) сходится.

Таким образом, следствие эргодичности для (11.А.7) заключается в следующем:

(11.A.8)

В пределе при T -> оо имеет место:

(11.А.9)

Здесь мы преобразовали сумму в интеграл, учитывая, что Аcok = In/T и используя соотношение:

(11.А. 10)

Уравнение (11.А.9) означает, что полное среднее ii) распределено по частотному спектру, определяемому ^(v), при этом, поскольку мы не делаем различия между положительными и отрицательными частотами (смотрите рис. 11.А.1), мощность по полосе положительных частот А уесть:

(11.А.11)

Средняя мощность в полосе частот А у

Для проведения расчетов нам необходимо извлечь из спектра мощности шума еще одно важное свойство. Рассмотрим передаточную функцию линейного фильтра И(со), которая преобразует сигнал 1п(со) в выходной сигнал /оШ(<у) = /г(со)1[п(а>). В соответ­ствии с теоремой свертки мы имеем:

(11. А. 12)

Теперь найдем функцию корреляции между /ош и /іп:

SJr) = (іоШ (/>',„ (t - г)) = J (t - t% (t - r))dҐ = J /г(/%(г - t')dt' = h{r)*S„(t)

(11.А. 13)

Автокорреляционная функция для /ош определяется умножением (11.А.12) на /out(f + *):

$Л) = {'оиХ( + тУЛ} = [ Ь({'Х’°Л* + *)«(* - ''Ж = f А(?'К(г + Ф’ = А(- 4SoX~ *)

J J (11.A. 14)

Или вновь:

S„ (О = h(- ?)*К*)*$Л*) (11.А.15)

Это выражение позволяет получить Фурье-образ в виде:

S„(fi>)= |А(«)| 2Su((o) (11.А.16)

Преобразование спектра мощности фильтром

Этот важный результат позволяет восстановить (11.А.11) на фоне средней мощнос­ти шума, поскольку фильтр (h{cd) = 1, если о)у< со < со{ + А со и h(aj) = 0 при других частотах) передает мощность S(co)дct). В дополнение к этому это уравнение показы­вает, что расчет распространения шума в линейной цепи полностью аналогичен распространению обычного сигнала, если мы представим шум в виде амплитудного источника iv, квадрат амплитуды которого дается (11.А.11). Вооружившись этими общими результатами, мы можем теперь обратиться к проблеме идентификации физической природы шума приемника излучения.

Пример--------------------------------------------------------------------------------------------------------------

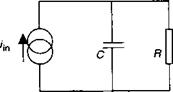
Для простой интегрирующей цепи на рис. 11.А.2 мы легко находим:

H{(o)= = —------- , г = RC

Ija)) 1 + i ®г’

В этом случае показано, что, если спектр шумового источника на входе есть Su(co)9 то спектр мощности на выходе есть:

1

■$,»=

Рис. 11.А.2. Интегрирующая цепь.

Таким образом, фильтр значительно ослабляет шум за счет устранения части спектра мощности выше со = 1/г. Чем больше величина г, тем больше и величина фильтрации.