Двумерные экситоны
Мы видели, что в квантовой яме движение электронов может быть ограничено в пределах области размером в несколько нанометров, т. е. на расстоянии, значительно меньшем боровского радиуса трехмерного экситона. Следствием этого ограничения является то, что зоны квантуются в виде подзон, разделенных интервалом в несколько десятков мэВ, что превышает энергию связи трехмерного экситона. Применительно к корреляции между электронами в основной зоне проводимости и дырками в основной валентной зоне кулоновское взаимодействие может иметь место только в направлении, параллельном границам раздела. По сравнению с потенциалом ограничения кулоновский потенциал не играет существенной роли в перпендикулярном направлении. В этом случае экситонная волновая функция представляет собой:
У(г„ г2) = -±-£с(К„ К2)С(г,)е'к'к'«с0(г1К1"(г2)е'к>к-'«„()(г2) (8.Б.14)
К».к.
Здесь векторы И и К обозначают движение, параллельное границам раздела. Используя те же самые преобразования, что и в предыдущем разделе, получаем уравнение Шредингера, управляющее движением частиц в плоскости:
|
2 . |
![]() 2 2
2 2
Г Ь К с »• „
|
*(К) (8.Б.15) |
![]() Е-^м-с' -£' - Е■
Е-^м-с' -£' - Е■
2т1
При этом эффективный потенциал взаимодействия есть:
/ич (а а е С' М £ е /о с
Г-г(К) = «М*, ■ I,----------- =г ------------------------------ (8.Б. 16)
^ 4яед/Л + [г, - г2] 4жеЛ
Эта последняя аппроксимация действительна в предельном случае, когда огибающие функции характеризуются пренебрежимо малой протяженностью по сравнению с экситонным радиусом. Решение этого уравнения для «двумерного водородного атома» дает следующие собственные энергии:
В этом выражении используется та же самая эффективная константа Ридберга, которая была определена в последнем разделе.
|
Поглощение
|
|
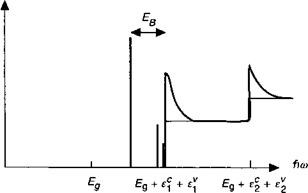
Энергия фотона (эВ) Рис. 8.Б. З. Спектр поглощения квантовой ямы, модифицированного корреляцией электронов и дырок, т. е. присутствием экситонов. По сравнению с процессом, в котором участвуют лишь свободные электронно-дырочные пары (тонкие линии), экситоны приводят к возникновению дискретных линий ниже края эффективной ширины запрещенной зоны, при этом каждая ступенька, обусловленная поглощением континуума, деформируется узким экситонным пиком (а). Этот результат выглядит особенно выразительно в экспериментах по квантовым ямам различной толщины (б) (по данным D. S. Chemla, and D. A. В. Miller, Adv. Phys. 38,89 (1989), перепечатано с разрешения Taylor & Francis Ltd. Http: Www. co. uk/joumals). |
|
|
Таким образом, двумерный экситон обладает энергией связи, в четыре раза большей по сравнению с эквивалентным трехмерным экситоном.
Пример
Рассмотрим квантовую яму GaAs шириной 5 нм. В предыдущем примере мы видели, что энергия связи трехмерных экситонов в GaAs составляет 5,6 мэВ. В этом примере ширина ямы намного меньше боровского радиуса экситона а* = 10,6 нм, при этом энергия связи составляет 4 х Ев или 22,4 мэВ. В результате этого существенная доля ансамбля экситонов (58%) останется в связанном состоянии при комнатной температуре. Соответственно в этом случае экситонные особенности в явном виде проявляются в полощении и люминесценции этих квантовых ям (смотрите рис. 8.Б. З).
В более реалистичном случае, когда пространственной протяженностью волновых функций g(z) и g(z) по сравнению с а*в полностью пренебречь нельзя, эффективное взаимодействие ослабляется по сравнению с чисто двумерным случаем, при этом энергия связи экситонов плавно уменьшается в направлении энергии связи трехмерных экситонов. Количественная трактовка этого эффекта требует, чтобы, помимо основных зон учитывались бы также и другие подзоны. Разумное описание этого промежуточного режима возможно только с использованием численных методов.
Как и в трехмерном случае, корреляция между электроном и дыркой кардинально модифицирует спектр поглощения квантовых ям. В области ниже края эффективной запрещенной зоны Eg + £,с + Ј, v спектр содержит дискретные линии. В области выше края зоны наблюдается увеличение поглощения по сравнению со случаем свободных электронов и дырок. Рисунок 8.Б. З качественно иллюстрирует модификацию спектров поглощения.