Дипольные моменты в прямозонных полупроводниках
Рассмотрим объем V кристаллического полупроводника, в котором собственные функции [¥п]) с энергиями даются функциями Блоха—Фуке, введенными в (5.12):
|
|
(7.1)
Напоминаем, что к есть волновой вектор собственного состояния, принадлежащего первой зоне Бриллюэна полупроводника и обозначающий положение состояния в л-ной энергетической зоне в направлении ек = к/к (смотрите рис. 5.2 и 5.4). Функции ип к(г) обладают периодичностью кристаллической решетки (т. е. для каждого вектора решетки г.: ип к(г + г.) = ип.(г)). Более того, эти функции нормированы на объем элементарной ячейки К, т. е. Iщ |нлк(г)|2сРг = К. Как уже объяснялось в дополнении 1.А, мы нормируем стационарные функции по отношению к виртуальному ящику объема У= А^К, при этом =1, что приводит к квазиквантованию волновых векторов
К. Напоминаем, что наиболее общепринятая процедура, используемая при квазикван - товании в кристаллических твердых телах, состоит в использовании циклических граничных условий Борна—фон Кармана, приведенных в (5.10). Наконец, важным моментом, достойным упоминания (а также полезным во многих случаях), является то, что пространственная вариация волновых функций е_1кг очень слаба по сравнению с той, которая возникает из-за атомных волновых функций ип к(г) (смотрите рис. 5.3). Другими словами, е-1кг действует как огибающая для блоховских функций.
|
(7.2) |
![]() На полупроводник действует электромагнитная волна, для которой гамильтониан возмущения для взаимодействия (смотрите (3.13)) может быть записан в виде:
На полупроводник действует электромагнитная волна, для которой гамильтониан возмущения для взаимодействия (смотрите (3.13)) может быть записан в виде:
Щт, г )= И/С05(к р • Г ~ ('){) — — <-/Е • Г СО$(кор ■ Г.............................. 0)1)
где г — оператор положения, кор — волновой вектор излучения, а Е — напряженность электрического поля. В этом случае гамильтониан оптического взаимодействия будет связывать два состояния |Тя к) и к,). Уравнения (1.82) и (1.83) позволяют рассчитать скорость вероятности (с-1) того, что электрон с волновым вектором к из зоны п попадет в состояние к' зоны п':
КК k)|2^(Д« = - ЕпЛ) (7.3)
Напоминаем, что векторы к квазиквантованы. Энергетическая зависимость дельтафункции Дирака выражает требование сохранения энергии:
Hco=E^-Enk (7.4)
Теперь рассчитаем матричный элемент Wn k я, ^
K. t.s. r = k'I»"Ik) = -^7-• JJJ«*-.k'(r>eik'r(r>e'ik” 4,k(T)e-‘krd3T (7.5)
Lattice
Этот последний интеграл может быть упрощен, если заметить, что функция ei(k,~ “k) г изменяется очень медленно по сравнению с произведением двух функций ип k(r). Таким образом, мы можем переписать интеграл в (7.5) следующим образом:
TOC o "1-5" h z
|
W Rv П, к, ri. |
![]() „'Ж = - у - ■ Xe'(k к> /// M*,k (r)rM„,k(r)d3r (7.6)
„'Ж = - у - ■ Xe'(k к> /// M*,k (r)rM„,k(r)d3r (7.6)
• Cell i
А интефал I в (7.6) может быть записан в виде:
I = JJj «*,k(R)(R + ri)M„,k(R)d5R =JJJ «;.k.(R)Ri»1Iik(R)d3R (7.7)
Cell / CeU О
Где R перекрывает пространство элементарной ячейки в области около 0. Член с г. в интеграле может быть устранен из (7.7), поскольку блоховские функции ортонормиро - ваны для к ф к'. В результате этого этот интефал не зависит от /-той ячейки, в пределах которой производится его оценка. В этом случае уравнение (7.6) приобретает вид:
= =-|р-Щк'-кор-к) (7.8)
Где функция Кронеккера в последнем члене выражает требование сохранения момента при электрон-фотонном взаимодействии:
К' = к7 + кор (7.9 а)
Сохранение момента при оптических переходах
Волновые векторы фотонов в видимом и близким к видимому спектральных диапазонах сильно отличаются друг от друга: кор = 2я/Я ~ 104 — 106 см-1, тогда как типичные волновые векторы в зоне Бриллюэна по порядку величины составляют к = Inja или 108 см-1 (напоминаем, что а есть постоянная решетки). Таким образом волновой вектор излучения является пренебрежимо малым по сравнению с этим же параметром для электронов в каждой из различных энергетических зон, так что:
К'«к (7.96)
Оптические переходы являются «вертикальными»
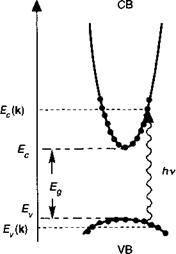
Рисунок 7.1 иллюстрирует тот факт, что оптические переходы в зонной диаграмме должны иметь место при постоянной величине к. Именно в этом смысле такие переходы называют вертикальными. Очевидно, что это правило для переходов может быть реализовано, если зонная структура имеет прямой характер, т. е. если экстремумы валентной зоны и зоны проводимости выровнены по вертикали в зоне
|
ИсМ <г> е |
![]()
|
1к г |
![]()
|
-1к г |
![]() Рис. 7.1. Оптические переходы между состояниями зоны проводимости и валентной зоны имеют место при постоянной величине к. Такие переходы называют «вертикальными».
Рис. 7.1. Оптические переходы между состояниями зоны проводимости и валентной зоны имеют место при постоянной величине к. Такие переходы называют «вертикальными».
------------------------------ ► к
Бриллюэна. Ситуация с переходами в непрямой зонной структуре более сложна и не рассматривается в этой книге. Таким образом, в будущем мы сможем устранить индекс к' из (7.8).
Начиная с этого момента и далее мы ограничимся оптическими переходами между валентной зоной и зоной проводимости. Будем обозначать через иА и ил периодические компоненты блоховских функций соответственно в зоне проводимости и валентной зоне. В этом случае дипольный матричный элемент И^(к) для переходов между валентной зоной и зоной проводимости принимает вид:
Ж (к) = -<?Е • г £(к' - к - к)
Ж ор (7.10)
= //1М*к(К)КИ‘,'к(К)д3К
Дипольный матричный элемент для переходов валентная зона -» зона проводимости
Теперь мы можем использовать (3.9.6) для того, чтобы связать матричные элементы операторов оптического взаимодействия А • р и Б • Е:
/
Г =------------- р
Тпо),
(7.11а)
Г*0 ма1^а с;льмрипа а вакууме, а п вСТЬ ЭНерГвТИЧвСКИЙ ЗаЗОр МеЖДУ ДВуМЯ
Состояниями в зоне проводимости и валентной зоне. Мы видели в дополнении 5.В, что может быть получен исходя из параметра Кейна Р. Эта формула чрезвычайно полезна, так как величина Р практически постоянна в соединениях III—V (смотрите таблицу 7.1), что делает (7.10) достаточно предсказуемым. Более того, используя теорию Кейна, мы можем легко показать, что в первом порядке по к, матричные элементы (7.11а) являются постоянными. Уравнение, связывающее рус с параметром Кейна Р, может быть найдено в литературе в таком количестве различных форм, сколь велико и число определений этого параметра. В (5.В.18) мы использовали предположение, что <г*Р2 является параметром, гомогенным по энергии». Другие авторы используют предположение, что «Р есть параметр, гомогенный по скорости, а
третьи, предполагают, что этот параметр гомогенен по импульсу».Б нашем рассуждении мы предпочитаем использовать энергию Кейна Ер (= Р2), что является единогласно признаваемым параметром (20—25 эВ) и это приводит к следующему результату:
![]() (7.116)
(7.116)
Дипольный матричный элемент и энергия Кейна
Где Е есть ширина запрещенной зоны. Также популярным в литературе параметром является матричный элемент хус. Это понятие вводится с тем, чтобы учесть тот факт, что в оптических переходах принимают участие только подзоны легких и тяжелых дырок, а не спин-орбитально отщепленная подзона, которая отстоит достаточно далеко по энергии. Мы могли бы использовать элементы перехода, введенные в (5.В.22), но идея, лежащая в основе этих расчетов, достаточно проста: только две трети силы осциллятора (т. е. две зоны из трех) принимают участие в переходе, что приводит к:
2
|
(7. Не) |
![]()
|
Тп |
![]() _ h2 Х"с 3 Е]
_ h2 Х"с 3 Е]
В таблице 7.1 приведены соответствующие параметры Eg, Е^ тJmQ, rw для основных полупроводников, используемых в оптоэлектронных применениях. Отметим, что в случае узкозонных полупроводников дипольный матричный элемент становится очень большим в сравнении с межатомным расстоянием, а электронные волновые функции становятся все более делокализованными по мере того, как уменьшается ширина запрещенной зоны. В этом смысле принято говорить о том, что полупроводники становятся все более квантовыми по мере уменьшения ширины их запрещенной зоны.
|
Табл. 7.1. Величина Е (ширины запрещенной зоны), тс/т0 (эффективной массы электронов), энергии Кейна Р и дипольного матричного элемента оптического перехода для различных полупроводников (из книги: G. Bastard, Wave Mechanics Applied to Semiconductor Heterostructures, Wiley, New York (1991))
|
Пример---------------------------------------------------------------------------------------------------------------------------------------------------
Энергия Кейна Ер в СаАз составляет 22,7 эВ и соответствует кейновской скорости:
|
= 1,42x10* м/с |
|
.6x10-” Кл |
![]() ГЁ7 _ /22,7 В х 1,1 :'2гц, V 2x0,9>
ГЁ7 _ /22,7 В х 1,1 :'2гц, V 2x0,9>
1x10'” кг
Матричный элемент /удается (7.116) и равен:
Гж = 1,05 х 10-34 Дж с х 1,42 х 106 м с~1/(1,5 В х 1,6 х Ю"19 Кл) = 6,14 А. Элемент х входит в расчеты поглощения и равен г х ^(2/3) или 5,0 А.