Оптоэлектроника

Динамическая интерпретация Эффективной массы и концепции дырок

Вплоть до настоящего момента мы несколько раз упоминали понятие дырка. В действительности, это сложное понятие, требующее (при последовательном рас­смотрении) привлечения теории многих тел. В этом разделе мы ограничимся лишь тем, что представим несколько интуитивных аспектов, касающихся теории дырок. Начнем с того, что представим динамическую интерпретацию концепции эффек­тивной массы.

Волновые функции электронов могут быть представлены в виде комбинации бегущих волн:

ВД = JJJe(k)e'(k,-^i')d, k

Или вновь, используя результаты раздела 5.2:

ЧЧГ>= I fff(к)и„,к(r)ei(ltd3к

Bands т

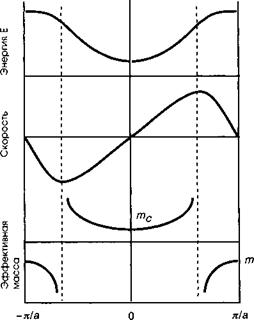
Волновые пакеты, сконструированные из волновых функций вблизи конкретной ве­личины к обладают групповой скоростью, определяемой дисперсионным соотношением vg = d(o/dk, так что в случае волн электронной материи в зоне (см. рис. 5.10) можем записать:

V =-V„Ј

Работа, совершаемая внешней силой Р в течение временного интервала d^ равна:

(5.27)

ЙЕ = —¥&

8

При этом изменение энергии волнового пакета сопровождается также сдвигом сред­него положения волнового пакета в зонной структуре и определяется соотношением:

DE = V. Edk = ~h v dk “ 8

(5.28)

Рассмотрение показывает, что центр волнового пакета, подверженного воздей­ствию силы Р, подчиняется таким образом соотношению:

Dk

Рис. 5.10. Связь между зонной струк­турой, групповой скоростью и эффек­тивной массой.

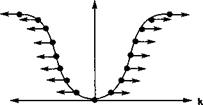
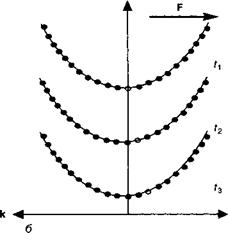
Отметим, что, если никакой механизм диссипиации энергии не противодействует воздействию этой силы Р, волновой пакет бу­дет двигаться или циркулировать по зонной структуре (см. рис.

5.11). Колебания, возникающие при циклическом обращении но­сителей по редуцированной зоне Бриллюэна, называются блоков­скими осцилляциями.

Пример -------------------------------

Время релаксации г между пос­ледовательными столкновениями в твердых телах составляет вели­чину порядка 0,1 пс. Предпола­гая, что напряженность электри­ческого поля Е составляет при­близительно 104 В см-1, находим,

Что волновой пакет получит смещение на йк « 106 см-1. Эта величина на­

Много меньше типичного размера зоны Бриллюэна (к/а » Ю8 см-1). Как следствие этого, блоховские осцилляции до сих пор не наблюдались в объемных материалах.

В том случае, когда диссипативные процессы полностью отсутствуют, элект­рон, подверженный воздействию однородной силы Р, будет однородно двигаться в к-пространстве и испытает соответствующее ускорение в реальном пространстве. Это ускорение определяется соотношением:

1 а Ч„Е = ич^кЕ]^- (5.30)

Й а/

П dt

Или, учитывая (5.29):

SHAPE \* MERGEFORMAT

А/ Й2

Матрица [УкУк£] не представляет из себя ничего другого как Ь2М~ где Месть матрица эффективной массы в (5.14). Та­ким образом, реакция волнового пакета может быть описана ньютоновской дина­микой с заменой массы частицы на ее эффективную массу /яеГ

Под влиянием электрического поля Е каждый элемент сРк зонной структуры дает

Рис. 5.11. В отсутствие столкновений электро­ны под воздействием электрического поля бу­дут циклично обращаться по зоне Бриллюэна периодическим образом. Это приводит к явле­нию, известному как блоховские осцилляции.

Вклад в элементарный объем сРк/8;г3, движущийся со скоростью у^(к) Таким обра­зом, электрический ток, проходящий через среду, составляет:

J = -*(*,) = -2* ///

Bnllouin zone

Или:

(5.33)

J (заполненная зона) = О

Материал, в котором последняя зона полностью заполнена электронами и от­делена запрещенной зоной от соседней близлежащей пустой зоны, не может про­водить электрический ток и называется изолятором. Если эта зона, которую мы обычно называем зоной проводимости, частично заполнена (вплоть до максимальной энергии = Етйх), электроны смогут приобрести скорость в к-пространстве, определяемую (5.31), и двигаться в направлении силы. Ток, возникающий из-за этих электронов не компенсируется из-за отсутствия сим­метрии (рис. 5.12). Такие электроны проводимости могут быть обеспечены как са­мим материалом (как это имеет место в случае металлов), так и быть добавлены в изолятор (как этот имеет место в случае полупроводников). Говоря конкретнее, в том случае, когда электрическое поле приложено вдоль оси Ох, электроны пере­носятся из состояний с кх < 0 в область с состояниями кх > 0, при этом через кристалл потечет ток, определяемый в момент времени t =0 (см. (5.32)):

(5.34)

Ал H

Этот ток будет монотонно возрастать со временем, поскольку Етах будет посте­пенно смещаться в направлении электрического поля. Понятно, что в течение пе-

J = 0

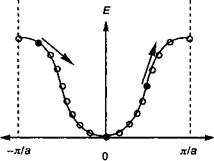
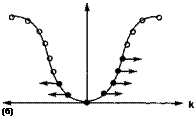
Рис. 5.12. В полностью заполненной зоне электрические токи, возникающие с участи­ем заполненных состояний при к и —к будут компенсироваться (а). В час­тично незаполненной зоне (б) электроны под воздействием силы Р, опреде­ляемой (5.26—5.29), приобретают скорость у. Таким образом, электроны пе­реносятся вдоль оси симметрии, при этом полный баланс скоростей является ненулевым. Таким образом, такая неполная зона может быть проводящей.

Реходного периода, длящегося несколько десятков пикосекунд, столкновения при­ведут к стабилизации тока. В стационарных условиях этот процесс описывается уравнениями Больцмана, которые мы рассмотрим позже в главе 6.

Аналогичным образом, если нам каким-либо образом освободить электроны из заполненной зоны (валентной зоны) и придать им энергию £т. п, возникающий при этом ток составит:

Dk„ x

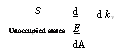(5.35)

Или с учетом (5.33):

(5.36)

Где пределы интефирования изменяются от Ет. п до вершины валентной зоны (рис. 5.13). Таким образом, мы видим, что ток, переносимый практически заполненной зоной, может быть интерпретирован как поток положительно заряженных квазича­стиц, таких как дырки. Рассмотрение, аналогичное проведенному ранее, показывает, что масса этих частиц положительна и определяется соотношением:

(5.37)

Поскольку кривизна вблизи максимума валентной зоны отрицательна. Рис. 5.13я показывает нам, каким образом «дырку» (т. е. незанятое электронное состояние в валентной зоне) можно рассматривать как несущую положительный заряд.

Читателю, впервые сталкивающемуся с такой концепцией может помочь аналогия с простой гидродинамикой. В этом случае электроны можно рассматривать как будто «падающими» на дно зоны проводимости подобно воде, стремящейся к дну стакана, в то время как дырки «поднимаются» к вершине валентной зоны подобно пузырькам (дыркам в жидкости) в стакане с шампанским.

Для завершения этого раздела нам остается добавить, что полная волновая функция дырки определяется переплетением собственных состояний всей валентной зоны (сим - метризованных в виде детерминанта Слэтера), из которых был удален один электрон. Этот тип функций является не очень востребованным на практике, но иногда используется, как, например, в теории экситонов.