Оптоэлектроника

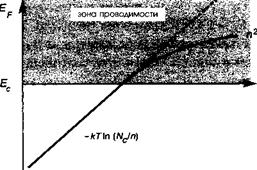
Энергия электронов Статистика носителей заряда в полупроводниках. Статистика Ферми и уровень Ферми

Электроны и дырки в полупроводниках подчиняются, как и все частицы со спином 1/2, статистике Ферми—Дирака. Таким образом, вероятность того, что при температуре Тсо­стояние с энергией Е будет занято, дается функцией распределения Ферми—Дирака /(£). При температуре Т функция распределения по энергии имеет вид:

(5.38)

Так, что концентрация носителей, например, в зоне проводимости полупроводника определяется соотношением:

П = ]рс (Е)ДЕ)1Е

Безусловно, ниже Ес не имеется разрешенных состояний. С учетом выражения для плотности состояний в зоне проводимости (смотрите (5.20)) это последнее урав­нение может быть записано в общем виде:

^сГ/2

Где Е1/2 есть интеграл Ферми и Ыс — эффективная плотность состояний в зоне проводимости.

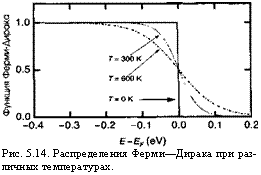
Рис. 5.14 иллюстрирует распреде­ления Ферми—Дирака при нулевой и ненулевой температурах. Мы долж­ны напомнить, что при температуре Т= О К энергия Ферми есть энергия последнего занятого состояния. По определению, уровень Ферми есть хи­мический потенциал частиц в систе­ме. Он описывает количество энер­гии, которое должно быть потрачено для того, чтобы добавить одну части­цу (расположенную изначально дале­ко) в систему. При термодинамичес­ком равновесии этот химический по­тенциал одинаков для всех частиц и идентичен по всей структуре. К этому очень важному моменту мы возвратимся позже во время нашего изучения диффузии.

При расчете положения уровня Ферми в полупроводнике в функции числа элек­тронов возникают две различные ситуации в зависимости от того, расположен ли уровень Ферми в запрещенной зоне или зоне разрешенных состояний зонной струк­туры материала.

Занятый уровень Ферми: вырожденная система (рис. 5.15)

В этом случае функция Ферми—Дирака может быть аппроксимирована ступен­чатой функцией:

/(£) = 1, если Е < ЕР

/(£) = 0, если Е> ЕР

В этом случае объемная плотность электронов дается перекрытием функцией Ферми и энергетической плотностью состояний на единицу объема в зоне прово­димости, т. е.:

(5.40)

Или иначе:

(5.41)

Отметим, что в этом выражении число носителей не является функцией температуры. Этот момент ха­рактерен для вырожденных систем таких, например, как металлы или сильно легированные полупроводники.

Пример------------------------------------------------------------------------------------------

Попробуем найти число носителей, соответствующих положению уровня Ферми, отстоящему на 30 мэВ вглубь зоны проводимости СаАБ. Для ваАз тс = 0,067/яе:

П = (2 х 0,067 х 0,91 х 10-30 кг/1,1 х 10“68 Дж2 с2)1’5 х х (0,03 эВ х 1,6 х 10-19 Кл^/Зп2

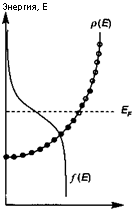
Рис. 5.15. Способ расчета положения уровня Ферми, когда он расположен в зоне разрешенных состояний.

Или:

П = 4,4 х 1017 см 3

Таким образом, при концентрации электронов выше 1017 см-3 GaAs ведет себя как металл и его уровень Ферми заполнен даже при температуре абсолютного нуля.

Незанятый уровень Ферми (рис. 5.16)

В этом случае уровень Ферми располагается в запрещенной зоне полупроводника. Число электронов вновь дается перекрытием функций распределения Ферми—Дирака для элек - троновД^Е) = 1/(1 — exp ((Е— Е^/кТ) и плотности состояний в зоне проводимости. В этом случае требуется другая аппроксимация для функции Ферми. Сейчас мы предположим, что уровень Ферми располагается достаточно глубоко в запрещенной зоне по сравнению с кТ, так что Е— ЕР » кТ. В этом случае функция Ферми — Дирака может быть аппрокси­мирована распределением Больцмана е -(Е-£г)/кТ (неквантовый режим):

Т. е.:

(5.426)

Концентрация электронов и уровень Ферми

Где, как мы напоминаем, т * есть эффективная масса для плотности состояний в зоне проводимости, определяемой (5.22). Ис есть эффективная плотность состоя­ний в зоне проводимости:

(5.43)

В том, что касается дырок, вероятность заполненияЕ) дыркой равна вероятности того, что это состояние не занято электроном. Это приводит к:

J + Q(E-EF)/kT ] + Q-{E-EF)/kT

Статистика Ферми—Дирака для дырок

ЦЕ) =1-/с(Р

Е

V

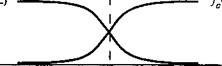
Рис. 5.16. Способ расчета концентрации носителей в полупроводниковых зонах в фун-

Кции положения уровня Ферми.

Таким образом, в больцмановском режиме концентрация дырок в валентной зоне связана с уровнем Ферми соотношением:

Р = | р(ЕУ(-Е-Е')/кТйЕ = Му^>-Е-)/кт

(5.45а)

Концентрация дырок и уровень Ферми

Где N — эффективная плотность состояний в валентной зоне, определяемая соот­ношением:

3/2

2т*кТ

Яй2

Термин «эффективная плотность состояний» приобретает свой смысл при учете уравнений (5.42) и (5.45). Статистика заселенности в полупроводниках имеет тот же характер, что статистика двухуровневой системы с энергиями Еу и Ес при энергетичес­ком зазоре Ес — Еу = Е8, определяемом запрещенной зоной, и плотностями состояний, определяемыми Иу и ТУ соответственно (смотрите рис. 5.18). Вводя значения соответ­ствующих физических констант, указанные эффективные плотности принимают вид:

(5.46)

Эффективные плотности состояний в полупроводниках

Пример---------------------------------------------------------------------------------------------------------

В случае ваАБ при 300 К т*с = 0,067 и т' = 0,64, что приводит к:

ТУ = 4,3 х 1017 см"3

С р

А^=1,3х1019см-3

При условии, что концентрации электронов и дырок известны, лля расчета положе­ния уровня Ферми полезны также уравнения (5.42) и (5.44):

N..

КТп^= Е„ + кТ1п-

(5.47)

Уровень Ферми и концентрация носителей

Таким образом, мы видим, что уровень Ферми проникает в зоны, т. е. полупро­водник становится вырожденным, как только концентрация электронов (или ды­рок) превысит эффективную плотность состояний (смотрите рис. 5.17).

Уравнение (5.47) интересно тем, что оно показывает, что уровень Ферми не представляет собой ничто другое, как изменение переменных без непосредственно физически добавленной величины. Это всего лишь мера плотности заселенности на энергетической шкале. В то же время эта концепция проявит всю свою силу в гетерогенных системах, являющихся основой физики приборов. В самом деле, по­стоянство уровня Ферми во всех областях, где превалирует термодинамическое равновесие, является одним из основных инструментов физики приборов.

И, наконец, если мы предположим, что электроны и дырки находятся в термо­динамическом равновесии, то они обладают также одним и тем же химическим

Потенциалом (т. е. химический потенциал имеет одно и то же значение там, где выполняются условия термодинамического равновесия). В большей степени мощь этой концепции мы оценим при исследовании аспектов физики приборов в главе 10. В соответствии с уравнениями (5.42) и (5.44) как их следствие мы находим, что произведение пр не зависит от положения уровня Ферми и составляет:

Пр = ЫсЫ^-Е’,кТ (5.48)

Закон действующих масс для полупроводников

Где £ = Ес~ Еу есть ширина запрещенной зоны. Выражение (5.48) устанавливает связь между концентрациями электронов и дырок в равновесных условиях и изве­стно, как закон действующих масс.