Диапазон вблизи края запрещенной зоны
В оптических свойствах материалов в рассматриваемом диапазоне доминирует процессы, связанные с полосой поглощения полупроводников. Простейшим подходом, учитывающим этот процесс, является модель Вепля и Дидоменико. Этот подход заключается в рассмотрении переходов между валентной зоной и зоной проводимости в виде единого ос - цилляторного перехода с резонансной частотой уо и силой осциллятора пЕа/2 (по историческим причинам Еа называется энергией дисперсии). В этом случае уравнение Зеллмайера может быть записано в виде:
< = 1 + Е”Е' (7.Б. З)
Это соотношение выполняется удивительно хорошо для целого ряда полупроводников и изоляторов. Тем не менее согласие между теорией и экспериментом оказывается недостаточным для оптоэлектронных применений, в которых принципиальную важность имеет прецизионный контроль оптических параметров. В связи с этим мы обратимся вновь к более феноменологическому подходу.
Для этого мы вспомним, что действительная ех и мнимая е2 части диэлектрической постоянной связаны соотношением Крамерса—Кронига:
Е{(Е)= 1 + |ру| ^[Ее АЕ' (7.Б.4)
0
Где РУ обозначает «главное значение». Отметим, что интеграл в (7.Б.4) показывает, что хотя поглощение и вводит в действие диапазон энергий, связанных с энергией
Фотона, на действительную часть диэлектрической постоянной влияет вся зонная
Структура, что делает расчет более сложным. Уравнение (7.Б.4) может быть представлено в виде ограниченного ряда:
Или в другом виде:
Е,(Е)= 1 + Л/, +М_}Е2 +М_5Е* +... (7.Б.6а)
Где моменты М. даются формулой:
М,,=- е,(ЕУЕ^Е (7.Б.66)
*{ '
Таким образом, мы ищем выражение для е2(Е), которое представляет собой просто поглощение в материале. Существуют различные модели, которые страдают определенной степенью произвольности, так как они включают в себя феноменологические коррекции кривой поглощения в полупроводниках (как правило, достаточно сложные). Здесь же мы ограничимся моделью Лфромовича, так как она является одной из наиболее пригодных для прикладных целей.
Эта модель использует аппроксимацию е2(Е) в виде функции:
Е2Е) = ^Е^Е^<Е < Е> (7.Б.7)
[О, в других случаях
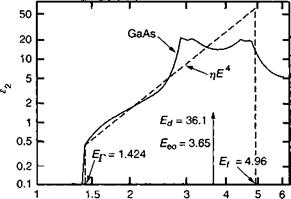
Вскоре мы увидим, как параметры модели связаны с Есо и Ел. Рис. 7. Б.2 демонстрируют, насколько хорошо эта формула описывает СаМ.
Это последнее уравнение показывает, каким образом можно рассчитать моменты М_х и М_ъ в (7.Б.66):
М_, = Це}-е;)
71
Сравнивая (7.Б. З) с (7.Б.6), мы видим, каким образом параметры г] и /^.связаны с дисперсионной энергией Ел и эффективной энергией осциллятора Еео:
Е, = ье1-е:у/2
Р (7Б-9)
|
|
|
П = --------- ^-------- |
|
2 ЕЦЕ1-Е1) |
|
Е{эВ) |
|
Рис. 7.Б.2. е2в функции энергии фотонов в GaAs и его аппроксимация соотношением (7.Б.7) (воспроизведенная по Solid State comm. 15, М. А. Afromowitz. Refractive index of Ga, _ ^.Al^As, p. 59 (1974), с разрешения Elzevier Science). |
В самом деле, подставляя формулу для е2 (7.Б.7) в соотношение Крамерса - Кронига, мы в конце концов получаем:
|
Е}-Е2 |
![]() <?,(£■)= 1 + М.1+М_,Е2 + — 1п
<?,(£■)= 1 + М.1+М_,Е2 + — 1п
К
|
Е: - е2 |
![]() Е4 (7.Б.10)
Е4 (7.Б.10)
Соотношение Афромовича
Система уравнений (7.Б.8), (7.Б.9) и (7.Б. 10) позволяет рассчитать коэффициент преломления различных полупроводников (хорошо согласующиеся с экспериментальными значениями), как только определены значения Е&, Еео, Еа В таблице
7. Б.2 представлены значения этих параметров для трех трехкомпонентных соединений: АЮаАБ, ваАзР и Са1пР.
|
Табл. 7.Б.2. Эффективная энергия осциллятора Еео, энергия дисперсии ЕЛ и ширина запрещенной зоны Е& для различных полупроводниковых твердых растворов
|
На рис. 7.Б. З. представлены результаты расчета коэффициента оптического преломления в диапазоне составов твердых растворов АЮаА5.
|
3.8 3.7 3.6 3.5 3.4 3.3 |
|
X £ § А С I— X Ф =Г Ф -е В Л О |
|
3.2 |
|
|
1.2 1.3 |
|
1.4 1.5 1.6 Энергия фотона (эВ) |
|
1.7 1.8 |
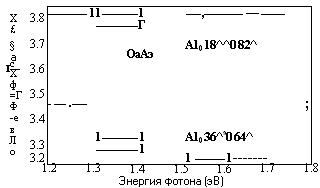 |
Рис. 7.Б. З. Коэффициент оптического поглощения в функции энергии фотонов для различных значений состава АЮаАБ, полученный с использованием формулы Афромовича (7.Б. 10).