Механика гидро - и пневмоприводов
Уравнения движения и неразрывности рабочих сред
Процессы в технических системах с гидро - и пневмоприводами во многом зависят от взаимодействия элементов приводов с рабочими средами. Для изучения этого взаимодействия применяют методы механики жидкости и газа, основанные на гипотезе сплошности рабочей среды, согласно которой среду рассматривают в макроскопическом масштабе, несоизмеримо превышающем расстояния между отдельными молекулами. В соответствии с такой физической моделью среда в отличие от системы материальных точек непрерывно распределена по занимаемому ею пространству, т. е. образует континуум. Математическое описание в указанном смысле сплошной среды может быть выполнено в переменных Эйлера и переменных Лагранжа. В первом случае движение среды определяют с
помощью величин, являющихся функциями пространственных координат и времени, причем необходимо учитывать, что через одну и ту же точку пространства в разные моменты времени проходят различные частицы среды. Во втором случае при описании движения среды используют величины, связанные с конкретными частицами, координаты которых заданы в начальный момент времени. Ввиду сложности уравнений, записанных в переменных Лагранжа, в механике жидкости и газа преимущественно применяют переменные Эйлера.
В связи с важностью уравнений, выражающих фундаментальные законы механики жидкости и газа, для дальнейшего освещения ряда вопросов механики гидро - и пневмоприводов ниже даны выводы этих уравнений, причем в дополнение к традиционному их изложению обращено внимание на особенности математического описания неустановившихся течений.
![]()
|
(I |
![]()
|
V |
![]() Уравнение движения среды (уравнение гидродинамики) основано на законе сохранения количества движения (импульса), согласно которому для ограниченного поверхностью 5 объема V среды имеем
Уравнение движения среды (уравнение гидродинамики) основано на законе сохранения количества движения (импульса), согласно которому для ограниченного поверхностью 5 объема V среды имеем
|
V 7 х5 |
Где и — вектор скорости движения центра массы среды, находящейся в объеме дУ р — плотность среды; Рт — вектор массовой силы, отнесенной к единице массы среды в объеме йУ] рп — вектор поверхностной силы, отнесенной к единице поверхности, ограничивающей объем (IV (напряжение поверхностных сил).
После деления на Л уравнение (2.10) принимает вид
^ I ipdV = I РтР + I Рп^5. (2.11)
V V 5
Левую часть уравнения (2.11) можно преобразовать путем дифференцирования интеграла, взятого по движущемуся в среде объему. Для этого возьмем два близких момента времени t и ^ = ^ + Д/. Условимся, что в момент времени t
А в момент времени ^ с учетом изменения V и ир до значений V' И (11/9У
|
= / («/>)'' V' :' = У (и р),4У+ I (ир)' (IV, |
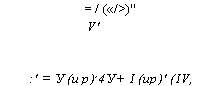 К' = JЫpУdV V'
К' = JЫpУdV V'
При малых А(
V У-У
Соответственно,
ДК = К'-К = 1[(ир)'~(ир)](1У+ I (ир)*ёУ
V У-У
С точностью до малых величин порядка не выше первого
(ир)' - ир= Д* +
Поэтому
V У'-У
Приращение V1 — V объема среды за время № допустимо считать равным dSunAt, где ип — проекция скорости точек поверхности 5 на внешнюю нормаль к ней. Учитывая это равенство, получаем
ДК = Д< I (IV+ Аг I(ир)'ип <1Б,
Отсюда находим
В последнем члене полученного выражения величина ир заменяет (ир) так как при переходе к производной At —> 0. Согласно формуле Гаусса - Остроградского, данный член можно представить в виде
/[ Г д д д
|
<IV |
![]() (ир) ип (ІБ = у I — (риих) + — (рииу) + — (рии2)
(ир) ип (ІБ = у I — (риих) + — (рииу) + — (рии2)
5 V
Подставляя это значение интеграла в предыдущее уравнение и учитывая ранее принятое соотношение для К, имеем
|
(IV |
![]() ) д(риих) д(рииу) д(рии2 У
) д(риих) д(рииу) д(рии2 У
Дх ду дг
V V
|
+ и ^1 + и ^- + и ^-+ Зі +их дх +иу ду +иг дг + |
![]()
|
Дих диу диг1 [с1(ри) V |
![]() ■Л //и(ж+р, іі''и)^ (212)
■Л //и(ж+р, іі''и)^ (212)
V V
Если в выделенном объеме среды отсутствуют источники и стоки, то последний интеграл в выражении (2.12) по условию неразрывности среды равен нулю. Тогда
V V
Соотношение (2.13) определяет важную для описания не - установившихся течений связь между изменениями во времени интегрального и местных значений количеств движения среды. Чтобы получить в дифференциальной форме уравнение движения среды, определим рп в последнем члене уравнения
(2.10) , выделив с этой целью в среде бесконечно малый тетраэдр ОАВС, каждая из трех граней которого перпендикулярна соответствующей оси декартовых координат, а положение четвертой задано нормалью п (рис. 2.8).
Рис. 2.8. Элементарный тетраэдр для определения напряжений в рабочей среде
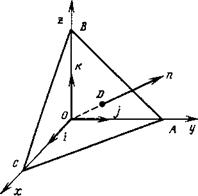 Обозначая Рд., ру, р2 и рп напряжения на гранях тетраэдра, имеющих нормали 1,$, к, п, и применяя уравнение (2.11) с учетом формулы (2.13), получаем
Обозначая Рд., ру, р2 и рп напряжения на гранях тетраэдра, имеющих нормали 1,$, к, п, и применяя уравнение (2.11) с учетом формулы (2.13), получаем
1Р^аУ = /Р”^- /рх^-
V V 5Х
J PydS - J + j рпйБ, (2.14)
5у Бг 5п
Где 5Х, 5У, 5* — проекции площади 5П грани АВС, т. е. = = 5П соб(71ж), Бу = 5П соз(пу), 5* = 5п соз(пг).
В соответствии с теоремой о среднем из уравнения (2.14) находим
Р ”7 3 _5пРпср
С05(п*)рхср - 5п СОБ(ггу)руср - 5П С08(п2)ргср, (2.15)
Где Н — высота ОБ тетраэдра. При Н —> О средние напряжения Рпср> Рхср> Руср> Р*ср в уравнении (2.15) стремятся к значениям напряжений в точке О, поэтому
Рп — Рх соБ(пх) + ру соБ(пу) + р2 со8(пг). (2.16)
Согласно уравнению (2.16) напряжение в точке О среды на произвольно ориентированной площадке можно найти по трем
напряжениям рх, руу р^, на площадках, перпендикулярных осям декартовых координат и проходящих через точку О. В свою очередь каждый из трех векторов Ря, рр2 можно представить тремя проекциями, вследствие этого напряжение в точке произвольно ориентированной площадки определяет тензор второго ранга
|
( |
Рхх Рху Рхг
Рух Руу Руг I = (Р{к)•
Ргх Ргу Ргг /
Первый индекс у компоненты тензора напряжений соответствует оси, перпендикулярной площадке, второй — оси, выбранной для вычисления проекции вектора напряжения.
Подставив в последний интеграл уравнения (2.11) рп из уравнения (2.16) и затем применив к этому интегралу формулу Гаусса — Остроградского, получим
J pndS = I[рх соб(пх) + ру соБ(пу) + р2 соБ(пг)] (18 =
V
С помощью соотношения (2.13) и уравнения (2.17) приведем уравнение (2.11) к виду
V
Интеграл (2.18) должен быть равен нулю при любом V что выполняется, если
/>— - оР +^Е£ + ??г + ^. Г2 194
Р а - рРт + дх + ду + а*' (219)
Уравнение (2.19) описывает неустановившееся движение сплошной среды в напряжениях, которые необходимо дополнительно определить. Для этого предварительно выбирают физическую модель среды. Достаточно общей является модель, учитывающая вязкость, сжимаемость и теплопроводность среды. Изотропную среду называют ньютоновской, если при ее
движении компоненты тензора напряжений будут линейными функциями тензора скоростей деформаций, а в покоящейся среде действуют только нормальные напряжения. К ньютоновским и близкими к ним средам относится большинство рабочих сред, используемых в приводах. Также широко применяют кремнийорганические жидкости, отличающиеся по своим свойствам от ньютоновских. Однако эти различия могут быть несущественными для гидродинамических процессов в приводах и прежде чем их учитывать, в каждом конкретном случае необходимо провести дополнительные исследования. Далее при изложении механики гидро - и пневмоприводов предполагается, что рабочие среды допустимо считать ньютоновскими. Для таких сред зависимость тензора напряжений от тензора скоростей деформаций имеет вид
|
Рху |
Pxz |
/1 |
0 0> |
||
|
Руу |
Pyz |
| = (-p+ Ai div u) |
° |
1 0 |
+ |
|
Pzy |
Pzz J |
Vo |
О 1, |
/ |
|
|
/ |
Јxx |
SXy |
Јxz |
||
|
+2 ц j |
Syx |
Јyy |
Јyz |
||
|
К Јzx |
Ezy |
Szz |
|
(2.20) |
![]() Где р — давление, которое равно взятому с обратным знаком среднему арифметическому трех нормальных напряжений, приложенных к трем взаимно перпендикулярным площадкам в данной точке среды, причем в общем случае к вычисленной таким образом величине прибавляют fiv div u; е— компоненты тензора скоростей деформаций; Ai — определяется соотношением:
Где р — давление, которое равно взятому с обратным знаком среднему арифметическому трех нормальных напряжений, приложенных к трем взаимно перпендикулярным площадкам в данной точке среды, причем в общем случае к вычисленной таким образом величине прибавляют fiv div u; е— компоненты тензора скоростей деформаций; Ai — определяется соотношением:
Ai = Hv ~ (2.21)
Для компонент тензора напряжений из уравнения (2.20) можно записать
Дих (дих диу
TOC o "1-5" h z Рхх = - р + А1 div и + 2ц —; рху = рух = ц + — J;
. Л диу (дия диг
Руу = ~Р + Aidivu + 2/i—; pyz = pzy = + — j;
, , „ duz (дих диЛ
Pzz = - р + Ai div u + 2ц —; р2Х = рХ2 = ц I I.
Компоненты рм при i ф к являются касательными напряжениями. Эти напряжения с одинаковыми, но расположенными в обратном порядке индексами будут попарно равны, что следует из равенства моментов относительно произвольной оси. Чтобы подчеркнуть их отличие от нормальных напряжений (рм при г = &), введем следующие обозна-
Чения: Рху Рух — т~ху т~ух j Pyz Pzy
Pzx ~ Pxz — TZX — Txz •
В таких обозначениях касательное напряжение при параллельно* струйном движении вязкой среды в направлении оси Ох в плоскости хОу выражает закон трения Ньютона:
Дит
Тух = Ц - Щ. (2.22)
Рассматривая совместно уравнения (2.19) и (2.20), получаем в проекциях на оси декартовых координат следующую систему уравнений движения вязкой сжимаемой среды:
|
+ |
|
+ Duz |
|
Dx Dux |
|
D +d~z |
|
Dz dx |
|
Dux п др д ( дих P~dr-pFi-fc+2dпV‘~fc ) +Jjl(/‘v-W3)divu]+^ |
|
( dux duy . % + аx ) _ К |
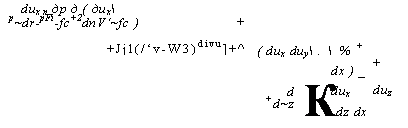
|
D ( duy ду V дУ ) |
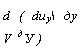 Duv dp
Duv dp
|
+ |
![]() P~dt-'>F’‘-Ty+i
P~dt-'>F’‘-Ty+i
|
+ Duz |
![]()
|
D +d~z |
![]()
Д d + ^K^-2n/3)divu} + —
( dux duy
V dy + dx ).
Dx
( duv duz
|
Duz !h |
|
+ D |
|
Duz dp d ( P~i-^~iz^d-zY |
|
+И ^v ~div + fa |
|
D |
|
Dux du. |
|
+ |
|
Dz dx |
 |
|
|
|
|
D_ + dy |
В левых частях этих уравнений стоят полные (индивидуальные) производные, которые можно записать в виде сумм локальных и конвективных ускорений среды:
|
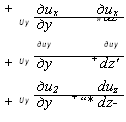
|
Dt dt dx Duy dtiy dtiy Ь ux |
![]() Dux дих дих --------- “ + их
Dux дих дих --------- “ + их
Dt dt dx
Duz _ duz duz
Dt dt Ux dx
Уравнения гидродинамики при p, v — 0, р = const были впервые выведены Навье (1827 г.) и Стоксом (1845 г.) Для невязкой среды (/х = 0, fly 0) уравнения гидродинамики получены в 1755 г. Эйлером, им же предложены уравнения, описывающие равновесие среды.
|
-/ Dtj |
![]() Уравнение неразрывности выражает закон сохранения массы среды. Этот закон при отсутствии в выделенном объеме
Уравнение неразрывности выражает закон сохранения массы среды. Этот закон при отсутствии в выделенном объеме
V среды источников и стоков можно представить в виде
PdV = 0. (2.23)
V
Дифференцирование интеграла (2.23), взятого по подвижному объему, выполняется тем же способом, который был рассмотрен в случае преобразования левой части уравнения (2.11). Но здесь величину ир следует заменить на р. После дифференцирования получаем
Равенство (2.24) справедливо для любого объема V, что возможно только в том случае, когда подынтегральная функция равна нулю. Согласно этому условию имеем уравнение
^ + р <Ну и = 0, (2.25)
Ис
Которое в механике жидкости и газа названо уравнением неразрывности (сплошности) Выразив (Ну и в проекциях на оси декартовых координат, уравнение (2.25) можно привести к виду
Dp, д{рих) d(puy) d(puz) _n
Di + ~~dT + ~di~ + ~dT - °- (2-26)
Если не учитывать сжимаемость среды, то при р = const из (2.26) будем иметь
Дих диу ди2 Л.
Дr + w+«r=0' (2'27)