Механика гидро - и пневмоприводов

Свойства рабочих сред

Из многих свойств рабочих сред, влияющих на разно­образные показатели гидро - и пневмоприводов, выделим толь­ко те, которые существенны для механики изучаемых приво­дов. К этим свойствам относятся плотность, вязкость, сжима­емость, теплоемкость и теплопроводность.

Плотность р жидкости или газа, заполняющих все рас­сматриваемое пространство, является функцией координат то­чек пространства и определяется соотношением

Р = Lim (1-25)

ДДV 4 '

Где Дга — масса среды, занимающей объем AV

В общем случае плотность р среды связана с давлением р и температурой 0 уравнением состояния

Др,/>,©) = 0. (1.26)

Плотность жидкостей по сравнению с газами в меньшей степени зависит от давления и температуры. Значения плот­ности (кг/м3) воздуха и некоторых жидкостей приведены ни­же:

TOC o "1-5" h z Воздух при 0°С 1,29

Вода при 4 °С 1000

Жидкость AM Г-10 850

Масло АУ 886 — 896

Масло индустриальное 20 880 — 890

Керосин при 38 °С.......................... 790

Вязкость проявляется в сопротивлении среды относи­тельному сдвигу ее слоев. Мерой этой вязкости среды служит динамическая вязкость /х или связанная с ней кинематическая вязкость I/:

/г = ру. (1-27)

Вязкость жидкостей с увеличением температуры умень­шается, а газов возрастает, что вызвано их различным молеку­лярным строением. Приближенная зависимость динамической вязкости жидкости от температуры имеет вид

М1 = М2^), (1-28)

Где ц и /Л2 — значения динамической вязкости жидкости при температурах ©1 и ©2, взятых здесь в °С; значения величины с для минеральных масел, применяемых в гидроприводах, лежат в пределах от 2,53 до 3,27.

У большинства жидкостей вязкость увеличивается с ро­стом давления в соответствии с соотношением

Ц = (1-29)

Здесь /х и /хо — значения динамической вязкости жидко­сти при давлении р и атмосферном давлении соответственно, значения Ь для минеральных масел равны 0,02... 0,03 1/МПа.

При больших скоростях объемной деформации среды уве­личивается диссипация механической энергии, что связано с проявлением объемной вязкости. Отношение значений объем­ной вязкости к динамической вязкости /х составляет для минеральных масел /х^//х = 1,33 при /х = 0,21 Пас.

Сжимаемость жидкостей и газов проявляется в измене­нии занимаемого средой объема в зависимости от давления. Эта зависимость для жидкостей слабее, чем для газов, что в ряде случаев позволяет жидкости считать несжимаемыми. Од­нако известно также много примеров колебательных процессов в трубопроводах, неустойчивости гидроприводов и других ди­намических явлений, связанных с сжимаемостью жидкостей. Зависимость объема среды от давления определяется соотно­шением

Ау = - А:*™?, (1.30)

Где V — объем среды, (3сж — коэффициент сжимаемости сре­ды.

Изменение объема среды сопровождается изменением ее плотности, поэтому

(1р = (Зсжр(1р. (1.31)

Вместо коэффициента сжимаемости среды применяют также обратную величину

В = ТГ> (132)

ИСЖ

Которую называют модулем объемной упругости среды.

Модуль объемной упругости, или коэффициент сжимае­мости среды, находят либо экспериментальным путем, либо с помощью формул (1.30)—(1.31). При использовании второ­го способа необходимо еще иметь уравнение состояния среды. Если средой служит газ, который обычно принимают совер­шенным, то можно воспользоваться уравнением Клапейрона

Р = рЛ0, (1.33)

Где О — температура, К; Я — газовая постоянная, для воздуха Л = 287,14м2/(с2-К).

При интенсивном теплообмене между газом и окружаю­щей элементы привода средой процесс изменения состояния га­за будет близким к изотермическому; из формул (1.31)—(1.33) следует, что изотермический модуль объемной упругости газа равен

Вн. г — Р•

Если теплообмен незначительный, то изменение состояния газа будет близким к адиабатическому и тогда

= const, (1.35)

Р

Где к = cv/cv — показатель адиабаты; (ср — удельная тепло­емкость газа при постоянном давлении; cv — удельная тепло­емкость газа при постоянном объеме; для воздуха к = 1,4).

Применяя формулы (1.31), (1.32) и (1.35), найдем соотно­шение, определяющее адиабатический модуль объемной упру­гости газа:

(1.36)

Уравнение термодинамического состояния жидкости по­лучить значительно сложнее, чем для газов. Известно не­сколько подходов к выводу такого уравнения, не исключаю­щих, однако, необходимости привлечения экспериментальных данных. Вследствие этого на практике чаще используют зна­чения модулей объемной упругости жидкостей, полученные экспериментальным путем. Для одной и той же жидкости его значения будут зависеть от условий, в которых проводил­ся эксперимент, и способа обработки результатов измерений. Если модуль объемной упругости определялся при постоянной температуре жидкости, то его называют по аналогии с моду­лем объемной упругости газа изотермическим, а если условия проведения эксперимента позволяют пренебречь теплообменом между жидкостью и окружающей средой, — адиабатическим. Изотермический и адиабатический модули разделяют на име­ющие средние значения и локальные значения. Средний изо­термический модуль объемной упругости жидкости находят, подставляя результаты измерений в формулу

(1.37)

Где Ар — разность между конечным и начальным давлениями, при которых начальный объем Уо жидкости изменился на Д V

Средний адиабатический модуль объемной упругости жидкости определяют с помощью формулы такого же вида, как (1.37), но используют при этом результаты экспериментов, проведенных в условиях адиабатического изменения состояния жидкости.

Локальный изотермический модуль В” ж объемной упру­гости жидкости получают в результате обработки эксперимен­тальных данных по формуле

Аналогичную формулу применяют для определения ло­кального адиабатического модуля В^ж объемной упругости жидкости при соответствующих этому виду модуля экспери­ментах.

Для используемых в гидроприводах жидкостей в диапа­зоне значений рабочих температур 0 170° С и давлений до

80 МПа зависимость локального изотермического модуля объ­емной упругости от давления можно представить в виде

<ж = «ж)о + Ю,6р, (1.39)

Где (Ри. ж)о — локальный изотермический модуль объемной

Упругости жидкости при атмосферном давлении.

Приближенную зависимость локального адиабатического модуля объемной упругости от давления можно описать урав­нением

Яа. ж = (Я"ж)о + 12,5р, (1.40)

Где (5а. ж)о — локальный адиабатический модуль объемной

Упругости жидкости при атмосферном давлении.

Нестационарные гидродинамические процессы по сравне­нию с тепловыми процессами, как правило, протекают значи­тельно быстрее, что позволяет в динамике приводов приме­нять локальный адиабатический модуль объемной упругости жидкости, обозначая его Вж.

Рассмотренные зависимости модулей объемной упругости жидкостей от давления основаны на экспериментах, выполнен­ных с жидкостями, не содержащими нерастворенный газ. Од­нако рабочие жидкости гидроприводов часто содержат нерас­творенный воздух и если при заполнении устройств гидропри­вода жидкость не подвергается вакуумированию, то она будет представлять собой смесь жидкости и газа. Такая же смесь мо­жет образовываться в гидроприводах во время динамических процессов из-за разных скоростей растворения и выделения га­за при падении давления на отдельных участках течения ра­бочей среды. Чтобы оценить влияние нерастворенного газа на значения модуля объемной упругости рабочей жидкости, вы­делим объем жидкости Уж 5 в котором находятся пузырьки воз­духа объемом Ув. Изменение объема смеси Усм = Уж + Ув при изменении давления равно

(1УСМ = (1УЖ + <1УВ. (1.41)

В соответствии с формулами (1.30) и (1.32)

Уж <Пгж = —і2-<ір,

“ж

<ІУв = -^<ір,

“в

Где модуль объемной упругости Вв воздуха может быть как изотермическим, так и адиабатическим.

Подставив 6УЖ и вУв из соотношений (1.42) и (1.43) в урав­нение (1.41), получим

(1.44)

Соотношение (1.44) представим в виде

(1.45)

Модуль объемной упругости Всм в соотношении (1.45), со­гласно (1.44), определяется формулой

(1.46)

В

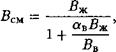В реальных условиях объем пузырьков воздуха, содержа­щегося в жидкости, значительно меньше объема самой жидко­сти, поэтому принимаем Усм = Уж и приводим формулу (1.46) к виду

(1.47)

Где ав = Ув/Усм — объемное содержание воздуха в жидкости.

На термодинамический процесс изменения состояния пу­зырьков воздуха влияют их размеры, равномерность распре­деления в жидкости, теплоемкость и теплопроводность жид­кости, а также скорость изменения давления в смеси. В свя­зи с неопределенностью влияния достаточно большого числа факторов проведем оценку отличия Вси от Вж по наихудшему
из возможных вариантов, принимая изотермическое значение Вв = р. В этом случае при р — 10 МПа, Вж — 1450 МПа, аъ = 0,001, по формуле (1.47) находим Всм 1266 МПа. С увеличением давления влияние нерастворенного воздуха на модуль объемной упругости смеси уменьшается. Кроме то­го, при больших давлениях вследствие растворения воздуха в жидкости уменьшается ав, что также способствует приближе­нию значений Всм к Вж.

При изоэнтропийных процессах локальный адиабатиче­ский модуль объемной упругости воздуха связан со скоростью св распространения звука соотношением

Да. г = Рс в - (!-48)

Учитывая уравнение (1.33), формулу (1.48) запишем в ви­де

Св = ZkRQ, (1-49)

Скорость ссм звука в смеси жидкости с равномерно рас­пределенными пузырьками воздуха найдем, используя форму­лы (1.46) и

Вс м = Рсмссм> (1.50)

Где рсм — плотность смеси.

После несложных преобразований получаем

В»

Рсм(1 - ав) (1 + вкрж^

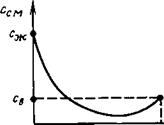
Согласно (1.51) скорость ссм имеет минимум между зна­чениями ав = 0 и ав = 1 (рис. 1.28). Это означает, что ско­рость звука в смеси жидкости с воздухом будет меньше, чем в жидкости без нерастворенного воздуха и чем в самом воздухе. Последнее объясняется тем, что инертность среды в основном определяет жидкость, а упругость — воздух. Приближенной моделью такой среды может служить система тел с массами, определяемыми плотностью жидкости, и упругими связями в виде воздуха.

Рис. 1.28. Зависимость скорости звука в смеси жидкости с воздухом от объемного содержания воздуха

О ( ОС*

Теплоемкость рабочих сред характеризуется количест­вом теплоты, которое необходимо для повышения температу­ры среды на один градус Кельвина. В справочниках обычно указана отнесенная к единице массы среды теплоемкость сш, называемая удельной. Для минерального масла при темпера­туре 15°С ст = 1,88 2,09кДж/(кг*К).

Теплопроводность рабочих сред определяет количество теплоты, переносимое через единицу площади поверхности, выделенной в среде, за единицу времени при перепаде темпе­ратур в один градус Кельвина. Эту величину называют ко­эффициентом кТ теплопроводности среды. Теплопроводность газов возрастает с увеличением температуры, а жидкостей — падает. Для воздуха кт = 0,023 Вт/(м-К), для минерального масла при температуре 15°С кт = 0,14 Вт/(м*К).