Механика гидро - и пневмоприводов

Силы трения при движении рабочих сред в зазорах элементов гидро — и пневмоприводов

В гидро - и пневмоприводах между деталями, которые должны перемещаться относительно друг друга, имеются тех­нологические зазоры. Чтобы исключить утечки рабочей сре­ды, во многих устройствах применяют контактные уплотне­ния. При таких уплотнениях возникают силы сухого трения, которые могут привести к снижению точности управления устройством. По этой причине в регулирующих и направляю­щих аппаратах контактные уплотнения на подвижные детали

Обычно не ставят, а для уменьшения утечек назначают пре­дельно малые технологические зазоры. При наличии в зазоре рабочей среды на детали будут действовать силы давления и силы вязкого трения. Кроме этих сил, когда рабочей средой служит минеральное масло, могут действовать силы, вызван­ные сложным физико-химическим явлением, при котором про­исходит облитерация (заращивание) зазора.

Еще в 50-х годах при испытаниях регуляторов гидро­энергетических установок автором было обнаружено, что че­рез некоторое время после подачи масла под давлением зна­чительно увеличиваются силы, необходимые для начальных смещений цилиндрических золотников в осевом направлении, и почти до нуля уменьшаются утечки по зазорам золотни­ковых устройств. На поверхностях золотников разобранных устройств были замечены потемневшие места. Результаты этих испытаний во многом соответствовали полученным при­близительно в те же годы данным об облитерации зазоров зо­лотниковых пар, применявшихся в различных областях техни­ки. Однако как само явление, так и причины возникновения значительных сил сопротивления перемещению золотников до сих пор не имеют достаточно обоснованных объяснений.

Предположительно облитерацию зазора можно объяснить тем, что содержащиеся в масле добавки образуют на поверх­ности металла пленки, неравномерно покрывающие стенки за­зора. Вследствие этого нарушается распределение давления в зазоре и возникают силы, прижимающие одну деталь к дру­гой. Продолжающийся процесс образования пленок вызыва­ет уменьшение зазора, сопровождается увеличением неравно­мерности распределения в нем давления и соответствующим увеличенем силы, которая необходима для начального смеще­ния одной из деталей. Для выравнивания давлений на цилин­дрических поверхностях обычно делают кольцевые канавки, но они не спасают от облитерации большую часть зазора и в этом отношении недостаточно эффективны. Известно, что пу­тем создания высокочастотных колебаний или вращения одной из деталей практически полностью устраняется облитерация зазора. В связи с этим последние два способа долгое время
широко применяли в различных гидроаппаратах. В результа­те совершенствования конструкций и технологии изготовления золотниковых устройств, а также улучшения свойств рабочих жидкостей эти способы используют все реже.

Независимо от того, имеет место или нет облитерация за­зора пока образующие его стенки находятся в покое, после на­чала движения одной из них течение жидкости подчиняется законам гидромеханики. В этих случаях, а также в тех, когда

Рабочей средой служит газ, для расчета сил давления и сил

Вязкого трения необходимо знать режим течения среды в за­зоре. Для определения режима течения подсчитывают число Рейнольдса, подставив предварительно в формулу (3.8) значе­ние смоченного периметра

X* = 2 Ъ (3.61)

И площадь проходного сечения зазора

Бг = М, (3.62)

Где Ъ и 6 — ширина стенок и расстояние между ними (зазор) соответственно.

С учетом соотношений (3.61) и (3.62) формула (3.8) при­нимает вид

2 6у

Яе* =----- .

V

Для реальных элементов гидро - и пневмоприводов зна­чения параметров в формуле (3.63), при которых число Рей­нольдса будет максимальным, можно принять следующими: Ь = 0,05 мм, V = 50 м/с, V 0,1см2/с. В этом случае Ле2 = 500. Критическое значение Кекр, указывающее на пере­ход в зазоре ламинарного режима течения в турбулентное, обычно получается больше 2000, поэтому допустимо предпола­гать, что в зазорах элементов гидро - и пневмоприводов течения рабочих сред будут преимущественно ламинарными. Кроме режима течения важно еще знать, при каких условиях можно пренебречь инерцией среды, если рассматриваются нестацио­нарные процессы в гидро - или пневмоприводах. Чтобы найти такие условия, проведем оценку порядка членов в уравнениях

Рис. 3.9. Местные скорости течения в зазоре между плоскими неподвижными стенками (а) и в зазоре с одной движущейся стенкой (б)

Навье-Стокса. Пренебрегая сжимаемостью среды, для тече­ния в зазоре с плоскими стенками достаточно записать одно уравнение (рис. 3.9):

Дих д2их 1 др

=~?Т*’ (3б4)

Где их — местная скорость при неустановившемся движении среды в зазоре.

Для сравнения членов уравнения (3.64) выберем масшта­бом времени характеризующее рассматриваемый процесс вре­мя Г, а масштабом координаты у — расстояние 6 между стен­ками зазора. При таких масштабах члены в левой части урав­нения имеют соответственно следующий порядок:

О -5Г =■£; №

■№)-

Где О — обозначение порядка величины (от латинского огс1о — порядок).

Соотношения (3.65) и (3.66) показывают, что первым чле­ном уравнения (3.64) можно пренебрегать по сравнению со вто­рым, если

£»?• (зб7>

При выполненном условии (3.67) инерция среды мало вли­яет на неустановившееся течение, которое в таком случае до­пустимо заменить квазистационарным течением. Например,
если V = 0,1см2/с, 6 = 0,05 мм, то имеем 1//62 = 4000 с“1, что соответствует частоте колебаний среды в зазоре, равной 637 Гц, которая значительно превышает частоту колебаний, возникающих в реальных гидро - и пневмоприводах.

Выше были рассмотрены течения среды в зазоре за преде­лами начального участка, в котором происходит формирование профиля местных скоростей (рис. 3.9, а). Длину /нач начально­го участка при ламинарном течении определяют так, чтобы в конце этого участка максимальные скорости в формирующем­ся профиле и в параболическом профиле отличались не более чем на 1 % Для вычисления /нач служит соотношение

/нач = 0,026Ке2, (3.68)

По которому при 8 = 0,05 мм Ке2 = 500 получаем /нач = = 0,5 мм.

Зазоры между золотниками и гильзами у современных ги­дроаппаратов составляют несколько микрон, в таких устрой­ствах начальный участок может повлиять только на утечки жидкости, причем вблизи средних положений золотников.

Касательные напряжения в рабочей среде на стенке зазо­ра возникают как при движении одной стенки относительно другой, так и при движении среды под действием разности да­влений перед зазором и после него. При ламинарном устано­вившемся движении среды за пределами начального участка в зазоре с параллельными стенками уравнение (3.64) можно привести к виду

Д2их др. .

= (3'69)

Где // = ри — динамическая вязкость среды.

Без учета изменения вязкости среды вследствие изменения ее температуры имеем

| = (*.то)

Здесь р и Р2 — давления перед зазором и после него; I — длина зазора.

Подставив правую часть соотношения (3.70) в уравнение (3.69), получим

<™>

Дважды интегрируя уравнение (3.71), находим функцию, описывающую распределение местных скоростей по сечению зазора:

Их = ~~2цР у2 + ^1У (~'2' (3.72)

Предположим, что нижняя (рис. 3.9, 6) стенка зазора не­подвижна, а верхняя — перемещается со скоростью ист па­раллельно нижней стенке. Направив ось х посередине зазора, запишем следующие граничные условия:

Их = 0 при у = (3.73)

Их - ±«ст при У = +-• (3-74)

Здесь знак соответствует перемещению стенки по напра­влению движения среды, совпадающему с положительным на­правлением оси х. Определив при граничных условиях (3.73) и (3.74) постоянные С и С2, функцию (3.72) представим в виде

Р Р2 /Л осх2 2 I ^ст, ^ст /л 7г

Пх = ~2’ -2Г)±—у±—. (3.75)

Чтобы найти касательные напряжения в потоке среды, подставим функцию (3.75) в уравнение, выражающее закон вязкого трения Ньютона:

(з-7б)

После дифференцирования функции и выполнения всех не­обходимых алгебраических операций получаем

Т = (3.77)

Из формулы (3.77) следует, что касательное напряжение на движущейся стенке, для которой у = (5/2, определяется

(Р1 - Р2) 6 М«СТ

21 ^ 6

Умножив обе части соотношения (3.78) на площадь кон­тактирующей со средой поверхности движущейся стенки, на­ходим приложенную к стенке со стороны потока силу вязкого трения

(Р1 - Р2)6Ь цЫ

Ытг Т —

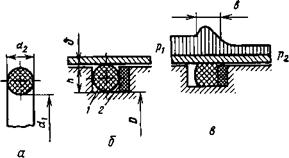
Где Ъ — ширина стенки; если стенками зазора служат две круг­лые цилиндрические поверхности, то, учитывая малость вели­чины <5, можно принимать Ь = 7г^, здесь (I — диаметр одной из цилиндрических стенок зазора.

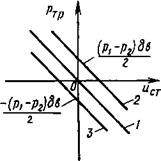
Рис. 3.10. Зависимость силы вязкого трения от скорости движения стенки и разности давлений в концевых сечени­ях зазора

На рис. 3.10 даны графики для трех случаев: р = Р2 (пря­мая I), р > Р2 (прямая 2), р < Р2 (прямая 3). Графики 2, 3 показывают, что при неподвижной стенке (мст = 0) и наличии течения среды вследствие действия разности давлений перед зазором и после него сила вязкого трения отличается от ну­ля, причем в зависимости от направления течения в зазоре эта составляющая силы трения может помогать движению или со­здавать сопротивление движению стенки. С уменьшением ве­личины 6 зазора составляющая силы вязкого трения, возника­ющая при течении среды из-за разности давлений, уменьша­ется, а составляющая, вызванная движением стенки, — увели­чивается.

В исполнительных гидро - и пневмодвигателях приводов для уменьшения утечек рабочих сред по зазорам с подвиж­ными элементами применяют контактные уплотнения. При таких уплотнениях, как было отмечено выше, на подвижные элементы действуют силы сухого трения. Если рабочей средой является вязкая жидкость, то благодаря тонкому смазывающе­му слою на поверхности элемента трение может быть смешан­ным. Рассмотрим силы трения, которые возникают в часто применяемых уплотнениях с резиновыми кольцами, имеющи­ми круглое поперечное сечение. Резиновое кольцо диаметром (1 (рис. 3.11, а) размещено в кольцевой канавке диаметром 2}, выполненной на подвижном элементе (например, на поршне). Размеры кольца выбирают так, чтобы диаметр был несколь­ко меньше 2}, а диаметр йч — обеспечивал образование на кольце контактной поверхности шириной &1, необходимой для герметичности уплотнения за счет предварительной деформа­ции кольца 1 в канавке (рис. 3.11, б). Для защиты кольца от выдавливания в зазор при действии высокого давления р со стороны низкого давления Р2 устанавливают защитную шай­бу 2 из материала более твердого (обычно из фторопласта), чем резина. Если при работе устройства давление р2 может быть больше р1, то защитные шайбы устанавливают с двух сторон резинового кольца.

Под нагрузкой, создаваемой разностью рн = Р~Р2 давле­ний, происходит дополнительная деформация резинового коль­ца, и ширина контактной поверхности увеличивается до значе­ния 6, одновременно изменяется эпюра контактного давления (рис. 3.11, в). Силы смешанного трения в таких уплотнениях вычисляют по формуле

Рсм. пр — 7г/)/б1рк#Ср, (3.80)

Где / — коэффициент трения; рк. Ср — контактное давление (среднее значение).

Коэффициент трения / зависит от рн, скорости движения стенок уплотняемого зазора относительно друг друга шерохо­ватости их поверхностей и твердости резины, из которой изго­товлено кольцо. При разном сочетании перечисленных факто­ров коэффициент трения может иметь значения от 0,008 до 0,3. Ширина контактной поверхности при отсутствии давления за­висит от твердости резины и степени ее сжатия после уста­новки уплотнения. Приближенно эта величина определяется соотношением

Ьг =0,03 <*2е, (3.81)

Где Ь в мм; е — относительное сжатие резинового кольца, для уплотнения, устанавливаемого на движущейся детали, равно 0,10...0,25.

Среднее контактное давление тоже приближенно можно найти по формуле

Рк. ср = 1,25еЯ1(Г2 + ср. (3.82)

Здесь Е — модуль упругости резины, 10 ..20 МПа; с — коэффициент передачи резиной давления на стенку, равный 0,85.. 1,0 при р в МПа.

После длительной (1 час и более) неподвижности эле­мента с уплотнением коэффициент трения увеличивается до

0, 8... 1,0, что вызывает увеличение силы, необходимой для начального смещения элемента. В общем виде изменение си­лы трения в зависимости от скорости ист перемещения эле­мента можно представить приведенным на рис. 3.12 графиком. Штриховыми линиями на рисунке показано, как изменится си­ла трения при появлении жидкостного трения в уплотнении,

Рис. 3.12. Зависимость создавае­мой уплотнением силы трения от скорости движения стенки зазора

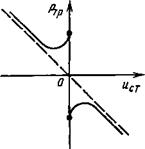Нагруженном давлением 15 ... 20 МПа при ист = 1... 2 м/с. Однако при таких скоростях уплотнение может разрушиться или, во всяком случае, значительно сократится срок его рабо­ты.