Механика гидро - и пневмоприводов

Расчет нагрузок на выходные звенья гидро — и пневмоприводов

При взаимодействии с объектом выходное звено приво­да нагружено силами и моментами сил, возникающими из-за инерции перемещаемого устройства объекта, а также вызван­ными приложенными к этому устройству силами и момента­ми сил со стороны окружающей среды и других устройств. В зависимости от вызывающих нагрузку причин ее называют позиционной, трением и инерционной. Позиционную нагрузку создают силы и моменты сил, значения которых изменяют­ся при изменении положения перемещаемого приводом устрой­ства. Трение подразделяют на сухое, гидро - или газодинами­ческое и смешанное.

Для расчета инерционной нагрузки предварительно вы­числяют приведенные к выходному звену значения массы или момента инерции перемещаемого устройства так, чтобы со­блюдалось равенство кинетических энергий перемещаемых и приведенных масс. Другие виды нагрузки находят исходя из равенства работ сил или моментов сил, приложенных к выход­ному звену и перемещаемому приводом устройству.

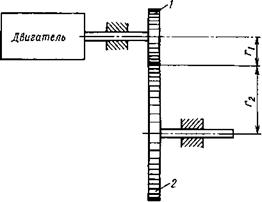
Если выходное звено привода и перемещаемое устройство соединены посредством какого-либо механизма (зубчатого или рычажного), то параметры нагрузок являются функциями пе­редаточного числа г механизма. Для примера рассмотрим зуб­чатый механизм (рис. 2.2), состоящий из шестерни 1, которая закреплена на валу исполнительного гидро - или пневмодвига­теля, и шестерни 2, вал которой непосредственно соединен с перемещаемым устройством. Передаточное число г такого ме­ханизма определяется отношением угловых скоростей вала ис­полнительного двигателя и вала перемещаемого устройства. Значение г можно также вычислить с помощью отношения 7*2/п радиусов делительных окружностей или отношения ко­личества зубьев у шестерен 2 и 1. Приравнивая кинетические

Энергии и работы без учета диссипации энергии в зубчатом механизме, получаем

Т _ J2' и _ ^тр2 и _ &поз2

^1 — *2 ! *тр1 — ^2~’ ^поз1 — *2 >

% % % где — отнесенный к валу 1 исполнительного двигателя момент инерции; 3^ — момент инерции вращаемого валом 2 устройства; &хр 1, &хр2, &по31 и кпо32 — коэффициенты трения и позиционных нагрузок, отнесенные к валу 1 (отмечены ин­дексом 1) и к валу 2 (отмечены индексом 2).

Аналогично можно найти параметры нагрузок, действую­щих на выходное звено с возвратно-поступательным перемеще­нием. Отличие состоит только в том, что в этом случае вместо моментов инерции необходимо пересчитать значения поступа­тельно перемещающихся масс и нагрузки представить прило­женными к выходному звену силами, а не моментами сил.

Нагрузки на выходное звено привода можно описать функ­циями, связывающими угловую скорость П выходного звена или скорость V его поступательного перемещения с моментом М сил или суммарным значением сил, равным Р Такие функ­ции описывают состояние нагрузки на выходном звене при про­исходящих в приводе динамических процессах. По ним при из­

Вестном законе движения выходного звена могут быть постро­ены графики нагрузок. Исходными для определения состояния нагрузки служат уравнения движения выходного звена, кото­рые в линейном приближении записывают в виде

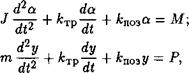(2.1)

(2.2)

Где а, у — угловое и поступательное перемещения выходно­го звена привода соответственно; «/, т — момент инерции и масса, отнесенные к выходному звену привода; &тр — коэф­фициенты трения, возникающего при вращательном или по­ступательном движении выходного звена привода; кпоз — ко­эффициенты позиционной нагрузки, действующей на выходное звено привода.

При гармонических колебаниях выходного звена

Где аа и ау — амплитуды колебаний выходного звена; и — угловая частота колебаний.

Поскольку каждое из уравнений (2.1) и (2.2) с учетом со­ответствующих им соотношений (2.3) и (2.4) по форме явля­ются одинаковыми, достаточно найти функцию, описывающую состояние нагрузки, для одного из двух выходных звеньев, на­пример для звена с поступательным перемещением. Используя формулу (2.4), получаем

(2.5)

Уравнение (2.2) в случае гармонических колебаний выход­ного звена принимает вид

О •

Р = —тауи втсЛ + кТ^у + кпозау вто;/.

Из уравнений (2.5) и (2.6) нетрудно найти

V

---- = совиЛ;

Ауи

TOC o "1-5" h z Р к'Тт/1) . .

——------ 2—^ = ипа;*. (2.8)

Ау{кпоз - гтш*)

Просуммировав взятые в квадрат соотношения (2.7) и (2.8), получим

(Р — ктт>у)2 у2 , ч

--- ^-------- ±Е__'------ 1______ — 1 (О О')

ау(кпоз - гпи2)2 (ауи)2

Если в уравнении (2.9) Р заменить на М, V — на П, т — на 7, ау — на аа, то будем иметь уравнение состояния нагрузки на выходное звено с угловым перемещением.

Графиком, построенным в координатах РОу или МОП по уравнению вида (2.9), является эллипс, часть которого показа­на на рис. 2.3.

Гармонические колебания выходного звена имеют место, например, в приводах испытательных установок, или при ис­следовании динамических характеристик привода. В тех слу­чаях, когда по условиям использования привода законы дви­жения его выходного звена значительно отличаются от гармо­нических, может быть построен график нагрузки с учетом за­данной циклограммы работы привода и требуемого вида пере­ходных процессов при смене выполняемых приводом операций.

Рис. 2.4. Характерные точ­ки для определения нагрузок на выходное звено привода

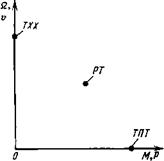Часто вместо графика нагрузки для расчета привода задают значение скорости движения выходного звена, которое необхо­димо обеспечить при действующей на него нагрузке. Такая рабочая точка (РТ) показана на рис. 2.4. Кроме того, могут быть заданы скорость движения выходного звена в отсутствие нагрузки (точка холостого хода ТХХ) и максимальная нагруз­ка при полном торможении выходного звена (точка ТПТ).