Механика гидро - и пневмоприводов

Применение общих принципов механики в расчетах гидро — и пневмоприводов

Современные гидро - и пневмоприводы в общем случае представляют собой совокупность взаимосвязанных и взаи­модействующих механических, гидравлических, пневматиче­ских, электромеханических и электронных устройств. Эти до­статочно сложные системы являются составными частями бо­лее крупных технических систем, в которые входят различные управляемые объекты. Примерами таких объектов могут слу­жить роботы и манипуляторы, технологические и транспорт­ные машины, энергетические установки, летательные аппара­ты и др.

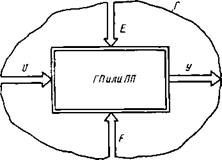
При проектировании и использовании гидро - и пневмо­приводов их выделяют из всей технической системы с учетом тех требований, которые должны быть выполнены для осу­ществления управления заданными объектами. Чтобы иметь возможность рассматривать гидро - и пневмоприводы в зна­чительной мере независимо от особенностей того или иного объекта, в дальнейшем будем придерживаться схемы, изобра­женной на рис. 2.1. На схеме показаны: канал управляющих и воздействий на гидропривод (ГП) или пневмопривод (ПП), канал наблюдения за величинами У описывающими движе­ние выходного звена привода, канал поступления энергии Е в привод и канал возмущающих Р воздействий. Вне грани­цы Г в управляемом объекте или в системе более высокого ие­рархического уровня указанные каналы могут взаимодейство­вать, что отражается в математическом описании 17, ^ и

При формулировании требований к гидро - или пневмоприво­ду. По физическому содержанию и соответствует либо элек­трическим, либо механическим величинам в зависимости от схемы и конструкции привода; Е — мощность потока рабочей среды, поступающей к приводу от источника энергопитания; У — перемещения (поступательные или угловые) штока или вала исполнительного двигателя; Р — может быть вызва­но различными причинами (действием сил реакций в местах крепления элементов приводов, действием электромагнитных полей в окружающем привод пространстве, вибрациями и пе­реносным движением конструкции, с которой связан привод, колебаниями давления рабочей среды и т. п.).

Заметим, что граница Г в значительной мере условна. На­пример, приток энергии Е можно характеризовать не мощно­стью рабочей среды, а мощностью, подводимой к двигателю, вращающему вал насоса или компрессора источника энергопи­тания привода. В таком случае при расчете процессов, про­текающих в приводе, необходимо учитывать процессы в дви­гателе, если частота вращения его вала зависит от мощности, потребляемой насосом или компрессором. Вид закономерно­стей управляющих воздействий зависит от назначения приво­да и способов управления объектом, которые необходимо осу­ществить с помощью привода.

С точки зрения теоретической механики гидро- и пнев­моприводы являются системами материальных тел с неголо - номными нестационарными связями. Такие связи обусловлены наличием в приводе сжимаемой рабочей среды и упругих ме­ханических звеньев, соединяющих отдельные детали привода. Применяя принцип освобождаемости от связей, их действие заменяют силами, приложенными к деталям привода со сто­роны рабочей среды и упругих механических звеньев. После этого используют с той или иной степенью полноты уравнения движения твердых тел, уравнения движения, энергии, нераз­рывности и состояния рабочей среды, а также уравнения, опре­деляющие силы в упругих звеньях. Кроме того, могут потре­боваться уравнения, описывающие тепловые процессы в при­воде. Перечисленные уравнения образуют основу математиче­ской модели привода, которую необходимо дополнить уравне­ниями и функциями, характеризующими физические свойства рабочих сред, конструктивные параметры элементов приводов и указанные выше воздействия на привод.

Элементы гидро - и пневмоприводов часто достаточно про­извольно расположены один относительно другого, что не­сколько усложняет выбор координат, определяющих переме­щения элементов в пространстве. С целью упрощения матема­тических моделей приводов равновесие и движение отдельных элементов рассматривают обычно в своих координатах, нача­ло которых выбирают так, чтобы ему соответствовало одно из равновесных состояний привода. Связь между координа­тами всех элементов получается в результате решения систе­мы уравнений, составляющих математическую модель при­вода. Чтобы согласовать направления перемещений элемен­тов, измеренных в своих координатах, положительными можно принять направления, при которых движение выходного зве­на привода происходит в принятом для него положительном направлении. В некоторых случаях положительным считают такое направление перемещения выходного звена привода, ко­торое вызывает увеличение параметров управляемого объек­та. Независимый выбор систем координат для каждого эле­мента позволяет в математическом описании протекающих в них процессов пользоваться как декартовыми, так и цилин­дрическими или сферическими координатами. При этом обя­зательно выполнять все положения теоретической механики об использовании инерциальной системы координат и коорди­нат, связанных с движущимся объектом, если в нем размещен привод.