Механика гидро - и пневмоприводов

Колебательное и апериодическое звенья второго порядка

Уравнения звеньев второго порядка имеют вид

Г2§+2ст!+!'=*“- <4ло1>

Где Т — постоянная времени; С — коэффициент относительно­го демпфирования; К — коэффициент усиления.

Звено называют колебательным при 1 > £ > 0, а при £ > 1

— апериодическим. Эти термины связаны с типом переход­ного процесса, вызванного скачком входного сигнала. Такой процесс можно рассчитать, решив непосредственно дифферен­циальное уравнение (4.101) или применив передаточную функ­цию звена

Щ*) = о о К-------------- • (4.102)

^ ' Г2з2 + 2(Тз + 1 v ’

При и =1(<) изображение входного сигнала 11(з) = 1/з. В этом случае

УМ=^ = №гЬттт)- (4103)

Корни знаменателя передаточной функции (4.102), т. е. ее по­люсы, для колебательного звена находят по соотношениям

51 = - а + ;а;с, 52 = - а - ;и;с,

В которых

С

А=-, ис =--------- ------ .

При некратных корнях 51, 52 можно, как и при определении переходной функции апериодического звена первого порядка, воспользоваться формулой (4.85). Здесь

М(0) = К; М(зк) = К; П(0) = 1;

Ь($) = 2Т2и^ -0(^2) = -2Т2ш^,

Поэтому переходная функция колебательного звена имеет вид

У(0 = К+ :e<-“+**>4

2 (—Q J^c) T ucj

+------------- —------------- e-(«+jvc)t (4 104)

2 (—a — ju>c) (—T2ucj) l4,iU4J

Вторая и третья составляющие переходной функции (4.104) являются комплексно сопряженными выражениями, сумма которых равна удвоенной вещественной части одного из них:

2ДеГ7-------- К sm9 • * =

2 (-a + juc) T2ucj

- К - ~ Т*ис а2 + <л>%

Ke~at

Re[(-uc + ja) (coswc t + j sin wci)] =

T2wc(a2 + u%)

Ke~at

(uic cos u>ct + asinWcO =

T2uc(a2 + a;2)

= — Кe~at ^cosuct + — sinwci). (4.105)

С учетом выражения (4.105) переходная функция (4.104) принимает вид

1-

Е at( cos uct + — sin uct )

WC ).

Переходной функции (4.106) можно придать другой вид, умно­жив и разделив выражение в круглых скобках на віпу> при V? = a, тctg(uc/a) и применив формулу для синуса двух углов. В результате получим

У(і) = К[ — Ае~аі 8Іп(и;сі + у*)]) (4.107)

Где

A=^— = Jl + sin<p у

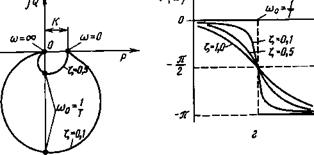
Построенный по формуле (4.106) или (4.107) переходный процесс является колебательным затухающим (рис. 4.9, а, кри­вая 1). Интенсивность затухания процесса оценивают по отно­шению а/а2 амплитуд, взятых в моменты времени, отличаю­щиеся на период 2тт/ис колебаний. По формуле (4.107) находим величину

(4.108)

Которую в теории колебаний называют логарифмическим де­крементом затухания.

При С > 1 полюсы передаточной функции (4.102) будут действительными числами и соответственно переходный про­цесс станет апериодическим (рис. 4.9, а, кривая 2).

Частотные характеристики колебательного и апериодиче­ского второго порядка звеньев определяют путем подстановки

З = Зи ъ передаточную функцию (4.102). В результате полу­чают АФЧХ

Т^тктг - <4Л09>

Формулу (4.109) можно записать в виде

= Р{и) + і<2{и),

Где

К( 1 - и2Т2)

Р^ = (1 — а;2Т2)2 + (2£и;Т)2 ’ ^4Л1°^

^ = "(1-а;2Г2)2 + (2(шТ)2' ^4'П^

Для значений и, изменяющихся от 0 до оо, АФЧХ колебатель­ного звена изображена на рис. 4.9, б.

Амплитудную и фазовую частотные характеристики вы­числяют соответственно по формулам:

^/(1 - о;2Т2)2 + (2С^Т)2 ’

Я(ы)

<р(и) = arctg

2Са>Т

~ ~агс*ё ['_игТ2' ыТ <\ (4.113)

СНи)

Р(ы) = аГ^ - р^у - 7Г =

2СиТ

= ~ аГС^ Ь^Т2 ” Ж’ иТ>1- (4.114)

Логарифмическую амплитудную характеристику, с уче­том того, что Ь(ш) = 20 ^ Л(ш), нетрудно найти из формулы (4.112) в виде

Цы) = 20 %К- 10^[(1 - и2Т2)2 + (2Си;Т)2]. (4.115)

Как и в случае апериодического звена первого порядка, по­лезными для расчетов являются уравнения асимптот харак­теристики (4.115) при низких (иТ < 1) и высоких (иТ > 1) частотах. Для первой асимптоты:

Ьі{и) = 20^К, (4.116)

Для второй асимптоты:

12(и) = 20]%К - 40%иТ (4.117)

Вычисляя по уравнению (4.117) значения і2(и;,Т) и і2(10а;,Т) при > 1/Т, замечаем, что наклон второй асим­птоты составляет — 40 дБ/дек.

При К = 1 первая асимптота совпадает с осью частот. Обе асимптоты пересекаются в точке, где и = = 1/Т

(рис. 4.9, в). Характеристика (4.115) по-разному отклоняется от своих асимптот в зависимости от коэффициента относи­тельного демпфирования. При 0 < С < 1 (колебательное звено) это отклонение будет максимальным при резонансной частоте:

У/1 - 2С2 (4.118)

Если С = 0, то характеристика имеет разрыв при о;р = шц. Таким образом, у колебательного звена есть три характерных частоты: резонансная, собственная частота колебаний при пе­реходном процессе

Ь>с = щу/і - С2 (4.119)

И собственная частота в отсутствие демпфирования (С = 0)

«о = (4.120)

При С > 1 колебательное звено превращается в аперио­дическое второго порядка звено, логарифмические амплитуд­ные характеристики которого располагаются ниже своих асим­птот. Чтобы получить логарифмические амплитудные харак­теристики при К > 1 или К < 1, следует построенную для К = I характеристику сместить на 201 %К вверх, если К > 1, и вниз, если К < 1. Вместо смещения характеристики можно
в противоположные указанным направлениям переносить па­раллельно самой себе ось частот. Фазовые характеристики не зависят от значения К и изменяются только при изменении £ (рис. 4.9, г).

Устройство, которое было рассмотрено как интегрирую­щее и апериодическое первого порядка звенья, может служить также примером колебательного или апериодического второ­го порядка звеньев, если присоединить к поршню тело мас­сой т. В значении 771 может учитываться и масса поршня (рис. 4.10, а). Кроме того, примем, что при движении поршня на него действует сила Ртр вязкого трения. Уравнение движе­ния поршня при таких условиях имеет вид

$Уп

771-^2“ ““ $пРц ~ Рпр

Перемещение поршня, как и в предыдущих примерах, будем измерять от положения, при котором РПр = Рпро, а силу вяз­кого трения представим соотношением

Р - к ^ тр “ тр м ’

Где ктр — коэффициент вязкого трения (см. § 3.5).

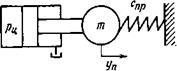
Рис. 4.10. Гидромеханическое устройство (а) и элек­трический контур (5) как примеры звена второго по­рядка

После подстановки в уравнение (4.121) выражений, опре­деляющих РПр И Ртр, приведем его к виду

TOC o "1-5" h z ш ^2Уп, ^тр (^Уп спр __ (л 100ч

5п 5П Л 5п Уп ~Рп Рц0’ ^ ^

Где

^пр О РцО “ “75 •

*Эп

Из линеаризованной функции (4.96) следует, что

Рц = й,0 + %^- (4.123)

КЯр

Расход ф среды, если по-прежнему не учитывать ее сжима­емость, определяет уравнение (4.71), воспользовавшись кото­рым, из уравнения (4.123) находим

*5п ^2/п

Рц РцО ту' ту - Л+ ’ л др аъ

Подставив это значение рц в уравнение (4.122), получим

Я* ^2Уп /&тр 5П <1уп спр «о /. 10/,ч

!й + Х** ~ Тц,- (4124)

Разделив все члены уравнения (4.124) на коэффициент при уп>

Запишем результат в форме уравнения (4.101):

7,2 ж+2СТ^+Уп = (4125)

Где

Гг

1 = л — — постоянная времени устройства;

V спр

С2

И I П р К

С = — — коэффициент относительного демпфиро-

2- у/тспр вания;

5

Ку(} =---- ^------ коэффициент преобразования расхода сре-

Спрл<?р ды в перемещение поршня.

В формулу для коэффициента £, от численного значения которого зависит, является ли данное устройство колебатель­ным или апериодическим звеном второго порядка, входят ко­эффициенты ктр и Kqp. Последний коэффициент, согласно уравнению (4.96), связан с параметрами клапана и характе­ризует изменение его пропускной способности в зависимости от давления рц. Диссипация энергии возрастает с увеличени­ем ктр. Постоянная времени Т представляет собой величину, обратную частоте uq недемпфированных колебаний тела мас­сой га, которая соединена с пружиной жесткостью спр. По­добные устройства в теории колебаний называют линейными осцилляторами с одной степенью свободы.

Электрический контур, динамические характеристики ко­торого будут такими же, как у колебательного или апериоди­ческого звена второго порядка, состоит из катушки с индук­тивностью X, резистора, имеющего омическое сопротивление Л, и конденсатора емкостью С (рис. 4.10, б). Для такого кон­тура

V-2 — и — L - jj - — Ric• (4.126)

A t

С учетом, что гс = приведем уравнение (4.126) к виду

Dt

Ж+ Ж7^ +”’ = “>• (4Д27)

Вводя обозначения Т = у/LC и ( = 0, bR^/C/L, можем урав­нение (4.127) записать в форме уравнения (4.101).

В начале § 4.3, кроме рассмотренных звеньев, были назва­ны еще форсирующие звенья первого и второго порядков, пе­редаточные функции которых будут обратными по отношению к передаточным функциям апериодического первого порядка, колебательного и апериодического второго порядка звеньев со­ответственно. Их частотные характеристики находят теми же способами, которые были описаны ранее, причем логариф­мические амплитудные и фазовые частотные характеристики форсирующих звеньев можно построить путем изменения на­клона асимптот в области высоких частот с отрицательных на положительные при одновременной замене отрицательных знаков у значений фаз на положительные.

Заметим, что при реальных физических процессах всегда имеют место явления, вследствие которых изменение выход­ной величины происходит с некоторым отставанием по вре­мени от входного воздействия, поэтому передаточные функ­ции технически осуществимых устройств при наличии в них форсирующих звеньев будут содержать еще интегрирующие, апериодические или колебательные звенья. Вносимые этими звеньями искажения частотных характеристик зависят от их параметров. Если параметры выбраны так, что форсирую­щие звенья в основном определяют частотные характеристики в выбранном диапазоне частот, то такие звенья относятся к реально форсирующим. Именно этого вида звенья применя­ют при корректировании разнообразных систем управления, включая системы с гидро - и пневмоприводами.