Механика гидро - и пневмоприводов
Гидродинамические силы и их расчет для сопла-заслонки и клапана
Гидродинамические силы действуют на обтекаемые рабочей средой элементы гидро - и пневмоприводов. Эти силы, как и рассмотренные выше гидростатические силы, определяются интегралом, взятым по поверхности от приложенных к ней в местах контакта с рабочей средой напряжений. В общем
случае напряжения могут быть представлены нормальными и касательными к поверхности составляющими. Соответственно гидродинамические силы подразделяют на силы давления и силы трения.
При вычислении гидродинамических сил наиболее сложно найти функции, которые описывают распределение напряжений по поверхностям тел, обтекаемых рабочей средой. В связи с чем расчеты чаще всего выполняют, привлекая дополнительно к теоретическим соотношениям экспериментальные характеристики. Сначала познакомимся с методами расчета сил давления, так как для изложения расчета сил трения потребуется еще обсудить закономерности течений в зазорах между подвижными и неподвижными элементами.
Силы давления можно найти двумя методами. Согласно первому, предварительно вычисляют действующую на элемент гидростатическую силу, которую затем умножают на коэффициент, полученный экспериментальным путем. В таком расчете используют соотношение
-Ргд — ^ГД-РгС) (3.25)
Где Ртд — гидродинамическая сила давления; Ртс — сила гидростатического давления; &гд — коэффициент, учитывающий действительное распределение давления среды на поверхности обтекаемого тела.
Коэффициент А;гд зависит от формы обтекаемого рабочей средой тела, его относительных размеров, числа Рейнольдса при установившемся движении среды, а при неустановившемся движении — от критериев, характеризующих вид и параметры процесса. При известных значениях &гд расчет по формуле (3.25) достаточно прост, так как силу Ртс нетрудно определить с помощью уравнений равновесия рабочей среды. Однако вследствие влияния многих факторов на &гд его значения в большинстве случаев заранее известны только для конкретных конструкций устройств, работающих при заданных условиях, что ограничивает возможности распространения полученных результатов на другие устройства.
Более общими могут быть расчеты, выполненные в соответствии со вторым методом, который основан на теореме об изменении количества движения среды, протекающей сквозь выделенный неподвижной поверхностью 5 объем V Согласно этой теореме запишем следующее уравнение:
^ J pudV + j рмип dS = Ру + Р5 + Рт, (3.26)
V 5
Где и — вектор местной скорости среды; ип — проекция вектора скорости на нормаль к поверхности 5; Ру — вектор массовых сил; Р5 — вектор сил давления и трения на поверхности 5; Рт — вектор сил, приложенных к среде со стороны обтекаемого ею тела.
Левая часть уравнения состоит из суммы изменяющегося во времени количества движения среды, находящейся в объеме V, и количества движения среды, проходящей через поверхность 5. В правую часть уравнения входят силы, которые приложены к выделенному объему среды. Если тело не целиком находится внутри выделенного объема, то та часть его поверхности, которая соприкасается со средой, будет частью поверхности 5. При этом вектор Р5 следует вычислять, не учитывая силы, действующие на среду со стороны указанной части поверхности тела, так как они составляют силу Рт.
Применим уравнение (3.26) для расчета гидродинамических сил, выбрав, с одной стороны, достаточно часто используемые в гидро - и пневмоприводах элементы, а с другой — позволяющие наглядно представить метод расчета. К таким элементам можно отнести сопло-заслонку, клапан и золотник. Вначале рассмотрим сопло-заслонку и клапан.
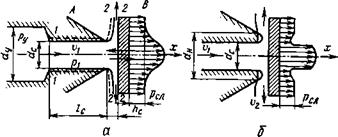
Сопло-заслонка. Схема потока среды, вытекающей из сопла А, частично прикрытого плоской заслонкой В, дана на рис. 3.4, а. При истечении среды в пространство, в котором та же среда находится под давлением рСЛ больше атмосферного, распределение давления на поверхности заслонки будет близким к показанному на рисунке.
Штриховой линией выделим в потоке границы объема и укажем контрольные сечения 1-1 и 2-2, через которые среда соответственно втекает в выделенный объем и вытекает из него. Примем, что давления и скорости в живых сечениях
|
Рис. 3.4. Схема течения рабочей среды в устройстве сопло - заел онка |
Потока, совпадающих с контрольными сечениями, распределены равномерно, а размеры заслонки по сравнению с диаметром отверстия в сопле настолько велики, что скорость У2 направлена по нормали к оси сопла. Кроме того, не будем учитывать массовые силы, инерцию среды после ее истечения из сопла и силы трения на поверхности, ограничивающей выделенный объем. При перечисленных допущениях, следуя приведенной выше теореме, запишем в проекциях на ось х уравнение количества движения в виде
= $сР1 ~ $сРсл ~ Рз. С, (3.27)
Где бг1, У и р — массовый расход, скорость среды и давление в сечении 1-1; 5С — площадь проходного сечения сопла, при круглом цилиндрическом сопле, 5С = тг^с/4; Р3.с — сила воздействия заслонки на вытекающий из сопла поток.
Гидродинамическая сила Ргд, приложенная со стороны потока к заслонке, равна и противоположна по направлению силе Р3.с, что позволяет по уравнению (3.27) найти
РГд = 5с(р1 — Рсл) + 0у — 1С ^ • (3.28)
При установившемся движении среды последний член в уравнении (3.28) будет равен нулю, им можно также пренебречь при малой длине /с* В этих случаях
РГд = 5с(Р1 — Рсл) + £*1^1- (3.29)
Уравнение (3.29) показывает, что действующая на заслонку гидродинамическая сила несколько превышает гидростатическую силу, определяемую первым членом в правой части этого уравнения. Такое дополнительное воздействие среды на заслонку происходит вследствие поворота потока, который сопровождается расширением на поверхности заслонки области повышенного давления (рис. 3.4, а). Для вычисления гидродинамической силы Ргд необходимо знать давление р, массовый расход С?! и скорость у. Перечисленные величины связаны с давлением ру в камере перед соплом, давлением рсл после сопла, а также зависят от расстояния Лс между соплом и заслонкой. Скорость движения среды в камере перед соплом обычно можно считать пренебрежимо малой по сравнению со скоростью в самом сопле.
При истечении газа для вычисления скорости применяют формулу (3.11), в которую подставляют: р = р, ро = ру, ^ РО = Ру = Ру/(Д0у), где ©у — температура газа в
Камере перед соплом. После такой замены величин имеем
SHAPE \* MERGEFORMAT ![]()
К/(к-1)
|
(3.30) |
![]()
|
Р1 = Ру |
![]() ■ (к-1^1 2кЯ&у
■ (к-1^1 2кЯ&у
Значение скорости VI по условию сохранения массы для протекающей по соплу среды должно также удовлетворять соотношению
Р8су = £с. (3.31)
Массовый расход газа через сопло, прикрытое заслонкой, определяется по формулам (3.20) и (3.22) после замены в них величин с помощью соотношений:
£др - С* £др = £с, Ра = Ру У
Коэффициент расхода /хс либо выбирают на основании экспериментальных данных, либо назначают равным 0,7 .0,8. Для
Круглого цилиндрического сопла 5др = 7гйсЛс. Учитывая малые размеры сопла по сравнению с размерами камеры перед
Ним, при определении значения плотности р газа можно принять, что температура 01 газа в сечении 1-1 равна температуре газа 0у в камере перед соплом. При таком допущении по уравнению (3.14) находим
Л = Щ - <3'32>
С помощью соотношения (3.32) формулу (3.31) представим в виде
Сгс-Й0у
”1 = ~Й$Г' (333)
Уравнение (3.30) после подстановки в него из соотношения
(3.33) запишем в виде
(3'34)
Таким образом, в случае течения газа для вычисления гидродинамической силы Ртд, действующей на заслонку, выполняются следующие операции. Сначала при выбранном значении Лс по формулам (3.20) и (3.22) находят значение массового расхода Сгс. Затем решают уравнение (3.34) относительно р и по соотношению (3.33) определяют VI. Полученные значения Рь Са = бгс и подставляют в формулу (3.29).
Если рабочей средой служит малосжимаемая жидкость, то расчет несколько упрощается, так как плотность среды можно принять постоянной. При установившемся движении среды, не учитывая пока сопротивление на входе в сопло и по-прежнему пренебрегая скоростью среды в камере перед соплом, по уравнению Бернулли находим
Р1=Ру - ^Г - (3.35)
Скорость вычислим по расходу жидкости, значения которого, согласно условию неразрывности течения, будут одинаковыми на участке между сечениями 1-1 и 2-2 (см. рис. 3.4, а) и поэтому
Ос
С
Где <2с — объемный расход жидкости, вытекающей из прикрытого заслонкой сопла; 5С — проходное сечение сопла, равное
5Г<^/4.
![]() Сопло вместе с зазором между его торцом и заслонкой представляет собой короткий канал с дросселем, следовательно, для определения расхода фс можно применить формулу (3.7). С учетом того, что здесь <2 = С}с, /хдр = /хс, £др = = 7ГЙСЛС, ра = Ру, РЪ = рсл, запишем эту формулу в виде
Сопло вместе с зазором между его торцом и заслонкой представляет собой короткий канал с дросселем, следовательно, для определения расхода фс можно применить формулу (3.7). С учетом того, что здесь <2 = С}с, /хдр = /хс, £др = = 7ГЙСЛС, ра = Ру, РЪ = рсл, запишем эту формулу в виде
(3.37)
Коэффициент /хс расхода учитывает гидравлическое сопротивление всего канала от камеры перед соплом, в которой давление равно ру, до камеры с давлением рсл. Значения этого коэффициента близки к 0,7...0,8 при числах Рейнольдса
11е = VI(1С/и = 2 104. Объемный фс и массовый С расходы
|
(3.38) |
![]() Через прикрытое заслонкой сопло связаны соотношением
Через прикрытое заслонкой сопло связаны соотношением
После подстановки в формулу (3.29) определяемых соотношениями (3.35)-(3.38) величин и получаем
|
|
По формуле (3.39) можно оценить отличие гидродинамической силы от гидростатической, действующей на заслонку, когда она полностью закрывает сопло (Лс = 0). Отношение Лс/^с в реальных устройствах составляет 0,1... 0,25, а среднее из указанных выше значение /хс равно 0,75. При этом гидродинамическая сила Ргд будет больше гидростатической в 1,09 .. 1,56 раза.
В схеме, принятой для расчета гидродинамической силы, поток рабочей среды не соприкасается с торцом сопла. Такая картина течения имеет место при острой кромке у выходного отверстия сопла. В случае притупленной кромки вытекающий из сопла поток может “прилипнуть” к торцу сопла и тогда
вблизи выходной кромки сопла в потоке образуется сжатое сечение, в котором давление будет меньше рсл (рис. 3.4, б). Если рабочей средой является жидкость, то из-за снижения давления в зазоре между торцом сопла и заслонкой возможно возникновение неустойчивого кавитационного течения, при котором гидродинамическая сила будет периодически изменяться, что приведет к колебаниям заслонки. Для устранения этих колебаний повышают давление рсл.
|
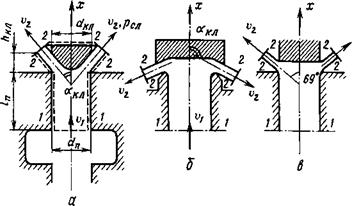
Рис. 3.5. Влияние формы клапана на углы истечения рабочей среды: а — а < 90°, б — а > 90°, в — а = 69° |
Клапан. Гидродинамическая сила, действующая на клапан, определяется почти так же, как в случае сопла-заслонки. Отличие главным образом вызвано тем, что поперечный раз - мер йкл (рис. 3.5, а) близок к поперечному размеру (диаме - ТРУ ^п) канала, по которому рабочая среда подводится к клапану. Вследствие этого направление течения среды после клапана может отклоняться от его оси на угол акл, не равный 90°. В связи с чем уравнение количества движения, записанное в проекциях на ось, совпадающую с осью клапана, будет содержать проекцию количества движения рабочей среды после клапана. Заметим, что для сопла-заслонки аналогичная проекция количества движения среды обратилась в нуль, так как течение среды направленно вдоль заслонки по нормали к оси сопла.
В остальном можно повторить рассмотренные выше шаги по вычислению гидродинамической силы, представив ее при установившемся движении среды в виде
Ртд — (Рп ~ Рсл) + GKjiV — GKJlV2 cos акл, (3.40)
Где Ргд — гидродинамическая сила, действующая на клапан; Рп и Рсл — давления в камере перед входом в подводной канал клапана и на сливе после клапана; 5П — площадь проходного сечения подводного канала клапана; Скл — массовый расход среды, пропускаемой клапаном; v и v<i — скорости среды в сечениях 1-1 и 2-2 соответственно.
Если рабочей средой является газ, то при использовании формул для расчета массового расхода и скоростей среды необходимо принять:
Сцр = £*кл) £*др — Ра ~ Рпч Pb — Рсл>
©а — № др — ^кл> *$др — $кл-
Г рафики зависимости коэффициента расхода /хкл клапана от числа Рейнольдса и относительных размеров клапана похожи на графики таких же зависимостей, приведенных на рис. 3.2 для золотников. Для клапанов число Рейнольдса находят с помощью соотношения (3.8), подставляя в него вычисленные с учетом формы клапана его площадь проходного сечения и смоченный периметр. Ориентировочные значения /хкл равны 0,8 при Re > 2 • 104. Площадь проходного сечения 5КЛ (рис. 3.5, а) определяется соотношением
*$кл — ^dnhKJi sin а:Кл, (3.41)
Где Лкл — высота подъема клапана над седлом.
При установившемся движении малосжимаемой жидкости уравнение (3.40) можно привести к виду
Ргд, ~ (Рп ~ Рсл) Sn + pQxn{vl ~ v2 COS 0;кл), (3.42)
Где р — плотность жидкости; <2кл — объемный расход жидкости через клапан.
Величины, которые входят в уравнение (3.42), вычисляют с помощью соотношений:
Используя соотношения (3.41) и (3.43) - (3.45) уравнение (3.42) можно также записать в виде (3.25):
|
(3.46) |
![]() ^ГД — (Рп ~ Рсл) 8цКкл,
^ГД — (Рп ~ Рсл) 8цКкл,
Где
![]()
|
БШ (X кл. |
Из формулы, определяющей коэффициент Ккл, и уравнения
(3.46) следует, что на гидродинамическую силу существенно влияет угол акл между вектором скорости среды после клапана и осью клапана. При Икл < 4 и углах акл менее 90° значения Ккл будут меньше единицы, поэтому вычисленная по формуле (3.46) гидродинамическая сила получается меньше гидростатической силы, равной (рп — рсл) 5П. Если клапан и его седло выполнены так, как показано на рис. 3.5, б, то угол акл будет превышать 90°, соответственно, значение Ккл становится больше единицы, а гидродинамическая сила — больше гидростатической.
При некоторых формах клапана и седла течение после клапана может быть отрывным (рис. 3.5, в). С изменением относительного подъема Лкл/^п такого клапана отрывное течение переходит в течение с прилипанием потока либо к седлу, либо к клапану. Смена режимов течения среды сопровождается периодическими изменениями гидродинамической силы, что вызывает колебания клапана.