Механика гидро - и пневмоприводов
Апериодическое звено первого порядка
Этот тип звена можно описать уравнением
Т^ + У = Ки (4.80)
Или соответствующей уравнению (4.80) передаточной функцией
Иг«=ггЬ (4'81)
Где К — коэффициент усиления (преобразования); Г — постоянная времени.
Переходную функцию, определяющую отклик (реакцию) апериодического звена на скачок входного сигнала и = 1(2), получают либо путем решения уравнения (4.80), либо с помощью передаточной функции (4.81). В первом случае используют известный из математики метод решения неоднородных дифференциальных уравнений при начальном условии у(0) = 0. Во
Втором — сначала функцию 1(2) заменяют ее изображением
И(з) = (4.82)
А затем находят изображение
После подстановки в соотношение (4.83) правой части передаточной функции (4.81) изображение выходного сигнала принимает вид
![]() (4.84)
(4.84)
![]() Для определения функции-оригинала у(2) по изображению У (5) используют формулу разложения Хевисайда
Для определения функции-оригинала у(2) по изображению У (5) используют формулу разложения Хевисайда
(4.85)
Где з*. — корни уравнения £*(з) = 0;
|
|
Для передаточной функции (4.81) и изображения (4.84):
М(0) = М(ак) = К, п = 1, = ^ = т,
Поэтому
У(0 = К +---- ----- е~*/Т = К (1 - е_1/г). (4.86)
|
|
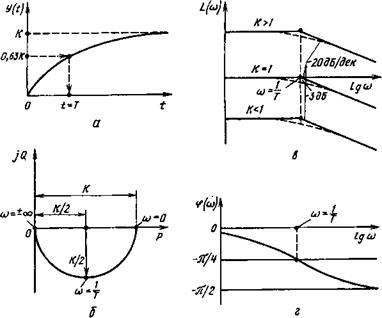
График переходной функции (4.86) для апериодического звена первого порядка приведен на рис. 4.7, а. В данном случае процесс, вызванный ступенчатым изменением входного сигнала (скачком - м), является апериодическим, чем и объясняется название данного звена. Если такой график получен при испытаниях какого-либо устройства, то по нему можно определить постоянную времени Г, которая равна значению t в тот момент времени, когда у = 0,63К. В этом легко убедиться, подставив в формулу (4.86) t = Т
![]() Амплитудно-фазовую частотную характеристику апериодического звена описывает функция, полученная подстановкой $ — в передаточную функцию (4.81):
Амплитудно-фазовую частотную характеристику апериодического звена описывает функция, полученная подстановкой $ — в передаточную функцию (4.81):
(4.87)
|
Рис. 4.7. Переходная (а), амплитудно-фазовая частотная (б), логарифмические амплитудная (в) и фазовая (г) характеристики апериодического звена |
Выделяя вещественную Р(и) и мнимую части, формулу
(2.87) представляем в виде
Тг_.. ч К КиТ. .
^ “ 1 + (ыТ)2 ~ 3 1 + (иТ)г ( *
При изменении и от 0 до +оо АФЧХ, построенная по уравнению (4.88), будет полуокружностью с центром в точке Р(и) = = К/2, Ої(ш) = 0 (рис. 4.7, б).
Амплитудную частотную характеристику апериодического звена можно найти как модуль в виде
А{и) = к/^[ї+{йту, (4.89)
А фазовую частотную характеристику, как аргумент
Ір(и) = — а, ТСІ£шТ
|
(4.90) |
![]() Логарифмическую амплитудную характеристику определяют с помощью формулы (4.89):
Логарифмическую амплитудную характеристику определяют с помощью формулы (4.89):
Цы) = 20^Л(ы) = 20&К - 101^1 + (ыТ)2]. (4.91)
Эта характеристика имеет две асимптоты, уравнение первой из них можно получить, подставив в формулу (4.91) и = 0 и записав результат в виде
|
(4.92) (4.93) |
![]() Ьі{и) = 2Ь%К. Уравнение второй асимптоты (4.91) имеет вид Ь2{и) = 2ЩК -2ЩиТ
Ьі{и) = 2Ь%К. Уравнение второй асимптоты (4.91) имеет вид Ь2{и) = 2ЩК -2ЩиТ
Обе асимптоты показаны на рис. 4.7, в сплошными линиями. Приближающаяся к асимптотам точная логарифмическая характеристика (4.91) нанесена штриховой линией. Наибольшее отклонение точной характеристики от асимптот составляет —3 дБ при и = 1/Т
Логарифмическая фазовая характеристика апериодического звена первого порядка, построенная по уравнению (4.90), изменяется в пределах от 0 до — 7г/2, проходя через точку (р(и) = —7Г/4 при и = 1/Т (рис. 4.7, г).
![]() Примером апериодического звена первого порядка может служить устройство с поршнем, который нагружен силой Рпр> создаваемой пружиной жесткостью спр (рис. 4.8, а). Пренебрегая, как в предыдущем случае, массой поршня и силами трения, найдем давление в полости цилиндра
Примером апериодического звена первого порядка может служить устройство с поршнем, который нагружен силой Рпр> создаваемой пружиной жесткостью спр (рис. 4.8, а). Пренебрегая, как в предыдущем случае, массой поршня и силами трения, найдем давление в полости цилиндра
(4.94)
Предположим, что при некотором положении поршня сила пружины равна Рпр о. Измеряя от этого положения перемещение 2/п поршня, представим уравнение (4.94) в виде
|
П |
(4.95)
Рис. 4.8. Гидромеханическое устройство (а) и электрический контур (б) как примеры апериодического звена
Где рцо = ^про/^п — давление в полости цилиндра при начальном положении поршня.
|
(4.96) |
![]() Соотношение (4.95) показывает, что в результате действия силы на поршень пружины давление в полости цилиндра изменяется при перемещении поршня, поэтому разность давлений рп - Рц в формуле (4.72) является переменной величеной. Если остальные члены в правой части формулы принять постоянными, то график изменения расхода ф в зависимости от рц будет нелинейным (рис. 4.8, б). Чтобы линеаризовать полученную для расхода ф функцию, проведем в точке 0; касательную и ограничим используемый при расчете участок графика прямыми 1-1 и 2-2. После такой аппроксимации зависимость расхода ф от давления рц в полости цилиндра становится линейной:
Соотношение (4.95) показывает, что в результате действия силы на поршень пружины давление в полости цилиндра изменяется при перемещении поршня, поэтому разность давлений рп - Рц в формуле (4.72) является переменной величеной. Если остальные члены в правой части формулы принять постоянными, то график изменения расхода ф в зависимости от рц будет нелинейным (рис. 4.8, б). Чтобы линеаризовать полученную для расхода ф функцию, проведем в точке 0; касательную и ограничим используемый при расчете участок графика прямыми 1-1 и 2-2. После такой аппроксимации зависимость расхода ф от давления рц в полости цилиндра становится линейной:
![]()
|
Д(^ ЦклЬклхкл |
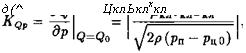
|
Где |
Причем коэффициент Кс}Р взят по модулю, так как его отрицательный знак учтен в уравнении (4.96).
Подставив (2 из (4.96) в (4.71), получим
^п-^- = <Зо - КЯр(рп-р11о). (4-97)
Из уравнений (4.95) и (4.97) находим
Разделив все члены уравнения (4.98) на коэффициент при уп, запишем полученное уравнение в форме (4.80)
Т^ + Уп = КудЯ о, (4.99)
Где Т = Зп/{КдрСпр) — постоянная времени рассмотренного устройства; Куд = 8ц/(Кдрспр) — коэффициент преобразования расхода среды в перемещение поршня.
Таким образом, перемещение уп нагруженного пружиной поршня будет изменяться после включения расхода фо в соответствии с динамическими характеристиками апериодического звена, если справедливы допущения, принятые при выводе уравнения (4.99).
Электрический контур, состоящий из резистора и конденсатора, также может служить примером апериодического звена первого порядка (рис. 4.8, в). Записав известные из электротехники уравнения
42 = и- гсК и гс = С - т-,
Аъ
Найдем
ЛС^ + «2 = иь (4.100)
Где ЛС = Т (Т — постоянная времени, Л — сопротивление резистора, С — емкость конденсатора); гс — электрический ток в контуре.