ЖЕЛОБКОВЫЕ КОЛЕБАНИЯ РАЗРЕЖЕННОЙ ПЛАЗМЫ С НЕОДНОРОДНЫМ ДРЕЙФОМ ИОНОВ
С. В. ПУТВИНСКИЙ, А. В. ТИМОФЕЕВ
Введение
Известно, что в плазме, помещенной в открытые магнитные ловушки, появляются новые коллективные степени свободы — желобковые колебания. При малой плотности плазмы, когда выполняется условие гцг>аН (г* — дебаевский радиус ионов, а — радиус плазмы, Я — характерный масштаб изменения магнитного поля), желобковые колебания разделяются на три ветви: электронную, ионную и так называемую вармовскую [*• *]. В аксиально-симметричных системах желобковые колебания представля
|
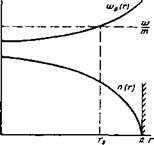
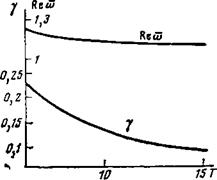
Рис. 1. Зависимость частоты желобковых колебаний от плотности плаз - кы, * — ионная ветвь, е — электронная ветвь, и — вармовская ветвь, Л* — критическая плот |
|
Ность |
|
|
 |
|
|
Ют собой волны, бегущие по азимуту. Зависимость фазовой скорости колебаний от плотности плазмы схематически изображена на рис. 1. С ростом плотности фазовая скорость ионной ветви уменьшается от й)0 до ([42]/г) 0)*,
А электронной — возрастает от 0 до О/2) ©<>. Здесь ©<> =----------------------------
Т{(й{гН
|
И слабо зависит от плотности плазмы. Эта ветвь колебаний может оказаться неустойчивой, если распределение ионов по энергиям имеет достаточно сложный вид (имеет два максимума [*]). Ионная и вармовская ветви желобковых колебаний обязаны своим появлением неоднородности магнитного поля, которая вызывает азимутальный дрейф ионов. Однако, по нашему мнению, влияние неоднородности магнитного поля на желобковые колебания до сих пор учитывалось |
![]()
|
(1) |
![]() Угловая скорость дрейфа ионов, — ионная циклотронная частота, е — энергия ионов, Я (г) — магнитное поле. При критической плотности, когда выполняется условие гл2«аД, ионная и электронная ветви желобковых колебаний сливаются и плазма становится неустойчивой [*]• Фазовая скорость третьей ветви желобковых колебаний близка к угловой скорости дрейфа ионов
Угловая скорость дрейфа ионов, — ионная циклотронная частота, е — энергия ионов, Я (г) — магнитное поле. При критической плотности, когда выполняется условие гл2«аД, ионная и электронная ветви желобковых колебаний сливаются и плазма становится неустойчивой [*]• Фазовая скорость третьей ветви желобковых колебаний близка к угловой скорости дрейфа ионов
недостаточно полно. Дело в том, что в реальных системах скорость дрейфа ионов зависит от радиуса. Поэтому, вообще говоря, нельзя исключить возможности совпадения, при каком-то значении радиуса, фазовой скорости колебаний и скорости дрейфа ионов. При этом становится возможным резонансный обмен энергией между колебаниями и плазмой, который, как мы увидим ниже, будет приводить к затуханию колебаний. Поскольку декремент затухания не зависит от вида функции распределения ионов по скоростям, а всецело определяется макроскопическими характеристиками плазмы (градиентом плотности, градиентом магнитного поля и т. д.), в работе [4] такие резонансы были названы гидродинамическими *.
По нашему мнению, именно этот эффект проявлялся в экспериментах [“• т], в которых была сделана попытка возбудить желобковые колебания при плотности ниже критической. При этом наблюдалась лишь электронная ветвь колебаний, остальные ветви оказались сильно затухающими. Мы считаем, что затухание обусловлено резонансным взаимодействием с дрейфовым движением ионов. В данной работе показано, что при той неоднородности магнитного поля, которая имела место в указанных экспериментах (скорость дрейфа на радиусе менялась в 1,5 раза), ионная и вармовская ветви желобковых колебаний должны быть затухающими. Нами получены зависимости декремента затухания от плотности плазмы и поперечной энергии ионов для различных профилей плотности плазмы.
Следует отметить, что вармовская ветвь желобковых колебаний в настоящее время привлекает к себе пристальное внимание. Дело в том, что ее возбуждение должно приводить к очень быстрому выбросу плазмы на стенку камеры. Действительно, поскольку фазовая скорость вармовской ветви колебаний близка к скорости дрейфа ионов, то смещения ионов в таких колебаниях будут весьма велики даже при малой амплитуде колебаний. В последнее время появился ряд работ, в которых учитывается влияние различных факторов на устойчивость этой ветви колебаний. Так, например, в [3] показано, что к неустойчивости может привести наличие двух максимумов на функции распределения ионов по энергиям. Причем эта неустойчивость может развиваться как в ловушках с простым пробочным полем, так и при наличии минимума В. В [*] найдено, что причиной неустойчивости может являться градиент ионной температуры. Фазовая скорость вармовской ветви желобковых колебаний (1) близка в скорости дрейфа ионов
Со а
------- СОо^СОо —.
Т Я
Тот же порядок величины имеет изменение скорости дрейфа ионов по радиусу Лсовв(1)#(а)—а)в(0)«а^соо/йг«а)оа/Д. В силу этого весьма вероятно совпадение при каком-то значении радиуса фазовой скорости колебаний и скорости дрейфа ионов. Мы покажем, что резоцанс действительно осуществляется практически при любой неоднородности магнитного поля и приводит к затуханию колебаний в широком диапазоне значений плотности.
Для определения спектра частот желобковых колебаний необходимо решать дифференциальное уравнение, описывающее их пространственную структуру. При совпадении фазовой скорости колебаний и скорости дрейфа ионов в этом уравнении появляется сингулярность (особая точка соответствует точке резонанса). Особенность можно устранить, если учесть
Разброс в значениях энергии ионов, который всегда существует в реальной плазме. При этом дифференциальное уравнение настолько усложняется, что может быть решено лишь численными методами.
1. Резонансное поглощение
Используя сначала простейшую модель, мы покажем на примере ионной ветви, что резонансное взаимодействие может действительно приводить к затуханию колебаний. Рассмотрим цилиндр плазмы с плотностью, слабо меняющейся во внутренней области и резко обрывающейся у края плазмы. Предположим, что магнитное поле направлено вдоль оси цилиндра (ось ог). В такой системе желобковые колебания представляют собой волны электрического потенциала и плотности бегущие по азимуту 0 и не зависящие от 2, /~/(г)е“<"*'Ит0. Радиальная зависимость возмущений определяется уравнением
|
1 11 С^ф! Ш2 |
|
Ф| + —( <В< |
|
) |
|
Г (1гГ (1г г2 |
|
0)< 0) 0)—ЛЪ(й0 (г) / г дт |
|
|
|
Здесь о)р1 — плазменная ионная частота, <р4 — возмущение электрического потенциала. Уравнение (2) можно получить, считая, что заряженные ча-
|
А также используя уравнения неразрывности для электронов и ионов и уравнение Пуассона (например, [*]).
Пренебрежем сначала слабым изменением плотности во внутренней области плазмы, т. е. будем считать, что зависимость плотности от радиуса имеет вид
(г>а).
Предполагая также для простоты, что металлический кожух, который обычно окружает плазму, отсутствует, получаем
|
|
|
![]()
![]()
|
Вием гй1 = - 7 |
![]()
|
•г |
![]() На рис. 1 изображена зависимость частоты колебаний от плотности плазмы для ловушек с простым пробочным полем, в которых ®0ве/то|©г гН-<Ш/с1г<0. Верхняя ионная ветвь с а)>(72)о)0(а) соответствует знаку «плюс» в (3), нижняя электронная с а)<(|/а)со0(а) — знаку «минус». Из
На рис. 1 изображена зависимость частоты колебаний от плотности плазмы для ловушек с простым пробочным полем, в которых ®0ве/то|©г гН-<Ш/с1г<0. Верхняя ионная ветвь с а)>(72)о)0(а) соответствует знаку «плюс» в (3), нижняя электронная с а)<(|/а)со0(а) — знаку «минус». Из
(3) Следует, что при плотности выше критической, определяемой усло-
Обе ветви сливаются и колебания становятся
Неустойчивыми.
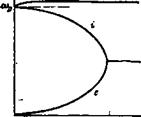
На рис. 2 приведена зависимость скорости дрейфа от радиуса. Из рисунка следует, что при достаточно низких значениях плотности, когда частота ионных колебаний не слишком отличается от со0(а) должно выполняться равенство: со/т=©0(г,), где 0<г,<а.
Учтем теперь, что в области г<а градиент плотности плазмы хотя и мал, но отличен от нуля. Для вычисления поправки к частоте собственных колебаний используем метод последовательных приближений. Помно-
|
|
|
Рис. 2. Характерная зависимость угловой скорости дрейфа и плотности плазмы от радиуса. В точке г, фазовая скорость колебаний со/т равна скорости дрейфа ионов |
Жим (2) на ф/(г) и проинтегрируем по частям. При наличии резонансной точки определим 1/(©—тосо0(г)) как р/(©—т©0(г)) — £лб(©—т<й0(г)).
В результате для мнимой части частоты получим следующее выражение:
1шш-------- ?—(------------- 1--------------- - Ц"х
©р<а(а) (о)-тсо0(а))2 а)2/ //ч
(4)
Таким образом мы показали, что резонансное взаимодействие с дрейфовым движением ионов может приводить к затуханию ионной ветви же - лобковых колебаний (ср. с [9]).
В принятой нами упрощенной модели все ионы, расположенные на данном радиусе, характеризуются одним и тем же значением скорости дрейфа, что соответствует моноэнергетическому распределению ионов. В реальных системах распределение ионов по энергиям обладает некоторым разбросом. Это обстоятельство приводит к размытию области резонансного взаимодействия и соответственно к устранению особенности в дифференциальном уравнении, описывающем радиальную зависимость желоб - ковых колебаний. Чтобы учесть эти эффекты, необходимо кинетическое рассмотрение, что и будет сделано в следующем разделе.
2. Основное уравнение
Движение ионов в поле желобковых колебаний будем описывать кинетическим уравнением
<?/. 91, е д/, е д/о,
----- + V-------- 1------- [уН]---------------- V©!----- — О. (5)
ДЬ дт тпіС д ду
Здесь /і — возмущение функции распределения ионов, /о — начальная невозмущенная функция распределения ионов. Начальная функция распре-
Деления ионов по скоростям является функцией интегралов движения на невозмущенных траекториях:
Т{иг. , и9
8-------- Г-. т1='д+г —.
2 Со *
Где — азимутальная компонента скорости ионов. Зависимость функция распределения ионов по скоростям от т) и е выбиралась в следующем виде:
/о5“(Ло(Т|)/ДєЯІ/і) ехр (— (е—e0)7(Ae)a), (6)
Где Де — дисперсия ионов по поперечной энергии.
Применяя стандартную процедуру интегрирования по траекториям (например, [9]), из уравнения (5) можно получить возмущение плотности ионов:
Ј(-B&r*
TOC O "1-5" H Z X ГіУл + — (1+ПГя*ДГ(*,))1 . (7)
L dr Де с J
Здесь (2«Дв1.-^-) +-^, +
О
Интеграл вероятности комплексного аргумента. Последнее слагаемое в правой части выражения (7) учитывает эффекты, связанные с возмущением скорости дрейфа ионов о)0 в неоднородном магнитном поле.
Чтобы получить возмущение плотности электронов п1ву воспользуемся уравнением неразрывности и учтем, что электроны дрейфуют в возмуще-
С
Ниях потенциала со скоростью vle = —[НУф]. В результате получаем
2ефі т dn0
р)
Ів CD771,0)і d (г1)
Подставляя (7) и (8) в уравнение Пуассона, находим 1 d гіфі 77i2 ^ 2т dcopi2
Тг 2т dtopi1 т{ /1 dH -1
Т'4’* ww7 <f(г1) Ч’,-ф‘дГІІГ ^г1) ) х
Г dr dr
Для дальнейших вычислений удобно ввести безразмерные переменные / Г 2 е, _ 0)
*-(т)- г-1Г - "“мог
А =
В этих переменных уравнение (9) будет выглядеть следующим образом:
<22г|? г тг—1 А 1 с1п0
|
Х (1+2р/ах) і По >(*) ‘.(0) |
|
(іхг I 4а:2 іах п0 (ЇХ А (1—ах—рх2)гг 1 <1пй — |
![]()
|
т--- ^гу„^(2>.) + I. п0 ах |
![]() Ч
Ч
+ 27чй)-^^-а(1+«Уяг(^(г()) Н=0. (10)
|
Здесь |
![]() Ло(0) Л
Ло(0) Л
Я (х) =Я,(1-ах-рх2); А = —^л, .
2а)<а)о(0)
Будем считать, что на границе плазмы, т. е. при г—а (х=1), расположена металлическая стенка, на которой возмущение потенциала ф! обращается в нуль. Поэтому граничные условия для уравнения (10) примем в виде
Ф(0) =Ж=Ч>(1) =0.
3. Численные расчеты
А. Общая схема
Уравнение (10) решалось численно методом Рунге — Кутта с автоматическим выбором шага [10]. Чтобы начать счет из точки х=0, решение
*
У(х) в окрестности х=0 находилось в виде ряда по х: фрс)ж ^ Слхп+Л.
|
|
|
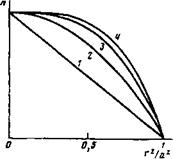
Рис. 3. Профили плотности плазмы, для которых проводились численные расчеты по (г) »По (0) (1—(г/а)2*). Кривые 1, 2, 3, 4 соответствуют значениям к—1, 2, 3, 4 |
Интегрируя численно уравнение (10), мы находили значение яр на стенке ж—«1, Чтобы определить частоту колебаний Ие© и декремент затухания 1та, необходимо было решить систему уравнений
Иеф(1, Яво, 1шо)«0,
(11)
1тф(1, Ие©, 1т© «0.
Система уравнений (11) решалась методом Ньютона [1в], причем для получения корней с точностью 10"а требовались лишь одна-две иттера-
Ции. Следует отметить, что интеграл вероятности W(z} при — Зя/4< <arg z< —я/4 экспоненциально растет с ростом |z<|, и поэтому численные расчеты практически возможны лишь при не слишком больших декрементах затухания. Расчеты проводились для различных профилей плотности плазмы, причем зависимость плотности от радиуса выбиралась в виде
Ло=М0) (1 ят*) - Ио(О) (1 -(г/аП,
Где &=1, 2, 3, 4. Кривые л0(х) для различных к изображены на рис. 3. Для магнитного поля принималось выражение Н(х)=Н(0) (1—ах—(to2), а*в0,142; (}=0,009, что соответствует условиям экспериментов [в-7]. Численные расчеты проводились для первой моды (/71=1) ионной и вар - мовской ветвей желобковых колебаний. Сначала мы обсудим результаты расчетов ионной ветви.
Б. Ионная ветвь желобковых колебаний
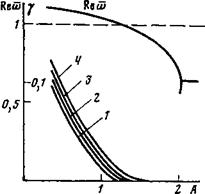 На рис. 4, 5 показаны зависимости частоты и декремента затухания ионной ветви колебаний от плотности плазмы. Различные кривые на рис. 4 соответствуют различным профилям плотности плазмы. Так как частота колебаний нормирована на со0, (0), то при уменьшении плотности* когда © оказывается равной единице, в плазме появляется резонансная точка. При этом, как видно из рис. 4, 5, колебания становятся затухаю*
На рис. 4, 5 показаны зависимости частоты и декремента затухания ионной ветви колебаний от плотности плазмы. Различные кривые на рис. 4 соответствуют различным профилям плотности плазмы. Так как частота колебаний нормирована на со0, (0), то при уменьшении плотности* когда © оказывается равной единице, в плазме появляется резонансная точка. При этом, как видно из рис. 4, 5, колебания становятся затухаю*
|
|
Рпс. 4 Рпс. 5
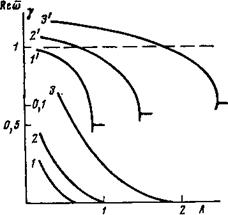
Рис. 4. Зависимость частоты колебаний Песо (кривые помечены штрихами) и декремента затухания ионной ветви от плотности плазмы при Т=30. Раз
Личные кривые соответствуют различным профилям плотности плазмы. 1 - »оИ-МО) (1-(г/а)*), 2 — По (г) =*по(0) (1- (г/а)4), 3-п0(г)=п0( 0) (1 - (г/а)8)
Рис. 5. То же, что и на рис. 4 при п0(г)=л0(0) (1— (г/а)9). Различные кривые для декремента колебаний V соответствуют разным значениям Т, кривая 1— 2,1*в35,
2 - Г2-30, 3 - Гз-25. 4 - Т^20
Щими. Х^еличение критической плотности при укручении профиля плотности плазмы объясняется стабилизирующим влиянием проводящей стенки. Действительно, поскольку мы считаем, что стенка расположена на границе плазмы (г=а), То укручение профиля плотности плазмы приближает область максимального градиента к стенке.
Отметим, что для всех профилей плотности, для которых проводились расчеты, получилась одинаковая качественная картина поведения декремента затухания колебаний.
На рис. 6 показана зависимость величины декремента от дисперсии ионов по поперечной энергии Т для плотности плазмы, соответствующей А =0,6. Как видно из рис. 6, декремент затухания колебаний довольно слабо меняется при изменении Т. Этот результат соответствует теории гидродинамического резонансного взаимодействия, согласно которой эффект резонансного взаимодействия не должен зависеть от вида функции распределения.
В. Вармовская ветвь желобковых колебаний

|
0^07 0}0В 0.05 |
![]()
|
15 |
![]()
|
20 25 30 Т~сд! Ас |
![]()
|
Рис. 6 |
![]() Обсудим теперь результаты расчетов вармовской ветви желобковых колебаний, которые представлены на рис. 7—9. На рис. 7 показана зависимость декремента колебаний у и частоты колебаний Ие ш от величины неоднородности магнитного поля по радиусу. Величина неоднородности
Обсудим теперь результаты расчетов вармовской ветви желобковых колебаний, которые представлены на рис. 7—9. На рис. 7 показана зависимость декремента колебаний у и частоты колебаний Ие ш от величины неоднородности магнитного поля по радиусу. Величина неоднородности
|
|
|
Рис. 7 Ионов по |
|
Поперечной |
Рис. 6. Зависимость декремента затухания ч от дисперсии
Энергии Г=ео/Де
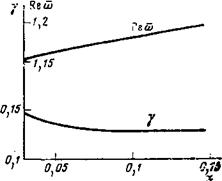
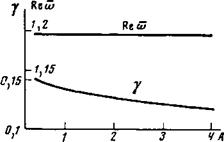 Рис. 7. Зависимость частоты колебаний Песо и декремента затухания '*=—1т (5 вармовской ветви от неоднородности магнитного поля #=#(0) (1—ах—рх2). При расчетах мы полагали £=0,46 а2, Т=10, А—2
Рис. 7. Зависимость частоты колебаний Песо и декремента затухания '*=—1т (5 вармовской ветви от неоднородности магнитного поля #=#(0) (1—ах—рх2). При расчетах мы полагали £=0,46 а2, Т=10, А—2
|
|
Рпс. 8 Рис. 9
Рпс. 8. Зависимость частоты п декремента затухания вармовской ветвп от плотности плазмы Л~по(0), Г* 10, а=0,142 Рис. 9. Зависимость частоты и декремента затухания вармовской ветви от дисперсии ионов по поперечной энергии Т=*ъо/Де, А—2
Магнитного поля характеризуется параметрами а и Ц, которые при расчетах изменялись одновременно. Причем мы считали, что (}~а Кривые на. рис. 7 сосчитаны для 10 и А=2. Как и следовало ожидать, частота колебаний спадает с уменьшением неоднородности магнитного поля. Слабая зависимость декремента колебаний от неоднородности магнитного поля связана с тем, что резонансная точка существует в плазме даже при достаточно малых значениях а. Возрастание декремента при уменьшении неоднородности магнитного поля объясняется увеличением размера резонансной области Дх,~1/аТ. Отметим, что результаты расчетов остаются справедливыми и для параболического распределения магнитного поля Я=#(0) (1—а(г/а)2), р*«0, так как роль коэффициента Р сводится лишь к эффективному увеличению неоднородности магнитного поля.
На рис. 8 показана зависимость частоты и декремента затухания вармовской ветви от плотности плазмы в центре ловушки (величина А, отложенная по оси абсцисс, пропорциональна плотности плазмы). Напомним, что порогу неустойчивости желобковых колебаний по плотности (га^аЯ) [*] соответствует значение А~1.
Наконец, на рис. 9 изображена зависимость частоты колебаний и декремента затухания от дисперсии ионов по поперечной энергии. При больших значениях во/Де (при малой дисперсии) величина декремента затухания приближается к гидродинамическому декременту затухания, который соответствует Де**0. С уменьшением Т (с ростом дисперсии ионов по поперечным энергиям) размер резонансной зоны увеличивается и декремент затухания возрастает. Как видно из рис. 9, частота колебаний практически не зависит от Т.
Таким образом, как показывают результаты расчетов, последовательный учет неоднородности приводит к тому, что вармовская ветвь колебаний становится устойчивой. Мы рассматривали затухание третьей ветви без учета дестабилизирующих факторов, например, таких, как градиент температуры [•]. В нашем случае роль температуры играет средняя энергия ионов вв. Однако и при наличии градиента температуры необходимо учитывать затухание вармовской ветви из-за резонансного взаимодействия с ионами. Оценки показывают, что учет резонансного затухания в наших условиях приводит к пороговому значению градиента температуры (средней энергии), которое в 2—3 раза превышает полученное в [•].
Таким образом, как показывают результаты расчетов, последовательный учет неоднородности магнитного поля приводит к тому, что обе рассмотренные ветви колебаний становятся затухающими. В отличие от ионной ветви, которая затухает лишь при низкой плотности плазмы, реознансное поглощение вармовской ветви желобковых колебаний происходит в достаточно широком диапазоне изменения плотности плазмы.
Эффект резонансного затухания, по-видимому, препятствовал возбуждению ионной и вармовской ветвей желобковых колебаний в экспериментах Йт]. Следует отметить, что при наличии достаточно большого разброса ионов по энергиям желобковые колебания будут затухать, даже если скорость дрейфа постоянна по радиусу. В этом случае с колебаниями взаимодействует некоторая группа ионов из распределения ионов по скоростям, и резонансное взаимодействие осуществляется во всем пространстве (гидродинамический резонанс переходит в кинетический). Оценки показывают, что такой переход осуществляется при Де/е>Дсйо/сйо. Однако в условиях экспериментов [в’т] выполняется обратное неравенство, и, следова-
Тельно, гидродинамическое резонансное взаимодействие преобладает над кинетическим. За обсуждение работы авторы благодарны В. А. Чуянову.
Институт атомной энергии
533.95