ФИЗИКА ПЛАЗМЫ

В ы п. 4 УДК 533.9.082.74 РЕЗОНАНСНЫЕ ЭФФЕКТЫ И НЕУСТОЙЧИВОСТЬ ПУАЗЕЙЛЕВСКОГО ТЕЧЕНИЯ

ТИМОФЕЕВ А. В.

1. В теории плазмы отчетливо прослеживается тенденция к выявле­нию закономерностей, позволяющих с единых позиций рассматривать ко­лебания произвольных сплошных сред (плазма, газ, жидкость, .гравити - рующая среда) [1—7]. Этой цели служит и настоящая работа, в которой механизм неустойчивости, действующий в течениях обычной жидкости с профилем скорости без точек перегиба (пуазейлевское течение, течение в пограничном слое), связывается с резонансным взаимодействием меж­ду колебаниями и движением жидкости. Отметим, что на одной из ветвей плазменных колебаний обнаружена неустойчивость, вполне аналогичная неустойчивости пуазейлевского течения [8—10]. Возможно, что четкое представление о механизме таких неустойчивостей позволит выявить и другие аналоги.

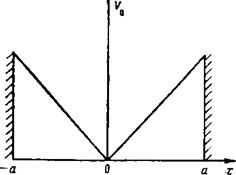
2. В [11] отмечено, что при выяснении физических закономерностей, определяющих устойчивость неоднородных течений, удобно рассматри­вать течения, профиль скорости которых имеет излом. Точке излома соот­ветствует слой жидкости, создающий коллективную степень свободы. Следуя [11], заменим плавный пуазейлевский профиль скорости профи­лем, изображенным на рис. 1. Он приведен в системе отсчета, где слой жидкости, поддерживающий колебания, покоится. В этой системе стенки, ограничивающие поток, движутся вверх по течению со скоростью У0(а).

Уравнение Орра — Зоммерфельда, описывающее колебания плоско - нараллельного течения несжимаемой жидкости, представим в виде

Здесь <р=<р(х)ехр(—I©T+Iky) — возмущение функции тока. Vn=V0{X) — Певозмущенная скорость течения, направленная по оси 0У, v — кинема­тический коэффициент вязкости, А=(дг/дхг)—кг, ось ОХ направлена по­перек течения, ось 0У — вдоль.

Если, считая вязкость малой, пренебречь правой частью уравнения (1), то оно примет вид уравнения Шредингера с узкой потенциальной ямой. Его решение, удовлетворяющее граничным условиям <р(±а)=0, имеет вид <p=sh(fc(a— х). Частота соответствующих собственных коле­баний равна (й=1/2АУо' ih Ка, где Л V/ — скачок производной У0(я) в точке г=0.

Вязкость жидкости необходимо учитывать вблизи границы, а также при V0'(X,)^Q в окрестности резонансной точки Xty определяемой равен­ством (A/K=Vо(х,). Действие вязкости приводит к обращению в нуль на границе тангенциальной компоненты скорости Vyl=Dq>/Dx. В погранич­ной области наряду с медленно меняющимся «идеальным» решением уравнения (1) (см. выше) необходимо учесть и «вязкое» — быстро спа-

Чающее от границы (характерный масштаб спада Дх —

F’2j. Чтобы учесть влияние вязкости, умножим (1) на ср* и проинтегри-

Й8'.

Руем по частям, учитывая быстрое спадание «вязкого» решения от гра­ницы. При этом для поправки к частоте собственных колебаний, обуслов­ленной действием вязкости, получаем следующее выражение:

TOC o "1-5" h z Д Т * / | ®

Бш=-‘----------- 1П? Т~-------- тг~1Ь2(А:в)— Г <2х|Д<р|2. (2)

(О—ку0(а) к 4

а—Дх,

Здесь и считается также, что резонансная точка, если такая

Имеется, расположена вне «вязкого» пограничного слоя. Интеграл, вхо­дящий и (2), по порядку величины равен К2/Ах.

И;» (2) следует, что вязкость в пограничном слое действует на коле - бания жидкости точно так же, как кулоновские соударения на плазмен-

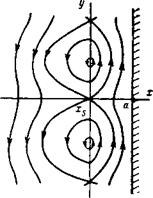
Рис. 1. Простейший профиль скоро - Рис. 2. Линии тока в окрестности ре -

Сти с изломом, эквивалентный про - зонансной точки при возмущении ко -

Филю скорости пуазейлевского те - нечной амплитуды

Чения

Ные колебания при наличии частиц, движущихся со скоростью, близкой к фазовой скорости волны. А именно, пристеночный слой; обгоняющий волну, отдает ей свою эцвргию, а отстающий отбирает энергию у волны. Влияние пристеночного слоя возрастает при <й/к-+У&(а). Именно такие колебания и неустойчивы в пуазейлевском течении и в течениях типа пограничного слоя [12].

3.Анализ, колебаний, резонирующих с течением в пристеночном «вяз­ком» сдое«, сопряжен с значительными математическими трудностями, преодолеваемыми обычно о. помощью ЭВМ. Чтобы наглядно представить себе процессы, действующие в окрестности-резонаясной -точки, полезно рассмотреть, возмущения конечной амплитуды. Перейдем в систему от­счета, движущуюся со скоростью V=(O/K, при этом в окрестности резо­нансной точки функция тока примет вид

Ф (г) = V0' (X,) (х-х.) 2 4- 4- Vo' (х.) (х-х.) 3+ ... +ср (х) Cos ку.

1 о

В силу соотношений У-х^-пдФ/ду, Vy—дФ/дх функция тока играет роль

Гамильтониана, а координаты х, У — роль гамильтоновых переменных — импульса и координаты соответственно. Эта аналогия позволяет легко представить характер движения жидкости на плоскости ХОУ. Так, если положить V0(^s) = ^o =0, <p(:r)=const, то картина линий тока

Примет такой же вид, какой имеет фазовая плоскость в случае заряжен­ных частиц, движущихся в поле волны конечной амплитуды. При V0"(X,)Ґ*0 картина движения становится асимметричной относительно линии X=Xf. Если, например, V"(Xt)>04 что соответствует реальному пуазейлевскому течению, то волна захватит большу-ю массу жидкости слева от точки Хл, т. е. в области, где V0(X)<To/K (см. рис. 2). В резуль тате жидкость получит от волны некоторое количество энергии направ­
ленного движения, что должно привести к затуханию колебаний. Однако соображения, основанные на анализе баланса энергии волны и захваты­ваемой жидкости, справедливы лишь для свободного течения. Если же оно ограннчено стенкой, то система перестает быть замкнутой. В системе отсчета, принятой на рис. 2, стенка оогоняет колебания. Поэтому каждый раз, когда «захваченные частицы» проходят поблизости от стенки, они под действием вязкости увлекаются ею. В результате осуществляется по­стоянная пакачка колебаний.

Если анализировать процесс раскачки в лабораторной системе коор­динат. то мы придем к заключению, что вязкость вызывает диссипацию энергии колебаний, и, следовательно, им в этой системе следует припи­сать отрицательную энергию.

Таким образом, в настоящей работе показано, что жидкость в присте­ночном слое взаимодействует с колебаниями течения так же, как резо­нансные частицы с колебаниями плазмы, а именно раскачивает колеба­нии, если пристеночный слой обгоняет их, и демпфирует колебания в обратном случае. Взаимодействие с пристеночным слоем и приводит к не­устойчивости пуазейлевского течения.