Уравнение Фоккера—Планка
Рассмотрим ансамбль ионов, взаимодействующих с плазмой дуги. Плазму дуги будем считать нейтрализованной. Потери энергии ионов определяются параметрами самой дуги, которые постоянны во времени, а также энергией ионов. Это обстоятельство позволяет описать процесс взаимодействия ионов с плазмой дуги при помощи одномерного уравнения Фоккера—Планка^]
TOC o "1-5" h z £-4-$-4-*(£)„= <?(£,<). (1)
Здесь п(Е, £) — функция распределения ионов по энергии в зависимости от времени
Поток ионов по шкале энергий (см[1]),
С1 (ЛЕ) 2Е (М л 2Е. ,ч Е
* (л£)2___ =^1 (л
СН х{/' I х )х, х{/»' х,' ‘ *
где
= Х‘=ЪЪ х' = Тг
О
Т„ Т{ — температура электронов и ионов дуги соответственно; = 1 / Л/ 1 Е3/1
= т|/< = т1= у ’ ^ — кулоновский логарифм; л0 — плотность
Плазмы в дуге.
Для „Огры“ имеем Е — 50 кэв, Тв ~ 10 эв, Е^> ТX = 11, л0 — 1013. При этом хв—1, х,^>1, а т« ^ ~ ^ V Поэтому в выражении для
Потока можно пренебречь вторым слагаемым, т. е. положить, что у =
TOC o "1-5" h z ЛЬЕ </Д£ . *
;=л-^-, причем для, отбрасывая малые более высокого порядка,,
Получаем
</(Д£) 2 ЕМ , . ...
Отброшенное нами второе слагаемое в выражении для потока учи* тывает тот факт, что даже при „далеких* кулоновских соударениях энергия изменяется не непрерывно, а скачками. Это обстоятельство приводит к „диффузии* ионов по шкале энергии. Не учитывая ее, мы тем самым уподобляем движение иона движению макроскопического* тела в вязкой жидкости.
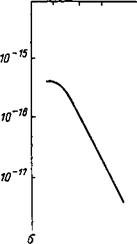
В. уравнение (1) добавлен член v(£)л, который учитывает потери ионов в результате перезарядки на нейтральных атомах у(£) =
= (£)/!„.; о (Е) = 2 • 10—14—»-••» СМ* (£>15 ка в) (рис. 1) —се-
Чение перезарядки водородных ионов на нейтральных атомах[2], п^-= = 10® см-3 — плотность нейтральных атомов. Мы считаем, что атомарные ионы возникают из молекулярных с.
 Кэ где функция f(t) постоянна во время импульса тока инжекции и равна нулю в промежутке между импульсами.
Кэ где функция f(t) постоянна во время импульса тока инжекции и равна нулю в промежутке между импульсами.
Выше мы предположили, что траектория иона целиком содержится в области, занятой электронной дугой. Однако обычно дуга занимает лишь небольшую часть объема, установки, вследствие чего лишь часть траектории иона проходит через дугу. Далее будет показано, что этот факт может быть учтен введением в выражение (5) множителя,, равного отношению времени пребывания иона в дуге к полному периоду времени между двумя последовательными прохождениями иона через дугу.