Основные уравнения
Мы рассматриваем плазму как двухкомпонентную жидкость, состоящую из электронов и ионов, которые при движении сталкиваются с нейтральными атомами. Эти столкновения учитываются в уравнениях
V,
Движения членом с трением------- — — среднее время между столкно-
Вениями). Если ограничиться медленными колебаниями с частотами много меньшими частоты соударений, то движение можно считать безынерционным. Тогда уравнение движения электронов принимает вид
|
|
|
Тпв |
|
Т |
(1)
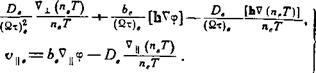
|
Мы приняли следующие обозначения: пв—плотность электронов; <р — потенциал ' электрического поля; Т—температура электронов; |
![]()
![]()
|
(2) |
![]() Откуда для скорости электронов получаем
Откуда для скорости электронов получаем
2# — электронная циклотронная частота; = —- — коэффициент диф-
Т
Фузии электронов; = ---- подвижность электронов; ух# — скорость
Электронов поперек магнитного поля; 1>1(#— скорость электронов вдоль магнитного поля; Ь — единичный вектор, направленный вдоль магнитного поля.
Обычно температура электронов больше ионной, так что ионы можно считать холодными.
В (2) величина магнитного поля предполагалась такой, что электронная циклотронная частота намного больше частоты соударений электронов с нейтралями. Предположим также, что для ионов выполняется обратное соотношение, т. е. (2т)#^> 1 и (2т)< 1. Тогда действием
Магнитного поля на ионы можно пренебречь. .При этих условиях для скорости ионов имеем
TOC o "1-5" h z у< = — б^ср. (3>
Поведение плазмы описываем уравнениями непрерывности для электронов и ионов и уравнением теплового баланса
V (л, т.) = 0; = (4)
-|-л,-^--4-л,7’<11ут,-*-сНуч=0. (5)
Для потока тепла q имеем из[2]
Здесь X•—коэффициент электронной теплопроводности. Колебания с частотой много меньшей электронной лэнгмюровской можно считать квазинейтральными и положить
Л*=Л. = Л. (7)
Подставляя в (4) и (5) выражения для скорости электронов (2) и ионов (3), а также для потока тепла (6), получаем систему уравнений для 7 л, <р.
Устойчивость колебаний исследуем, как обычно, при помощи линеаризованных уравнений для малых возмущений Ти пи срь зависимость которых от / и х в квазиклассическом приближении можно выбрать в виде е~{
В результате получаем следующую систему:
—/ш • -^--»-6. к2срх = 0,
Где со — частота рассматриваемых колебаний; &ц и к±— продольная и поперечная компоненты волнового вектора относительно магнитного поля.[1]