ФИЗИКА ПЛАЗМЫ

О СВЯЗИ ЦИКЛОТРОННОГО РЕЗОНАНСНОГО ВЗАИМОДЕЙСТВИЯ С ЧЕРЕНКОВСКИМ

ТИМОФЕЕВ А. В.

Введение

В динамике плазмы важную роль играет резонансное взаимодействие между заряженными частицами и плазменными колебаниями. Обмен энергией, сопровождающий резонансное взаимодействие, приводит к из­лучению или поглощению колебаний. При когерентном взаимодействии больших ансамблей частиц говорят о раскачке или затухании плазмен­ных колебаний. Известны два вида резонансного взаимодействия: черен - ковское и циклотронное. Принято считать, что черенковское резонансное взаимодействие происходит при равномерном движении заряженных ча­стиц, если их скорость удовлетворяет условию й)=ку, циклотронное — при вращении частиц во внешнем магнитном поле, если (й=п<йу Здесь ю,— циклотронная частота частиц сорта /=е, £, П — целое число. Может пока­заться, что циклотронное резонансное взаимодействие так же резко отли­чается от черенковского, как вращение от равномерного движения. Одна­ко на самом деле возможны условия, при которых различие между этими двумя видами резонансного взаимодействия стирается. Так, предположим, что частота колебаний существенно превышает циклотронную частоту за­ряженных частиц, а длина волны мала по сравнению с их ларморовским радиусом. Рассмотрим частицу, скорость которой, при вращении по цикло­тронной окружности в некоторый момент времени удовлетворяет условию черенковского резонанса й)=ку‘. Тогда в течение времени б£, много боль­шего периода колебаний 2л/ю, частица будет двигаться в фазе с волной, т. е. пребывать в состоянии резонанса. Резонансное взаимодействие пре­кратится из-за поворота вектора скорости в магнитном поле.

Поскольку данная ситуация представляет собой частный случай взаи­модействия в магнитном поле, то она, разумеется, может быть описана в терминах резонансного циклотронного взаимодействия. Однако описание существенно упрощается, если в качестве исходного пункта анализа счи­тать, что в данном случае мы имеем дело с резонансным черенковским взаимодействием при неравномерном движении заряженных частиц. Такое расширение понятия о резонансном черенковском взаимодействии в ряде случаев оказывается весьма полезным[68]. Так, например, оно позволяет по-новому взглянуть на роль ускорения при излучении электромагнитных волн релятивистскими частицами в вакууме. Как известно, скорость ча­стиц всегда меньше скорости света. Поэтому считается, что черенковское излучение в вакууме невозможно. Однако если выполняется условие с—17<с, то в течение времени 6£[69], когда вектор скорости частицы близок по направлению к волновому вектору колебаний, фаза последних на тра­ектории частицы будет меняться весьма медленно. Если 6£< (аз—ку)"1, то
можно говорить о состоянии фазового резонанса между частицей и коле­баниями. Действительно, в этом случае в силу «соотношения неопреде­ленности» Д£Дю^1 (Д(о=(о—ку) за время 6£<Д£ не успеет проявиться отличие скорости частицы от скорости света. В течение времени частица будет излучать «по Черенкову». Время уменьшается с увеличением ускорения, при этом допустимая условием «фазового резонанса» разность С—и возрастает. С этих позиций удается сравнительно просто интерпре­тировать основные свойства синхротронного излучения (см. [3, 4], а так­же Приложение 1), которые обычно получаются как результат громозд­ких расчетов.

Цель настоящей работы — анализ черенковского резонансного взаимо­действия заряженных частиц, движущихся во внешнем магнитном поле* В работе установлены условия, позволяющие при анализе взаимодействия ансамбля заряженных частиц с колебаниями пренебречь влиянием маг­нитного поля.

1. Резонансное взаимодействие в слабом магнитном поле

Колебательные свойства плазмы полностью описываются тензором ди­электрической проницаемости е,„ поэтому все утверждения относительно характера взаимодействия частиц плазмы с колебаниями должны найти: свое отражение в свойствах этого тензора. С интересующей нас точки зрения отдельные компоненты тензора еу несущественно отличаются друг от друга. Чтобы уменьшить число формул, ограничимся потенциальными колебаниями, которые характеризуются одной скалярной величиной е= =Ъцкук}1кг. Для определенности будем рассматривать резонансное взаи­модействие ионной компоненты плазмы с колебаниями и соответственно анализировать ионную часть скалярной диэлектрической проницаемости:

(і)

Где й)р< — плазменная ионная частота, /„ — функция распределения ионов, /п — функция Бесселя, р< — ионный ларморовский радиус. Чтобы исклю­чить влияние эффекта Доплера, вызванного равномерным движением ионов вдоль магнитного поля, который не имеет отношения к интересую­щей нас проблеме, рассмотрим колебания, распространяющиеся поперек магнитного поля (вдоль ОХ) ~ехр(—

Координата иона Х меняется по закону я(£) ^^о+рДэт 0(*) — этбо), где 0(0 =0о+й)^ — фаза ларморовского вращения. В соответствии с из­вестной формулой

Исходная плоская волна может быть разложена по цилиндрическим, вра­щающимся коаксиально с любым из ионов

Где $=к(х9—Р^тбо^сопэ^ Поскольку в=о><, то при выполнении усло­вия циклотронного резонанса й)=гсй)< фаза П-й цилиндрической гармони­ки постоянна на траектории иона. Это свидетельствует о резонансе между данной парциальной составляющей плоской волны и ионом. Множитель Л»2(&Рг) в (1) дает вес резонансной цилиндрической гармоники в исход­ной плоской волне.

Изменение энергии колебаний в результате резонансного взаимодейст­вия с ионами определяется выражением

TOC o "1-5" h z \г=-со 1те(,)/с2|ср|74л, (2)

Где ф — возмущение электрического потенциала.

1 Р

Используя соотношение ---------------------- — Іл6((і) — П(0і), Из (1)

(О—П(0{ 0) — П(0і

Получаем

ОО ОО

1те(,)=—2л*(~т“) ^ Па>і6(а>—П(й{) | /Я2(&Р<)- (3)

К ' (IV

Л— — ОО о

Из (2), (3) следует, что колебания обмениваются энергией с ионами при выполнении условия циклотронного резонанса й)=7Ш<. Используем выражение (3) для того, чтобы установить условия перехода циклотрон­ного резонансного взаимодействия в черенковское. Поскольку черепков­ский резонанс характерен для незамагниченной плазмы, то устремим ве­личину магнитного поля к нулю. В пределе ю.--*0 дискретный спектр пе-

ОО оо

Реходит в непрерывный и соответственно сумма — в интеграл | Йп.

П—— ОО —со

Благодаря наличию 6-функции б (со—ло)<) последний легко вычисляется:

В»

1тв<*>—2л(-^ )*-£. (*Р<). (4)

Переход к приближению непрерывного спектра был совершен нами формально. В Приложении 2 показано, что это приближение законно, если «фазовая память» иона ограничена временем т<<ог1. Время т может оп­ределяться такими факторами, как столкновения (т=у-1, V — частота столкновений), уширение линий колебаний (т =(Лй))-1, До) — ширина ли­нии), рост амплитуды колебаний по времени (т=,у"1, ^ — инкремент ко­лебаний). Наконец, если амплитуда электрического поля колебаний доста­точно велика, то само движение ионов может стать стохастическим [2, 5], что естественно приведет к ограничению т.

Отметим, что наряду с эффектом ограниченности «фазовой памяти» к уширению циклотронных резонансов могут приводить не учитываемые нами эффект Доплера (при 0) и релятивистская зависимость цик­лотронной частоты от энергии. Если функция распределения заряженных частиц по скоростям в достаточной степени размыта (см. ниже), то спектр резонансного взаимодействия может стать непрерывным даже при т=°°.

Будем считать магнитное поле достаточно слабым, так чтобы выполня­лись условия й)>й)<, Кр{=ки±/(й^.

При /гр<>(о/(1)<> 1 асимптотическое представление функции Бесселя имеет вид (см., например, [6])

)'(№,)■ -1)-см(^(тга(^) -

Х леи 7 х (О 7 7 '(!)< х х Ки± 7

(5)

Подставляя (5) в (4) и усредняя по быстрым осцилляциям подынтеграль­ного выражения, т. е. заменяя соз2(...) на V*, находим

(*)■ - г

В качестве нижнего предела интегрирования мы взяли значение і;хвй)/Л,

Поскольку при V±<To/K выражение (6) становится мнимым (е(|) — дейст­вительно), что говорит о невозможности резонансного взаимодействия в области И±<(й/к. Отметим однако, что при И±<(й/к (icp<=A:i;x/(i)i<o)/(i)<) асимптотическое представление (5) неприменимо, поэтому ограничение области интегрирования значением Ю/к может показаться недостаточно обоснованным. Этот вопрос будет разъяснен ниже в разд. 3, где детально анализируется резонансное взаимодействие при И±^ы/к.

В выражение (6) не входит магнитное поле, поэтому оно может быть получено более просто, если с самого начала не учитывать действия маг­нитного поля на ионы. В приближении незамагниченных ионов выраже­ние для скалярной диэлектрической проницаемости, как хорошо извест­но, имеет вид

Im е(1>=— ) X

X J б((о—kv). (7)

Хотя слабое магнитное поле не влияет на волновые свойства плазмы, оно ска­зывается на виде функции распределе­ния. В магнитном поле стационарная функция распределения не может зави­сеть от Vx и Vv по отдельности, но лишь от комбинации V±=(Vx2+Vv1)L,T. Именно такая зависимость принималась выше в (1).

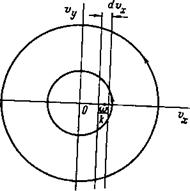
Перейдем в (7) от декартовых коор - Рис. 1. Траектории ионов в фазовой динат к полярным 0). Наличие в пространстве

(7) б-функции б (со—Kv± cos 0) позволя­ет проинтегрировать по DQ. Результат интегрирования, как нетрудно ви­деть, совпадает с (6).

Ввиду того, что (7) описывает резонансное черенковское взаимодейст­вие ионов с колебаниями, появляется возможность наглядного истолкова­ния характерных особенностей выражения (6). Так, поскольку V±= = (Vx2+Vv2)'Ll>Vx, а условие черепковского резонанса имеет вид (й/к=их, то в резонансном взаимодействии участвуют лишь ионы с V^M/K (см. нижний предел интегрирования в (6)).

Число ионов со скоростью ух, лежащей в интервале (To/K) — (DvJ2)< <^х< (Tiilk) + (DvJ2) 1 пропорционально времени, в течение которого ско­рость отдельного иона меняется в данных пределах: Л=(2л/(о<) (и±г—

— (<й/к)г)~‘'^их. Это обстоятельство учтено в (6) весовым множителем ((KujcО)2—l)~v Оно наглядно иллюстрируется рис. 1.

Отметим, что (7) описывает резонансное взаимодействие ансамбля ионов, движущихся равномерно, в то время как в магнитном поле они вращаются по циклотронным окружностям. Возможность использования

(7) в этом случае будет обоснована в следующем разделе.

В заключение этого раздела приведем явный вид величины W — изме­нения энергии колебаний в результате резонансного взаимодействия с ионами. Подставляя (6) в (2), получаем

W------- - l) • (8)

Ш/к

Из (8) следует, что если у функции распределения ионов по И± имеется участок с Df0/Du±>0, то колебания могут оказаться неустойчивыми (W> >0). Поскольку /о-**0 при то в области достаточно больших зна­

Чений И± должно выполняться условие Dfo/Dv±<0. Поэтому неустойчи­вость замагниченной плазмы может возникнуть лишь как следствие раз­ностного эффекта, обусловленного уменьшением интенсивности резонанс­ного взаимодействия с увеличением И± (см. фактор ((ки±[(й)г—1)~ч* под интегралом (8)).

3 Физика плазмы, вьш. 2 193

2. Черенковское резонансное взаимодействие при ларморовском вращении

Покажем, что то же самое выражение (8) для W можно получить, не­посредственно проанализировав процесс обмена энергией между колеба­ниями и ионами, вращающимися по ларморовским окружностям. Исполь­зуя уравнение движения, получаем соотношение

W=—E(vV)(p(Ј, г).

Здесь W=Mu2L2 — энергия иона, <р(£, г) =фе"гЪ*+гкг. На траектории иона фаза рассматриваемых колебаний дается выражением

Ф (£) =—сOt+kx(t) =—(ot+kpi sin(cDiH-0o) +const. (9)

Учитывая (9), изменение энергии иона за один оборот по циклотронной, окружности A W представим в виде

/и) = — ец) ФDt +ш)Ехр(£Ф(0). (10)

При co/cDi^l, /фг>1 подынтегральная функция в (10) быстро осцил­лирует. Осцилляции прекращаются в окрестности точек стационарной фазы Ts, в которых выполняется условие черенковского резонанса D<S)/Dt= =—(O+Kux(Ts)=0. Эти области определяют значение интеграла (10). На каждый оборот по циклотронной окружности приходится две точки ста­ционарной фазы (см. рис. 1). При со/о)г> (Арг)'/2 слагаемое с полной про­изводной дает малый вклад в Aw. Опуская его, приводим (10) к виду

Aw=E(Ocf) (2N/Kax(T8A))'12 ехр(гфза), (11).

A—1,2

Где Ax(Tsa)=—(I>IV±SiTi((I>It8A+Q0)=±(I)I(V±2— (ca/A:)2)1/2 — ^-компонента уско­рения иона в точке стационарной фазы, exp(Ј<Dsa) — несущественный фа­зовый множитель. Изменение энергии иона, даваемое выражением (11) г можно интерпретировать как результат ускорения электрическим полем колебаний в течение времени 8£«|Ф|^* ~ (Kv±(Di)~'H. Действительно, из

S

(9) следует, что именно это время ион пребывает в состоянии резонанса с колебаниями (|Ф(£)—Ф(£3) |<1). К выходу из резонанса приводит по­ворот вектора скорости в магнитном поле.

Предположим, что время т, характеризующее «фазовую память» иона, много меньше интервала Ts2—Tsi. В этом случае приращения энергии в точках TSa нескоррелированы, и за один циклотронный период диспер­сия в значениях энергии возрастает на

AS5=4я(со/сог) (е<р)2({Kvjdd)2—1)“'/2.

Используя соотношение A2D=2DAt, где D — коэффициент диффузии по* энергии, получаем [2]

D=(O (еф)2 ({Kvj(>>)2—1) “,/а.

Поток ионов по оси энергии, очевидно, равен Jw=—(D/Mv±) (Df0/Du±). В силу закона сохранения энергии изменение энергии колебаний в ре­зультате взаимодействия с ионами равно W=— J DJw. Нетрудно видеть,

Что оно совпадает с выражением (8), полученным в приближении неза - магниченных ионов.

Заметим, однако, что этот вывод справедлив лишь, если не учитывать вклад в W ионов, поперечная скорость которых близка к фазовой скоро­сти колебаний (l>_l~cdM0 . Действительно, при V±-+Coik точки стационар­ной фазы, в которых выполняется условие сO/K=Vx1 сближаются (см. рис. 1), и как бы ни была коротка «фазовая память» иона, условие |Јsi— —Јs2|>t в конце концов будет нарушено. Резонансное взаимодействие в области скоростей V±~W/K анализируется в следующем разделе.

3. Эффект конечности времени резонансного взаимодействия (ЭКВРВ)

Выражение (4) описывает резонансное взаимодействие колебаний С ионами во всем интервале изменения у±(0<1;_|_<«>). В области значений V±~(D/K, где порядок функции Бесселя Ло/^ (&Рг) примерно равен ее ар­гументу, воспользуемся асимптотическим представлением (см., напри­мер, [6])

Ло/а, { (Kpi) ~ (2со/со<)'/з Ai (ri), (12)

Где Ai — функция Эйри аргумента т}= (со—Kv±) (сОг2со/2)~1/з. При Ки±>со оно сводится к (5), если в последнем положить Ки±~(д. В обратном случае (Kv±<Со) из (12) получаем

/о/со. (*Рг) ~2~и((дг/(л(д))72 (1— (Ки±/(0)) ~'и ехр ( (2/з) тУ/г). (13)

Последнее выражение показывает, что ионы с г;х<сО/к, для которых усло­вие черенковского резонанса не выполняется ни в одной из точек лармо - ровской окружности (Vx<:V±<CО//с), также обмениваются энергией с коле­баниями. Однако интенсивность обмена (резонансного взаимодействия) экспоненциально спадает с уменьшением V±. Характерный масштаб спа­да Jo/Oi {крI) по порядку величины равен 6y_L~co,/3cОУ9к.

Для выяснения природы резонансного взаимодействия в области ско­ростей V±<(О/к проанализируем выражение для фазы колебаний на тра­ектории иона. Будем отсчитывать время от момента, в который проекция скорости иона на направление распространения колебаний максимальна (их(0)=и±). Тогда при [^«Ссог1 приводим выражение (9) к виду

Ф(£, r(Ј))~const+(—co+kv(0) )T—/cpi(co^)3/3!+... . (14)

В отсутствие магнитного поля (сОг=0, v(Ј)=const) продолжительность че­ренковского резонансного взаимодействия была бы бесконечной. Поворот вектора скорости под действием магнитного поля, учитываемый послед­ним слагаемым в (14), ограничивает время взаимодействия. Если раз­ность Kv±—со достаточно велика, то ион участвует последовательно в двух актах резонансного взаимодействия при T=T8 Lt2=±(2(Kv±—(O)L(Ku±Со»2) )'/а, соответствующих двум точкам черенковского резонанса. С уменьшением VL величина |Tsi—Ts2 “*"0, и при И±— (соД) ^со'/зсо /к зоны резонансного взаимодействия сливаются. Время резонансного взаимодействия в этом случае можно оценить, приравняв последнее слагаемое в (14) единице (6г~со-1/зсог2/а) [70]. Конечность времени резонансного взаимодействия позво­ляет участвовать в нем даже таким ионам, ^-компонента скорости кото­рых во всех точках циклотронной окружности меньше (X)/K(V±<(X)Lk). Действительно, за время Ы колебания не «смогут отличить» ионы с (соД) — (/сб£) от резонансных с V±=CО/к. Поэтому при (сО/к) —

—И±^(д'1з(дУ* /к резонансное взаимодействие остается весьма эффективным. Однако оно резко ослабевает с дальнейшим ростом разности (сO/K)—V± (см. (12), (13)).

Теперь, используя выражение для фазы (14) и формулу (10), рассчи­таем приращение энергии иона с г;х~соД за один оборот по ларморовской окружности:

Aw=—iey (co/coi) 24/зя (/ер*) ",/з Ai (г|),

Где г]=( (со—Kv±)/(Oi) (2/Kpi)4 Процедура, аналогичная использованной в разд. 2, приводит к следующему выражению для коэффициента диф­фузии:

D=N (21крд2/3 (coeqp)2 С0х 1 Ai2 (г).

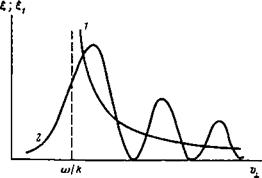
При этом вклад ионов с Kv±~со в изменение энергии колебаний W= =—j DJw описывается выражением вида (8) с заменой подынтегрального множителя £= ((Kv±/(D)2—L)~42 на Б!=л;(4<о/<о<),/з Ai2(г|). Примерные за­висимости ^ на от i;± изображены на рис. 2. Характерные осцилляции величины £1 обусловлены интерференцией двух актов резонансного взаи­модействия, происходящих В Моменты времени £.1 и (см. выше). Упро­щенное выражение £(у±) получается в предположении, что фазы прира­щений энергии иона в моменты времени 1л, Tшг нескоррелированы (вели­чина соз*(Ф (£«1) Ф (£**)) заменяется на 7г). Множитель ^ может быть заменен на £ также, если функция распределения ионов по И± в доста -

Точной степени отличается от б-функции, а именно разброс в значениях поперечной скорости превышает (дч*(д/г/к. В этом случае при интегриро­вании по Осцилляции Величины ^ усредняются.

Заключение

В настоящей работе проанализировано резонансное взаимодействие заряженных частиц с колебаниями в слабом магнитном поле. Показано, что резонансное взаимодействие в этом случае можно рассматривать как черенковское, ограниченное во времени поворотом вектора скорости в маг­нитном поле. Установлены условия, при которых, описывая резонансное взаимодействие, можно вообще пренебречь влиянием магнитного поля. Для этого частота колебаний и поперечное волновое число должны быть достаточно велики (©>©^, Вместе с тем в случае колебаний,

Распространяющихся поперек магнитного поля, функция распределения: частиц по И± должна иметь разброс - б1;х>©,/,©5/в /&х, а «фазовая память» частиц должна быть не слишком продолжительна т<©л-1. Нетрудно по­казать, что яри последние два условия могут быть заменены на

Б17||>©'л©ув /Аг|„ а при учете релятивистской зависимости циклотронной частоты от энергии —на бш>т^2(©^©),/|, где бш — разброс по энергии. Отметим, что заряженные частицы могут считаться незамагниченными вне зависимости от вида функции распределения, если т<©“,/,©т1/*#

ПРИЛОЖЕНИЕ 1

Синхротронное излучение как черенковское в условиях ЭКВРВ. В задачах о ко­лебаниях плазмы, подобных рассмотренной выше, ЭКВРВ обычно не слишком суще­ствен, поскольку он лишь слегка расширяет область резонансного взаимодействия на значения 1>х, меньшие Ш/к±. В то же время имеются ситуации, в которых ЭКВРВ - играет принципиальную роль, обусловливая саму возможность резонансного взаимо­действия. Так, например, поскольку скорость заряженных частиц всегда меньше ско­рости света, черенковское взаимодействие равномерно движущихся заряженных частиц с электромагнитными колебаниями в вакууме невозможно. Если, однако,. 1то, при наличии ускорения за счет ЭКВРВ точное выполнение черенковского резонансного условия становится необязательным. Ускорение может вызываться, например, действием постоянного внешнего магнитного поля. Излучение ультраре - лятивистских электронов, возникающее в этих условиях, принято называть син - хротронным.

Покажем, следуя [3, 4], что, рассматривая синхротронное излучение как черен­ковское в условиях действия ЭКВРВ, можно сравнительно просто интерпретировать

Основные характерные особенности излучения5. Излучение электрона в магнит­ном поле имеет дискретный спектр (й)=л(1>е). Интенсивность л-й гармоники дается выражением

<*/„=(с/2я) | [кА„] |2Я02<Ю, (П.1)

Где До - среднее расстояние от наблюдателя до электрона, вращающегося по цикло­тронной окружиости, - элемент телесного угла,

2я/«,

А„ = (ешв/(2лсЯ0)) ] Йг у(0ехр(1(пй>,*-кК(*)))

-вектор-потенциал, R(f) - траектория электрона.

Предположим для простоты, что ультрарелятивиетский электрон движется по­перек магнитного поля. Тогда, используя выражение для траектории электрона

R(f) = (Х0 + р, sin Yo—P. cos <м; 0),

Находим вектор-потенциал колебании

An=(<?/flo)exp(tkRo)(sin-t0/n(Axpe); (Iv/C)Jn'(K±P.); 0). (П.2)

Здесь 0=kBo; для определенности считается, что колебания распространяются в плоскости X0Z.

Максимум спектрального распределения излучения приходится на высокие гар­моники л=(о/й),» 1. Поскольку рассматриваются ультрарелятивистские электроны, то при не слишком малых углах аргумент функции Бесселя Јj_p»= (g>/g>») (V/C) sin 0» >1, и для самой функции Бесселя справедливо асимптотическое представление (12)' с заменой (о*, pi, К на й>„ р„ К± соответственно. При рассмотрении достаточно боль­ших частотных интервалов du)»(i>, дискретный спектр можно заменить непрерыв­ным: DIn-~DI0=DIn(D(D/(De). Подставляя (П.2) в (П.1) и используя (12), получаем следующее выражение для спектральной плотности излучения:

Й/«=(е2/2яс) (a)2/(Oi) [tg2 0 (2d),/(о) ^*A2i(T|) + (2й),/й))1/*А1'2(т|) ]do>dQ, (П. З)

Где

Л3“ ((*>/2a><)(mec2/w)z + (0 —(я/2))2];

Считается, что v/c»l— (V2) (пгес2/ш)2, W - энергия ультрарелятивистского электрона.

Из (П. З) находим следующие свойства синхротронного излучения. Суммарная энергия, излучаемая электроном в единицу времени, по порядку величины равна /~ (ег/с)&вог(и>/твсг)г, где (йео=еВо/твс - нерелятивистское значение электронной циклотронной частоты. Излучаемые колебания имеют частоту <d~(i>,0{W/Mec2)2 и сконцентрированы в интервале углов Д0~ (тп, с2/ш)«1(0жя/2). Если ультрареляти­вистские электроны движутся не в вакууме, а в плазме достаточно высокой плотно­сти (о)р,^й),о (ш/тпес2), то излучение резко ослабевает (эффект депрессии синхро­тронного излучения). Действительно, при наличии холодной плазмы фазовая ско­рость колебаний возрастает й>//с*»с(1+С/2) (й>р,/й>)2). (Здесь считается й>р,<й>.) В ре­зультате в аргументе функции Эйри в (П. З) появляется дополнительное слагаемое ({Лр«/ш)2((й)/^й)«о) (w/m. c*[71]))^. При выполнении приведенного выше усло­вия оно становится определяющим.

Покажем, что все эти свойства могут быть объяснены сравнительно просто, если синхротронное излучение рассматривать как черенковское, обусловленное ЭКВРВ. Проанализируем выражение для фазы излучаемых колебаний на траектории элек­трона. Заменяя в (14) индекс I на с и используя соотношения kv=(d>/c)i; cos 0* *с[1—(’/г) {Mec2/W)2+ (’/2) (0—(я/2))2],

Р,*»(с/й>,о) (U>/M,C2), (1>е=(1>,о(т. с2/ш),

Получаем

Ф(0® С/2) ((лг, с2/ш)2 + (0— (я/2))2)й>*+ С/в) (с*>/а>«о) (л1,с2/ш)2((1>,о03+ • • •

Приравнивая второе слагаемое единице, получаем оценку максимально возможного времени резонансного взаимодействия (u;//n, c2)J/»(i>-,/,o),o~J/l. За это время элек­

Трон не выйдет из фазы (первое слагаемое по порядку величины не превышает еди­ницу), если (D^(i>,o(W/Mec2)1 (см. выше). Аналогичным образом эффективное резо­нансное взаимодействие возможно лишь, если Д0 = (я/2) —Q^Mec2/W.

Интенсивность черенковского излучения дается выражением

D/« = (c2d)/c) sin2 0cdu>,

Где 0с - черепковский угол. Полагая 0С—Д0, a)*a>eo(u?/m, c2)2, для полной интенсив­ности излучения получаем значение, приведенное выше: 1~(е2/с)(йво(и>/тесг)г.

Присутствие холодной плазмы приводит к увеличению разности Ш/к-и, что ес­тественно затрудняет резонансное взаимодействие электринов с колебаниями. Допол­нительное слагаемое в выражении для фазы колебаний, учитывающее влияние хо­лодной плазмы, имеет вид (‘/2) (й)ре/ш)2*- Оно не сказывается на процессе резонанс­ного взаимодействия, если выполняется условие ((0р«/а>)*6{^1, откуда при а>~ ~а)ей(ш/тесг)г Следует о)р,^а)в0(и;/твсг).

ПРИЛОЖЕНИЕ 2

Ограниченность фазовой памяти иона можио учесть, введя в резонансный знаме­натель в (1) слагаемое 1/х:

V* («) =2-jen *

«) Г Dfo

Вя = 2л(й>р»/*)г ] Dv±------------- Jn2(K9I)

Dv j_ (о—Пй>|+ (i/т)

При мнимая часть е(<> отлична от нуля лишь вблизи гармоник ионной цикло­

Тронной частоты, что характерно для циклотронного резонансного взаимодействия. В обратном предельном случае й>*т<*:1 на зависимости 1те(‘>(й>) отдельные цикло­тронные гармоники не выделяются. Если выполняются условия л» 1, /срг^>1, то Јn(I> - плавная функция номера П и сумма по п в выражении для e(i) может быть заменена интегралом:

00

Ime<<)*=—2л( —^ ^ F Dv±~— F Dn П(а{/п2(кр{)---------------------------- .

' К 1 Dv (<й —П<йг)2 + Т“2

О

Т-1

При о)т^1 множитель------------------------- , рассматриваемый как функция л, имеет вид

(<й—Л<й<)* + Т~2

Узкого пика вблизи значения п=й>/й>*. Поэтому произведение пй>»/я2(Лр<) можно вы­нести из-под знака интеграла, заменив в нем П на а>/а>*. После этого интегрирова­ние по Dn приводит к (4).