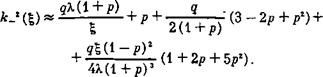ФИЗИКА ПЛАЗМЫ

ЭЛЕКТРОННЫЙ ЦИКЛОТРОННЫЙ РЕЗОНАНС ДЛЯ ЭЛЕКТРОМАГНИТНЫХ КОЛЕБАНИЙ, РАСПРОСТРАНЯЮЩИХСЯ ПОД УГЛОМ К НЕОДНОРОДНОМУ МАГНИТНОМУ ПОЛЮ

А. В. ТИМОФЕЕВ, Г. Н. ЧУЛКОВ Введение

Как известно, в плазме, помещенной в магнитное поле, могут распрост­раняться высокочастотные колебания двух типов. В плазме не слишком высокой плотности, когда выполняется условие (0ре<(0, (о)Рв — плазменная электронная частота, ш, — электронная циклотронная частота), их класси­фицируют как обыкновенные и необыкновенные волны. Если магнитное поле однородно, а температура плазмы равна нулю, то обыкновенная вол­на с частотой ш, равной электронной циклотронной сое, не «чувствует» элек­тронного циклотронного резонанса. Эта особенность - в поведении колеба­ний объясняется тем, что при й)=(о, колебания обладают круговой поляри­зацией, причем электрический вектор вращается в ионную сторону (см., например, [1 ]). Точно так же ведет себя и необыкновенная волна, распро­страняющаяся под углом (как угодно малым) к однородному магнитному полю. В то же время у необыкновенной волны, распространяющейся строго вдоль магнитного поля, направление вращения электрического вектора ме­няется на обратное, и поэтому такая волна испытывает сильное затухание.

Если магнитное поле неоднородно, то резонансное циклотронное взаи­модействие ограничено окрестностью резонансной точки г8, в которой вы­полняется условие (о=(о,(гв). В этой области дисперсионные свойства плаз­мы резко меняются, поэтому, проходя через нее, колебания не только меняют свою амплитуду (частично поглощаются), но могут также и отра­жаться. До сих пор влияние неоднородности на резонансное взаимодейст­вие было исследовано лишь в случае колебаний, распространяющихся вдоль магнитного поля, о котором предполагалось, что его величина также меняется в продольном направлении [2] (см. также обзорную работу [3]). Оказалось, что обыкновенная волна по-прежнему «не чувствует» цикло­тронного резонанса. Для необыкновенной волны были найдены коэффици­ент поглощения при ее прохождении через резонансную область и коэф­фициент отражения от этой области.

В настоящей работе, как ив [*], рассматривается магнитное поле, ме­няющееся в продольном направлении, в то же время угол между волновым вектором колебаний и магнитным полем вдали от резонансной точки счи­тается произвольным. Рассмотрение, однако, показывает, что при подходе к резонансной точке продольная компонента волнового вектора неограни­ченно возрастает — волна как бы выпрямляется вдоль поля. Волны, бегу­щие вдоль поля, уже могут резонансно взаимодействовать с электронами. Эта особенность поведения колебаний в окрестности резонансной точки отмечалась в ряде работ (см., например, [4> 5]). В настоящей работе пока­зано, что описанный выше эффект «выпрямления» имеет следствием резо-

Ыансное взаимодействие необыкновенных колебаний с плазмой. В то же время он не сказывается на распространении обыкновенных колебаний. Мами найдены коэффициенты поглощения и отражения необыкновенных колебаний, падающих на резонансную точку. Эти результаты могут счи­таться обобщением полученных в [[55]] на случай произвольного угла паде­ния колебаний по отношению к магнитному полю.

1. Основные уравнения

Рассмотрим электромагнитные колебания, распространяющиеся по плазме, помещенной в неоднородное магнитное поле. Будем использовать декартову систему координат, причем ось OZ направим вдоль магнитного поля, а ось ОХ таким образом, чтобы волновой вектор колебаний лежал в плоскости XOZ. Начало координат выберем в резонансной точке г„ где электронная циклотронная частота (ов(гв) совпадает с частотой колеба­ний со.

В силу стационарности плазмы и ее однородности в поперечном на­правлении в ней могут распространяться волны вида Е(г) =Е(z) exp-

• I— i(ot+ikj_x]. Подставляя это выражение в волновое уравнение и выражая из его z-й компоненты Ez(Z) через Ex(Z), приводим две остальные компо­ненты уравнения к виду:

TOC o "1-5" h z Е-"+а. Е-+ЬЕ+=0, (1)

Е+"+а+Е++ЪЕ.=0. (2)

Здесь введены следующие обозначения: E~=Ex—iEUy

1 г, , - г, 2?(1 + р) 2? / 2Р

-ЕХ+1Е„ а-= ^ — (i-P + —s

2qp ( 2 2qp(i—p)Q

A+ = p + —HIL{l-p--------------------- - Л, B =

F 1 + P F 1 + Й /

TOC o "1-5" h z 1 - f P 1 + Q / (1 + /?)(1 + Q')

1—2q — nx* (Dpe2 _ 0)2

----------- 1 Ј —--------- .,

1 — 2q 2(оег о

пм=>кхс/(о; штрих означает дифференцирование по £. Плазма считается холодной, и для тензора диэлектрической проницаемости используются известные выражения (см., например, [*])•

Цитируемую там литературу), колебания трансформируются друг в друга в той точке, где значения их волновых векторов совпадают. Причем если точка трансформации смещена с действительной оси в комплексную плос­кость на расстояние а характерное волновое число колебаний ~к>Ь~ То коэффициент трансформации экспоненциально мал ~ехр (—КЬ). Факти­чески в этом случае одна волна превращается в другую не в одной точке, а на расстоянии ~Ь и интерференция гасит появляющиеся при этом коле­бания. Для колебаний, рассматриваемых нами /с~со/с, а Ь по порядку ве­личины совпадает с характерным масштабом изменения магнитного поля, поэтому в практически интересных случаях коэффициент трансформации ~ехр (—КЬ) намного меньше коэффициентов поглощения и отражения колебаний в точке циклотронного резонанса (см. ниже). Ограничивая себя задачей изучения резонансного циклотронного взаимодействия, мы не бу­дем затрагивать эффектов трансформации колебаний.

В малой окрестности резонансной точки

|а_|>а+, Ъ для КТ2 можно использовать упрощенные выражения:

Здесь верхний знак соответствует необыкновенным колебаниям, нижний — обыкновенным. В рассматриваемом приближении эти колебания распрост­раняются независимо друг от друга и им можно сопоставить несвязанные волновые уравнения второго порядка. Волновое уравнение, описывающее распространение необыкповенных колебаний, близко по виду к уравне­нию (1):

(5)

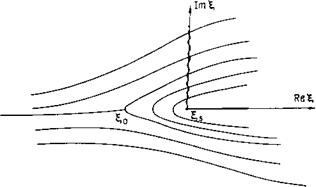
Его удобно исследовать, рассмотрев аналитическое продолжение решения на плоскость комплексных значений | (см., например, [7]). Предположим, что магнитное поле в окрестности резонансной точки меняется монотонно. В этом случае рис. 1 дает картину линий действительной фазы квазиклас - сических решений уравнения (5). Линии действительной фазы начинают­ся в точках £3=0 и |0, поблизости от которых квазиклассическое представ­ление решения становится неприменимым &(Ы=0°, &(Ы=0. Точку £0 можно назвать обычной точкой поворота, точку — сингулярной точкой поворота. Поскольку |в является особой точкой волнового уравнения, из нее проведен разрез, изображенный на рис. 1 волнистой линией. Его распо­ложение определяется правилом обхода Ландау. В окрестпостях точек |в и £0 решения уравнения (5) выражаются через функции Бесселя. Чтобы продолжить решение через точки и его асимптотики по разные сто­роны от этих точек сшиваются с квазиклассическими представлениями решения. Мы не будем излагать эту хорошо известную процедуру. Приве­дем лишь конечный результат. Колебания, падающие на резонансную точ­ку справа (со стороны большего магнитного поля), проходят через резо­нансную область без отражения, уменьшив свою амплитуду в ЕлА раз, где

Нетрудно заметить, что коэффициент прохождения

Равен коэффициенту подбарьерного просачивания через область непроз­рачности (|0, 0). Колебания не отражаются от правой границы этой обла­сти — сингулярной точки поворота |8, поскольку в этой точке происходит поглощение энергии колебаний, учитываемое правилом обхода Ландау (см.

[2] ). Прошедший, отраженный и поглощенный потоки энергии будем ха­рактеризовать коэффициентами т, р и г]=1—■т—р. Для колебаний, падаю -

TOC o "1-5" h z Т=6Г-2ЯА, (6)

Р=о, О)

Т]=1—е~2з1А. (8)

Для того чтобы при анализе проникновения колебаний через область

Непрозрачности (£0, 0) можно было использовать квазиклассическое при -

О

Ближение, должно выполняться условие ПА = ^ 1&(£) |<2£>1. Квазиклас -

*0

Сическое представление решения, как известно, является асимптотическим. Неизбежная неточность асимптотического представления в области £>0 превышает амплитуду прошедшей волны. Поэтому, оставаясь в рамках

Квазиклассического приближения, следовало бы считать, что колебания, падающие со стороны большего магнитного поля, поглощаются целиком 11=1; т=р=0. Мы, однако, привели выражения (6)— (8), поскольку на самом деле они применимы и при ПА^ 1 (см. следующий раздел).

Колебания, падающие со стороны меньшего магнитного поля, сначала попадают на обычную точку поворота |0, коэффициент отражения от ко­торой в квазиклассическом приближении равен р=1. Коэффициент про­хождения в область |>|8 по-прежнему дается (6). Кажущееся несоответ­ствие с законом сохранения энергии следует отнести на счет неточности квазиклассического представления (см. выше).

Используя квазиклассическое приближение, мы приходим к выводу, что колебания, падающие со стороны большего магнитного поля, целиком поглощаются, а падающие со стороны меньшего — отражаются, поэтому конкретное значение величины А оказывается несущественным. Однако для сопоставления с результатами следующего раздела мы вычислим его в предположении 1. При выполнении этого условия размер области не­прозрачности мал по сравнению с характерным масштабом изменения маг - с

Нитного поля —Поэтому мы можем аппроксимировать зави­сав

Симость магнитного поля от координаты Г = — £ линейной функцией

Со

0=<ое(|)/<о = 1+|/А,, где К=Ь(о/с. Разложение &-2(£) по малому отношению

Имеет вид:

Поскольку при интегрировании по д, в выражении А =— I к{%) иг-

Л •*

60

Рают роль характерные масштабы то разложение К_2 по УК пе­

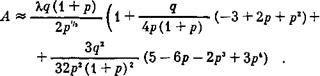Реходит в разложение Л по д:

(Ю)

Что касается обыкновенных колебаний, то их волновое число К- в ин­тересующей нас области 151 почти постоянно (см. (3)), а резонансная точка является регулярной. Отсюда следует, что обыкновенные колебания должны проходить через резонансную область без поглощения и отра­жения.

3. Приближение

Из (10) следует, что квазиклассическое приближение становится не­справедливым при достаточно малых значениях Q. Рассмотрим проблему в этом случае. Систему уравнений (1), (2) можно свести к одному уравне­нию четвертого порядка, причем уравнения завязываются через последние слагаемые (1), (2). Если их опустить, то мы приходим к двум независи­мым уравнениям для Е- и /?+. Нетрудно сообразить, что этому приближе­нию соответствует игнорирование в полном уравнении четвертого порядка слагаемых, пропорциональных малой величине Qг< 1. В настоящем разделе мы будем использовать это приближение. Уравнение четвертого порядка проанализировано в Приложении.

Опустим в уравнении (1) последний член, а в выражении для А~ — сла­гаемые, пропорциональные д£/Я. При этих упрощениях уравнение (1) мо­жет быть представлено в виде уравнения Уиттекера:

(И)

Здесь введена новая координата £і = 2Ір

Висимость Й(£) аппроксимирована линейной функцией Й=1+£/А,. Вели­чина А с точностью до членов порядка д2 совпадает с (10).

Решения уравнения (11) удобно выразить через вырожденные гипер - геометр"ические функции (см., например, [*]). Их асимптотики при Ц||-*- имеют вид экспонент с быстро меняющейся фазой, т. е. описывают бе­гущие волны. Сопоставляя амплитуды отдельных волн при различных значениях находим коэффициенты прохождения т, отражения р и по­глощения т]. Для колебаний, падающих со стороны большего магнитного поля, приходим к формулам (6) —(8), а для колебаний, падающих со сто­роны меньшего поля, получаем

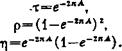(12)

(13)

(14)

В том же приближении (<г=0) распространение обыкновенных колеба­ний описывается уравнением (2) без последнего слагаемого. Из него сле­дует, что обыкновенные колебания свободно проходят через резонансную область.

Сопоставление результатов, полученных в настоящем и предыдущем разделах, показывает, что приближение д2=0 справедливо при Хд3<1. Если выполняется условие Хд3<1, но Хд» 1 (Л>1), то результаты, найденные разными методами, совпадают.

Выражения (6) —(8), (12) —(14) были впервые получены в [2] для слу­чая продольного распространения колебаний (гс±=0, р=1). По существу мы показали, что после соответствующего переопределения величины А их можно использовать при произвольном угле падения колебаний по отноше­нию к магнитному полю. Поскольку величина А возрастает с увеличением п± из (6) —(8), (12) —(14) следует, что Колебания, распространяющиеся под большим углом к магнитному полю, более интенсивно взаимодейству­ют с электронами (коэффициент прохождения падает). По-видимому, уси­ление взаимодействия объясняется увеличением времени пребывания вол­нового пакета в резонансной зоне.

Поляризацию колебаний удобно определить из у-й компоненты волно­вого уравнения, которую в квазиклассическом приближении можно пред­ставить в виде:

Ех —- ГСц2 + £уу /лг

Т"---------- 8 • (15)

Ь У С Ху

Из (15) и (1) находим, что Иц2«Яд(1 +/?)/£» гху=—гдАД при £-*-0.

Из этих выражений следует Ех/Еу&—£ (1—гсх2), т. е. рассматриваемые коле-

Бания обладают эллиптической поляризацией, причем электрический век­тор вращается в электронную сторону. Если 0, то поляризация перехо­дит в круговую. Этот анализ показывает; что эффект «выпрямления», о котором говорилось во введении, действительно приводит к изменению поля­ризации колебаний по сравнению со случаем однородного магнитного поля.

Аналогичным образом можно показать, что поляризация обыкновенных колебаний в точке циклотронного резонанса является круговой, причем электрический вектор вращается в ионную сторону.

В настоящей работе считалось, чю магнитное поле меняется в продоль* ном направлении. Такие конфигурации характерны для открытых магнит­ных ловушек. Однако и в этом случае условие НЦУЯ выполняется строго лишь на оси системы. Чтобы ответить на вопрос: при каких углах 0 между Н и V# наше рассмотрение останется справедливым, необходимо вспом­нить, что циклотронный резонанс переходит в плазменный при 6=^0, при­чем условие плазменного резонанса при 0^1 имеет вид со. гее « со —02

Со

(см., например, [4]). Естественно ожидать, что циклотронное резонансное взаимодействие будет происходить так же, как и при 0=0, если выполня­ется условие А:хта*Ув> | сое гва—© |, где ив — тепловая скорость электронов,

Оценку для кг Те1х~ ^(I + р)1'1 получаем с помощью уравнения (5),

V С 1 В

Считая в нем ыг/Ь~кгтахив. Используя это выражение, получаем 0то*« «(17./дс),/‘(1+^),/#.

ПРИЛОЖЕНИЕ

Система уравнений (1), (2) может быть проанализирована еще одним способом. Примем й= 1+1/А, и положим Й»1 всюду, кроме резонансного знаменателя в урав­нении (1). При этих предположениях система сводится к следующему уравнению четвертого порядка:

5(£+1^+о£:+'Ч^+)+Я(д(-г^"+б£+)=0, (П.1)

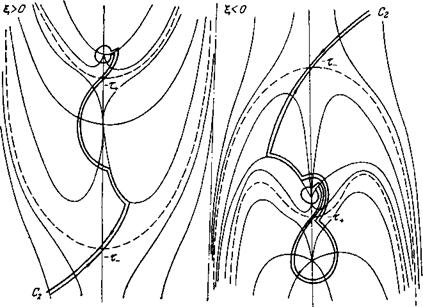
Вторая точка перевала - т+ при изменении знака £ также остается на мнимой оси, смещаясь по ней на малое расстояние порядка gl/X. При этом она не выходит за пределы отрезка (-*+; -*-)• На нем модуль V(t) не меняется, а следовательно, будет постоянной и амплитуда обыкновенных колебаний. Отраженным колебаниям, если бы они существовали в данном случае, соответствовали бы точки перевала, ле­жащие в верхней полуплоскости. Из рис. 3, 4 следует, что контуры интегрирова­ния в верхнюю полуплоскость не заходят, и поэтому отражения колебаний не про -

Исходит. Таким образом, анализ упрощенной сингулярной системы уравнений показывает, что колебания, падающие со стороны большего магнитного поля, ме­няют свои характеристики при прохождении резонансной точки в соответствии с формулами (6)-(8). Аналогичный результат получается и для колебаний, падающих слева (со стороны меньшего магнитного поля). Рассмотрение в этом случае несколь­ко усложняется ввиду появления отраженной волны.

Проведенный анализ также подтверждает вывод, сделанный в разделе 2, о не­зависимом распространении обыкновенных и необыкновенных колебаний, несмотря на связь между уравнениями (1), (2). Следствием такой связи является лишь на­рушение однозначного соответствия, при котором обыкновенные колебания можно было описать с помощью Е+, положив £_=0, и наобброт.

Институт атомной энергии Поступила в редакцию

Пм. И. В. Курчатова 29 июля 1977 г.

Исправленный вариант получен

2 февраля 1978 г.