О ЦИКЛОТРОННОМ НАГРЕВЕ В КОРОТКИХ АДИАБАТИЧЕСКИХ ЛОВУШКАХ л. в. ТИМОФЕЕВ
Введение
Электромагнитные колебания, электрический вектор которых перпендикулярен постоянному магнитному полю, изменяют энергию ларморов - ского вращения заряженных частиц. Если колебания обладают круговой поляризацией, то для скорости ларморовского вращения нетрудно получить следующее уравнение:
ЕЕ
171
Здесь ф(0=^(0~1|)(г) — фаза ларморовского вращения, ш — частота электромагнитных колебаний.
При циклотронном резонансе в однородном магнитном поле фаза <р(*) остается постоянной, и поэтому и± меняется так, как если бы магнитное поле вообще отсутствовало. В адиабатических лозушках магнитное поле неоднородно. Движение между пробками ловушки вызывает изменение фазы. Каков будет результат взаимодействия заряженных частиц с электромагнитными колебаниями в этом случае,— заранее сказать невозможно. Изучение вопроса, проводившееся в течение ряда лет, показало, что характер взаимодействия существенно зависит от длины ловушки I. Здесь под длнной ловушки мы подразумеваем размер области, занятой плазмой в направлении вдоль магнитного поля. При магнитном удержании Ь—Ьи^/и^, где Ь — характерный масштаб изменения магнитного поля в продольном направлении, значки «продольно» и «перпендикулярно» отмечают направление относительно магнитного поля, нуль — значения величин в минимуме магнитного поля. Ловушку будем называть короткой, если заряженная частица (для определенности будем в дальнейшем иметь в виду электроны) за время одного прохождения по ловушке не успевает выйти из резонанса с волной Дср<л, и длинной, если зона резонансного взаимодействия занимает малую часть системы. Оценки показывают, что ловушку следует считать длинной, если выполняется условие />(£гс) и короткой — в обратном случае — /< (Ьгс) ч где ге — ларморовский радиус электрона.
Состояние проблемы циклотронного нагрева в длинных ловушках было проанализировано в работе [[54] ]. Для таких систем наиболее существенно, что в них даже регулярные циклотронные колебания могут хаотизировать фазу <р(*) в уравнении (1). В результате изменения и± под действием циклотронных колебаний становятся хаотическими, что, естественно, ведет к увеличению средней энергии ларморовского вращения, т. е. к нагреву плазмы.
|
913 |
![]() Взаимодействие заряженных частиц с циклотронными колебаниями в коротких ловушках /<(Lгe),/, рассматривалось в работе [*]. Было показано, что если частота колебаний равна минимальной циклотронной на не-
Взаимодействие заряженных частиц с циклотронными колебаниями в коротких ловушках /<(Lгe),/, рассматривалось в работе [*]. Было показано, что если частота колебаний равна минимальной циклотронной на не-
7 Физпка плазмы, шип. 4
Которой силовой линии магнитного поля, то часть электронов, движущихся по этой силовой линии, захватывается колебаниями Это означает, что электрон начинает вращаться по ларморовской окружности не с локальной циклотронной частотой, меняющейся в ловушке от точки к точке, а с фиксированной частотой электромагнитных колебаний. В результате фаза Ф в (1) становится постоянной величиной, а следовательно, захваченные электроны вовлекаются в режим непрерывного ускорения, не чувствуя неоднородности магнитного поля.
Для обычных адиабатических ловушек условие /> (Ьге) ',г выполняется с большим запасом, поэтому их в указанном смысле следует считать длинными. Вместе с тем электроны с малыми значениями Уц0 движутся вблизи минимума магнитного поля на данной силовой линии, т. е. как бы находятся в короткой ловушке. В соответствии со сказанным при циклотронном нагреве в адиабатических ловушках следует ожидать, что основная масса электронов будет нагреваться посредством стохастического механизма. Эти электроны увеличат свою энергию сравнительно слабо. В то же время малая доля электронов, локализованных вблизи минимума магнитного ПОЛЯ на ТОЙ СИЛОВОЙ ЛИНИИ, где выполняется условие й)е тп»п = Юг будут нагреты значительно сильнее. Подразделение электронов на две фракции часто наблюдается в экспериментах по циклотронному нагреву (см., например, [3]). Появление при циклотронном нагреве группы высокоэнергичных электронов, локализованных в минимуме магнитного поля, было использовано в [4] для стабилизации дрейфово-конусной неустойчивости. С тем же самым явлением естественно связать прожог лайнера, наблюдавшийся в экспериментах на установках типа токамак (см., например, [*])• Действительно, в [•] было показано, что в этих установках возможно возбуждение циклотронных колебаний. Если предположить, что эти колебания взаимодействуют с электронами так же, как и в адиабатических ловушках, то в гофрах магнитного поля токамака должен образовываться тонкий слой высокоэнергичных электронов. Такие электроны,, выдрейфовывая наружу и высаживаясь на лайнере, могут вызвать его прожог. В пользу этой гипотезы говорит форма и расположение отверстий в лайнере.
В настоящей работе рассмотрен ряд вопросов, возникающих прп попытках связать перечисленные выше экспериментальные результаты с явлением захвата и непрерывного ускорения электронов, исследовавшимся в работе [*]. Рассмотрение влияния кулоновских соударений на ускорение захваченных электронов показало, что в этом случае возможно явление просвиста. Найдено также, что в зависимости от конкретных условий ускорение захваченных электронов может ограничиваться следующими факторами: неточное равенство частоты электромагнитных колебаний минимальной циклотронной частоте на данной силовой линии, нестабильность частоты циклотронных колебаний, релятивистская зависимость циклотронной частоты от энергии ларморовского вращения, эффект когерентного синхротронного излучения и, наконец, неустойчивость плазмы. Нами уточнены также условия, которым должны удовлетворять электроны, вовлекаемые в процесс ускорения.
Нии мы их можем не учитывать. Ъудем также считать электрическое поле колебаний однородным в пространстве. Это упрощение, но влияя на существо дела, позволяет сократить выкладки. При сделанных предположениях гамильтониан электрона имеет вид (см. [2 7]) 1
Ф=М<о..-<о)+г,(^)/+-^-(^)/'с03(<р-^3т2?). (2)
Здесь ц, ф и л» ? ~ Две пары канонических переменных, к=ти±/2юе — магнитный момент, ф — разность между усредненной по продольным колебаниям (по [}) фазой ларморовского вращения и фазой электрического поля, г=тЬи\0г/2и±0 имеет смысл продольного инварианта, р — фаза продольных колебаний.
Предположим, что фаза продольных колебаний [} меняется быстрее ф, тогда гамильтониан (2) можно усреднить по £
Здесь /0 — функция Бесселя нулевого индекса. В (3) переменными являются (1Иф, аг] входит в него в качестве параметра.
Электрическое поле выпадает из усредненного гамильтониана (3) при ц=цп (п=1,2,3,...), где Цп=г)/4хп, /0(Яп)=0. На частицы с ц=цп электрическое поле не действует, и поэтому их магнитный момент не меняется. Отсюда следует, что траектории частиц на фазовой плоскости ц, ф не могут пересечь линий ц=цп. Наиболее высоко расположена линия Ц=Ц1. В области Ц>Ц1, вообще говоря, возможно неограниченное ускорение частиц. Проанализируем эту возможность. Поскольку при движении гамильтониан должен оставаться постоянным, то для обращения ц в бесконечность необходимо выполнение двух условий: 1) частота колебаний. должна быть равной ю. о, 2) электрическое поле должно превышать критическое значение Е0=(от)/е£ или в другом виде:
Ео=Н0и{{ ог/си± о - (4)
Эти два условия, как легко показать из анализа траекторий на фазовой плоскости (см. также [2]), являются и достаточными.
В области больших значений ц (ц>4т)) характер движения становится очень простым. Действительно, полагая /0(г]/4ц) =1 и учитывая определения ц, ф, нетрудно показать, что уравнение движения, получаемое из (3), приводится к (1). Из условия <ф>=С0П81 следует ф = агСС08 ( — Г](оЬ/
У. -*00
/еЕ)= сог^. Таким образом, в соответствии с (1) заряженная частица увеличивает свою энергию так, как если бы она находилась лишь в одном постоянном электрическом поле. Этот результат вполне понятен, так как частицы с большим значением ц (ц>т]) находятся в минимуме магнитного поля, где о)в(г) «о)в о=«. Следует, однако, отметить, что как бы близко к минимуму магнитного поля ни двигался электрон, он входит в режим непрерывного ускорения лишь в том случае, если электрическое поле превышает критическую величину (4). Она может быть получена из следующих простых соображений. Электрон непрерывно ускоряется вол - ной, если его фаза не меняется во времени. К изменениям фазы ф может привести движение вдоль магнитного поля, поскольку циклотронная частота меняется в продольном направлении. При £-*0, й)=й)е0 фаза ф
Колеблется с частотой12 = -— <£> = 11 Ые а/2т^2),/1=<(ое>= — о>е0(^цо/^_1_о)
А1 2
Электрическое поле изменяет и±с, а следовательно, и £2. Очевидно, что эффект расфазировки может отсутствовать, если частота & существенно изменится за время, меньшее Й~ т. е. будет выполнено условие: £2/Й= =2у±/и1=2еЕ1ти±>£1. В этом случае в силу увеличения и±0 электрон «затягивается» в минимум магнитного поля, т. е. к резонансной точке, быстрее, чем успевает накопиться фазовое рассогласование, достаточное для выхода из резонанса. Отметим, что получаемое таким образом критическое значение электрического поля лишь численным множителем отличается от найденного выше (см. (4)).
Рассмотрение, проводившееся в предыдущем разделе, основано на использовании гамильтониана, усредненного по продольным колебаниям электрона в ловушке (координате [}). Такое усреднение законно, если выполнены два условия: координата меняется значительно быстрее, чем Ф, и в гамильтониане отсутствуют секулярные слагаемые, соответствующие резонансам /?ф—gj}=const. Для выделения таких слагаемых используем известное разложение:
Sm(q>--^J-sin2ij)= (-^-)sm(<p-2gЈ).
Я
Из этого выражения следует, что секулярные члены появляются, если выполнено условие Й=Й_1_—й)=2д£2ц, где q — целое число,
Йх■ W L.”“* ■■ (1+т(2,шш* •> ■* )-“••(■1+2^) •
Аф I _ 1 / 2цш. о ',г
Условие резонанса можно представить также в виде ц=т]/4д.
Вопрос о движении в области малых значений ц рассматривался в работах [•—10], Где использовалась общая теория возникновения стохастич - ности в многопериодических системах.
Было найдено, что при достаточно большой амплитуде электрического поля происходит так называемое явление перекрытия резонансов, в результате которого движение частиц по фазовой плоскости ц, ф хаотизи - руется. В [•■ *■4] рассматривалось движение частиц с ц<т]/4, которые могут заходить далеко от минимума магнитного поля 1^>(Ьге)ъ (случай длинных ловушек). Результаты, полученные в [10], пригодны в промежуточном случае ji*r|/4g (l~l/i(Lre/q)lli), где q — целые числа порядка единицы. Условия возникновения стохастичности, полученные в этих работах, имеют вид:
Соответственно. Они совпадают на границе области применимости.
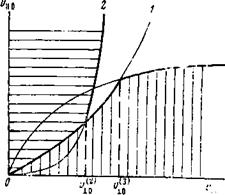
Полезно области стохастического нагрева и нагрева в режиме захвата волной (детерминированный нагрев) нанести на плоскость v±0, z>n *. Стохастически могут нагреваться лишь электроны с достаточно большой продольной скоростью vno^v*ЈQ(La>eo)-','(l'^(Lre) :)t в то время как для за-
|
Хвата необходимо выполнение обратного условия К М Г ПЛТПГТГТТЛЛ ПТТЛТГ/Ч*т*ж/ч *« ^ »Г1 Ч / Т * V — */ 2 |
|
(1^(Ьге)'2). Граничное значение у„ (Ьыс 0) Сунке кривой 1. Критерии стохастич- Ности и захвата также можно пере- >у_і_3 ОС'7, (ю, ОЬ) -5/* ^0,14 1 , Рой (см. (4)) Уцо<(Ухо с)Чг(Е/Н)ъ. На плоскости и± 0, ум 0 они ограничи- |
|
ДУ В заключение сопоставим коэффициент стохастической диффузии с коэффициентом диффузии, возникающей под действием кулоновских соударений. В [1 ] для первой величины в предельном случае очень длинных ловушек было получено следующее выражение: Я£«45а), 0(сЕ/Н)2(Ухо/у„ о)4/3а/г.) Коэффициент столкновительной диффузии естественно принять равным Г^^сут2, где ут —тепловая скорость электронов. Если принять Ге=10 эв, £=100 в/см, Я=3-103 гс, й) = (1/г)-Ю11 сек~ п=1012 см~ то Г>Е будет превышать Б* примерно на 5 порядков. Заметим, что циклотронные колебания В отличие ОТ столкновений меняют ЛИШЬ Ухо. 3. Явление ^просвиста» Как известно, под действием достаточно большого постоянного электрического поля электроны незамагниченной плазмы входят в режим непрерывного ускорения, которому не могут помешать кулоновские соударения (режим «просвиста») (см. [13> 14]). Очевидно, что то же самое будет иметь место, если плазма помещена в постоянное магнитное поле, параллельное электрическому. Хотя электрическое поле циклотронных колебаний перпендикулярно магнитному, однако непрерывное ускорение электронов возможно и в этом случае (см. выше). Появление просвистных электронов облегчается тем, что электрическое поле циклотронных колебаний может достигать сравнительно больших величин, на 2—4 порядка превышающих величину постоянного электрического поля, которое можно поддерживать в незамагниченной плазме или при Е||Н. Однако, с другой стороны, непрерывно ускоряются лишь те электроны, вектор скорости которых почти перпендикулярен магнитному полю, поэтому даже слабые возмущения могут прервать процесс ускорения. |
|
Область стохастического нагрева заштрихована горизонтально, область захвата и детерминированного нагрева — вертикально |
|
Ординат Ух»/у±о ~ (0,14),,; Этому Численному коэффициенту не еле дует придавать строгого смысла, поскольку, во-первых, он был получен с помощью критерия стохастичности Применимого ДЛЯ очень ДЛИННЫХ ловушек (кривая 2 при У||0-^°°), во-вто - рых, в соответствии с [!1,12] само явление перекрытия резонансов, ведущее к стохастичности, не имеет четко определенного начального момента. Тем не менее мы надеемся, что он правильно отражает соотношение меж- |
|
(2) |
|
(3) И Ухо |
|
(2) Ухо |
|
|
|
|
 |
|
TOC o "1-5" h z при анализе ьлиннии л^шпив^ппл. ..................... ^ ^ 4_ _
(см., например, [14]) ^
-1<(д„ )’>=2у.— . (5)
& и±0
Здесь V, — частота кулоновских соударений электронов, движущихся
С тепловой скоростью!7Т.
Сi еЕ (1
Учитывая (1), произведем в (5) замену — =----------- ‘г----- Интегрируя
СИ пъ иУ | 0
(5), получаем приращение дисперсии Уцо при увеличении поперечной скорости от ит до и± 0:
< (Ду,, „) ’> »,*1п (. (6)
Поскольку дисперсия в значениях V)) о в функции от и± о возрастает по
Логарифмическому закону, а продольное значение у,, 0 — по степенному
•/* ^ (3) V* (3^
При и±о<и±0 и и„0~и±о при и±0>и±о, то явление «просвиста» должно иметь место. Последовательность процессов, приводящих к «просвисту», такова: посредством стохастической диффузии электроны подаются на границу области непрерывного ускорения, после чего электрическое поле уводит их в «просвист». Причем режим «просвиста» начи
Нается с
|
О |
![]() ^*(ттт) при А^т)
^*(ттт) при А^т)
И С И± при Если И±о имеет меньшее значение, то
Влияние кулоновских соударений преобладает над влиянием электрического поля.
4. Факторы, ограничивающие ускорение электронов
А) В адиабатических ловушках магнитное поле неоднородно как в про
Дольном, так и в поперечном направлениях. Поэтому резонансное условие ш=(!)«,„»»„ может быть выполнено лишь на какой-то фиксированной магнитной силовой линии. Рассмотрение показывает, что максимальная скорость, которую могут достичь электроны при равна и±отах*
ЕЕ
»------ 16©!"1, где бй)*=ш—го. о. Эта оценка может быть получена из
Т
Сравнения первого и третьего слагаемых в гамильтониане (3).
Б) Мы считали, что электромагнитные колебания монохроматичны. Однако в действительности спектральная функция любых колебаний имеет некоторую конечную ширину Дю, и поэтому приближение монохроматических колебаний пригодно лишь при б£<(Дй))-1. За время (Д©)"1 поперечная скорость и±0 изменится на величину еЕ/т(&(а)~1. На больших интервалах времени изменения и±0 будут иметь диффузионный характер с шагом еЕ/т(Дм)-1.
В) Расфазировка между электромагнитными колебаниями п ларморов - скпм вращением электронов, приводящая к ограничению ускорения, может также вызываться релятивистской зависимостью циклотронной частоты от скорости. В этом случае максимальное значение скорости опре-
ЕЕ 1
Деляется соотношением 0«--------- ' (с/и± о) 2, откуда следует о та*«
ТТЬ 00« о
&с(Е/Н)'и. Аккуратное рассмотрение вопроса, проведенное в ряде работ (см., например, [|9]), подтверждает эту оценку.
Г) Как было показано в разделе 1 настоящей работы, электроны, захватываемые волной, приобретают одно и то же значение фазы ларморов - ского вращения <р. В результате в области ©е(г)«й)св образуется узкий
Слой сфазированных электронов. Его продольный размер (толщина) довольно мал Z<(Lrt.)'/j, а поперечный зависит от поперечной неоднородности магнитного поля (см. выше). Синхротронное излучение электронов в этом слое будет когерентным. Можно представить себе такое равновесное состояние, при котором вся энергия, приобретаемая электронами от циклотронных колебаний, затрачивается на синхротронное излучение. При этом необходимо различать две возможности в зависимости от соотношения между длиной волны излучаемых колебании Я=2ли поперечным размером слоя 1±. Если kl±<.i, то электроны излучают когерентно по всем направлениям. Приравнивая энергию, получаемую от внешнего поля NeEvю, излучаемой Nze2wzv±0z/c3 (см., например, [1в]), находим v±0max~ ~с(Е/Н) (mc3/ez(щeN), где N — полное число электронов в слое. Прп выполнении обратного условия kl_L> I фаза излучаемых колебаний будет постоянной в пределах слоя ускоренных электронов лишь тогда, когда волновой вектор колебаний наклонен к магнитному полю под достаточно малым углом 0<1/А:/х. В этом случае имеем v±0 maxжc (Е/Н) (mcVeW9s). Интересно отметить, что в [в] появление ускоренных электронов, активно взаимодействующих со стенкой, сопровождалось мощным синхротронным излучением.
Д) Под действием электрического поля циклотронных колебаний возрастает лишь поперечная компонента скорости. Поэтому распределение электронов по скоростям в окрестности минимума магнитного поля должно быть анизотропным, что может привести к неустойчивости. Если плотность плазмы достаточно низка ((ор.<ш,), то неустойчивыми могут быть электромагнитные колебания с законом дисперсии &~кс. Такие колебания будут усиливаться при прохождении через слой анизотропных электронов, если выполняется условие VX0^ (VrCriolni)'1*, где п0 — плотность плазмы, ni — плотность электронов, захваченных-волной. Критерий усиления легко получить из рассмотрения, аналогичного проведенному в [17]. Приведет ли такое усиление к установлению собственных колебаний, нарастающих во времени, зависит от состояния плазмы в остальной части системы п от граничных условий. В плотной плазме (1)ре>72(0. существует опасность раскачки потенциальных колебаний (см., например, [18]). Развитие той
Или иной неустойчивости может привести к разрушению слоя анизотроп
Ных электронов.
Институт атомной энергии Поступила в редакцию
Им. И. В. Курчатова 8 октября 1977 г.