Динамика замедления отдельного иона
Движение отдельного иона можно описать следующими уравнениями
^- = а,[УЬ]-Т1г^т/(г). (15>
Здесь о) = -^----------- циклотронная частота ионов в магнитном поле//; Ь —
Единичный вектор, направленный вдоль магнитного поля. Правая часть уравнения (15) учитывает силу трения, действующую на ион, когда он
Находится В дуге Рхр. =-------------- , где величины т19 [а(х)
Были определены в предыдущем параграфе. Функция /(г) равна нулю вне дуги (сила трения отсутствует) и единице внутри нее (| г | ^ г0). Заметим, что обычно относительная величина силы трения очень мала (сот) — 106>1. Поэтому в любой момент времени точное решение уравнений (14), (15) лишь на малые величины порядка (ют)-1 отличается от равномерного вращения по ларморовской окружности. Однако характеристики этой окружности: ларморовский радиус г° и положение <е центра Н0 — могут существенно меняться в результате многократного прохождения через дугу.
Будем считать, что дуга представляет собой бесконечный круговой цилиндр, ось которого параллельна внешнему магнитному полю. Последнее предполагается однородным.
Мы будем рассматривать тот случай, когда движение ионов происходит лишь в плоскости поперечного сечения дуги. Тогда задача ока
Зывается двухмерной. Введем систему декартовых координат, ось 0^ которой направлена вдоль магнитного поля, а центр лежит на оси дуги. Введем в рассмотрение однородный центр частицы
* = гч~1£1. (16)
Тогда уравнения движения примут вид
-5-=--<14'>
ТГ = “[УЧ-7аТ1>-/(г>» (15)
Где г определяется из выражения (16).
|
/(cp) sin?, |
![]()
|
Dt |
![]()
Полагая v = vвi9t соответственно, И = Л’- щей скалярной системе уравнений
DX
(V)
DY
TOC o "1-5" h z Dl V,/ 4
Jr=zr&)-/(<?)со«'Р.
Dv
Dt
D<?____ ^
/К, приходим к следую - (17а) (176) (17в) (17г)
|
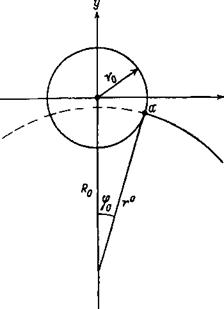
А — траектория ион»; г0 — раднус столб Г° — л»рМОрОВС*ИЙ рЯДКу С; ~ Центр«. |
|
Отсюда следует, что траектория иона представляет собой спираль, Щим с течением времени (17). Оче- Период обращения можно считать 2 Периодическими, так что в (17) [О ?0<сР<2тс — <Ро» = Г 0 ^ ср ^ сро, (18) — ?о < ? < 2тс> |
|
У2_Г2 О |
|
DX |
|
= 0, 1 |
|
Dt |
|
DY Dt ' Dv Dt |
|
Sin?0, |
|
Сот (») те V 1 |
|
T(ь) TZ ‘0’ |
 |
|||
|
|||
|
|||
|
|
||
|
|||
|
|||
|
|||
|
|||
|
|||
 |
|||
Для определения степени приближения осредненных уравнений на интересующем нас интервале изменения энергий и для последующего численного интегрирования перейдем к следующим безразмерным вели-
П
Чинам: Ґ = и>£ (а> = 0.323 • 108 сек.“1), р = —, где а —радиус установки (равный 40 см); V = — , где v0 = u)a^
Тогда после соответствующих преобразований
= (22)
Где а = 0.913 • 10“5; (3* = 45.2; С = ^р=- Р; Ф (х) — интеграл ошибок. Здесь
Использовано выражение для *с: р"(х) * Значения взяты
Из § 1.
В безразмерных переменных уравнения (20), (21) принимают вид
^ = _ 1 (У) агс 5ш (23)
(24)
У(0) = 0.268; К(0)=—0.268; (^ = |К(0)| = 10 см)
° =------- 2УТ ° • р»=°-0808 (г°=3-23 см).
Заметим, что в безразмерных переменных ^г — —1. Поэтому оценку
Применимости осредненных уравнений естественно проводить с помощью величины в = (V*), где V* — минимальное значение скорости иона
В течение рассматриваемого промежутка времени его движения.
Соответствующий интервал энергий 62.5 кэв>£>15 кэв. На нижней его границе (Р1/*)2= = 0.75 и V* ^ 0.13. Величина "™ ■■ (У*)3 ~
— 0.31 дается интерполяцией соответствующей таблицы [5]. Следовательно, е ~ 1.7 • 10“4. Поэтому осредненные уравнения дают решение
С точностью в ~ Ю"4 на интервале времени Д/* — ------ 0.5 • 104 = 5000 [4].
За это время ион проделывает ~800 оборотов по ларморовой окружности. Заметим, что указанная оценка несколько занижена. Если, в частности, определить параметр в по максимальной скорости иона, то окажется, что в ~ 1.1 • 10“4 и — 104, что соответствует 1500 оборотов иона.
Таким образом, следует ожидать удовлетворительного описания движения иона с помощью осредненных уравнений примерно на 1000 оборотов его по ларморовой окружности. Вопрос о достоверности соответствующих выводов в нужном нам интервале энергий сводится к тому — достигнет ли частица за это время соответствующей минимальной скорости или нет. Этот вопрос может быть решен численным интегрированием задачи (23)—(24) на быстродействующих машинах.
Однако уже сейчас можно получить некоторые сведения о процессе замедления ионов.
Прежде всего осредненная система еще нагляднее подчеркивает отмеченные выше закономерности: с течением времени однородный центр подтягивается к дуге (У возрастает), тогда как ларморов радиус
Убывает Далее, кратчайшее расстояние ларморова круга иона
От центра дуги измеряется величиной 7 = — У—V и [как следует из <23)—(24)]
0<5Р = ^1/М1/)[<Р<>—(1 > о > 0), (25)
Следовательно, хотя траектория иона отходит от оси дуги, этот отход происходит значительно медленнее, чем уменьшение ларморова радиуса. Так, например, при уменьшении энергии иона в четыре раза (от 60 до
15 кэв), что соответствует изменению •— от 10 до 5 см, ближайшая
|
£)<'Г |
![]() К оси дуги точка ионной траектории не может сместиться больше, чем на 0.4 см
К оси дуги точка ионной траектории не может сместиться больше, чем на 0.4 см
О Е
Заметим далее, что выражение —^ ■, определяемое в соответствии
С (13) уравнением (21), отличается от выражения (5) множителем ^ =
Учитывающим частичный захват траектории иона силовым полем дуги. Вследствие равномерности движения иона по витку спирали множитель X как Раз и равен отношению времени пребывания иона в дуге к полному периоду обращения.