ЦИКЛОТРОННЫЕ КОЛЕБАНИЯ ПЛАЗМЫ В НЕОДНОРОДНОМ МАГНИТНОМ ПОЛЕ
А. В. Тимофеев
ВВЕДЕНИЕ
Если электромагнитные колебания распространяются в плазме, находящейся в неоднородном магнитном поле, то в какой-то точке (резонансной) их частота ш может стать равной частоте циклотронного вращения заряженных частиц (/ = е, і). При этом возникает ряд характерных явлений, исследование которых является целью настоящего обзора. Оно проводится на примере двух задач, стимулировавших развитие теории циклотронных колебаний. Мы имеем в виду задачу о циклотронном нагреве плазмы с равновесным распределением заряженных частиц по скоростям и задачу об устойчивости неравновесной плазмы в магнитных ловушках.
Циклотронный резонанс создает условия для обмена энергией между колебаниями и вращательной степенью свободы заряженных частиц в магнитном поле. Поэтому, естественно, возникла идея использовать циклотронные колебания для нагрева плазмы ^ 2. Динамика процессов, приводящих к нагреву при циклотронном резонансе в неоднородном магнитном поле, исследовалась в ряде работ 3-8. К настоящему моменту
© «Успехи физических наука», 197.1
1 I 311. т. II), вы і Л
Общую картину явления можно считать выясненной. Для того чтобы наглядно ее представить, полезно использовать пучковую модель плазмы, т. е. считать, что плазма состоит из набора пучков заряженных частиц, движущихся вдоль магнитного поля. Каждый пучок, проходя через резонансную область, модулируется колебаниями,— в нем возбуждаются заряды и токи. Если частота колебаний ш и пучок движется со скоростью V? то пространственный период модуляции будет равен 2лу/(ш — ш/). Отдельные пучки вызывают в плазме колебания, аналогичные известным волнам Ван-Кампена. При непрерывном распределении пучков по скоростям эти колебания с удалением от резонансной точки сдвигаются по фазе и в конце концов затухают под действием интерференции. Поскольку в конечном состоянии видимый порядок в движении частиц отсутствует, в определенном смысле можно утверждать, что энергия колебаний переходит в тепловую. Образование модулированных пучков с их последующей интерференцией, по-видимому, характерно для любых процессов, приводящих к обмену энергией между волной и частицами, если действие этих процессов ограничено малой областью пространства. В приложении с этой точки зрения рассмотрены резонансное черенковское взаимодействие в неоднородной плазме 9, а также взаимодействие, возникающее при резком изменении скорости заряженных частиц 10. Последнее, в частности, приводит к поглощению колебаний, падающих на резкую границу плазмы (см. задачу об аномальном скин-эффекте и). Следует отметить, что при интерференции модулированных пучков информация о фазовых соотношениях сохраняется в скрытом виде, что может привести к явлениям типа эха (см. 9>12, а также8). /
Если распределение заряженных частиц по скоростям термодинамически неравновесно, то при циклотронном резонансе энергия может переходить от плазмы к колебаниям. Неравновесные распределения устанавливаются во многих системах, предназначенных для удержания горячей плазмы. Так, например, в магнитных ловушках удерживаются лишь те частицы, которые движутся под достаточно большим углом к магнитному полю. Частицы, попавшие в так называемый конус ухода, покидают ловушку. В результате распределение частиц по скоростям, поперечным к магнитному полю, обедняется в области малых скоростей.
Возможны два подхода к изучению устойчивости плазмы: нахождение собственных колебаний и исследование эволюции первоначальных возмущений во времени. В первом случае определяется асимптотика возмущения при £ —V оо, во втором — исследуется начальный этап эволюции до установления собственных колебаний. Собственные колебания, как правило, имеют вид стоячих волн, поэтому для их установления необходимо, чтобы в системе существовали точки отражения. В неоднородном магнитном поле колебания при прохождении через резонансную точку не только изменяют свою амплитуду (усиливаются в неравновесной плазме, поглощаются в равновесной), но и частично отражаются (в неравновесной плазме отражение сопровождается усилением, в результате коэффициент отражения может оказаться больше единицы). Поэтому в немонотонном магнитном поле возможны собственные колебания, «запертые» между резонансными точками 13> 14. Эта возможность особенно существенна, если колебания поглощаются на границах плазмы. Однако если колебания отражаются от границ, то дополнительное отражение от резонансных точек можно не учитывать.
Эволюция неустойчивых циклотронных колебаний в неоднородном магнитном поле исследовалась в работе 15. Было показано, что возмущения нарастают конечное время, после чего их амплитуда не меняется, причем оказалось, что отношение конечной амплитуды к начальной равно коэффи-
Циенту усиления колебаний при прохождении через циклотронный резонанс. Возмущения можно считать практически устойчивыми, если коэффициент усиления близок к единице. Интересно отметить, что при диссипативных граничных условиях плазма в этом случае устойчива по отношению к собственным колебаниям. Таким образом, оба подхода к исследованию устойчивости плазмы взаимно дополняют и согласуются друг с другом.
I. РАВНОВЕСНАЯ ПЛАЗМА
1. Динамика резонансного циклотронного взаимодействия, а) Однородное магнитное поле. Рассмотрим движение электрона, находящегося в постоянном однородном магнитном поле и подвергающегося воздействию переменного электрического поля. Предположим, что вектор электрического поля перпендикулярен к магнитному, вращается с той же частотой и в ту же самую сторону, что и электроны в магнитном поле. Из уравнения движения находим
Йу/бй = — (е/те) Е (1.1)
Здесь и — модуль скорости в направлении поперек магнитного поля = Ие (у; Ьи) е~Ше*, величина Е определяется соотношением Е = = Ие (Е; 1Е 0) е~ш, ше = еН/тес — электронная циклотронная
Частота, ш = а)е; используется декартова система координат, ось Ог которой направлена вдоль магнитного поля.
С помощью (1.1) получаем
= —еЕих0 (е2Е21те) (1.2)
Здесь и:е — кинетическая энергия электрона, их0 — начальное значение проекции скорости на Ох. Для совокупности электронов, равномерно распределенных по фазам ларморовского вращения, первое слагаемое в правой части (1.2) исчезает после усреднения. Интересно отметить, что если электрическое поле не поддерживается внешними источниками, то оно будет затухать с декрементом, по порядку величины равным электронной плазменной частоте аре = (4ле2710/те)1'2. Действительно, из (1.2) следует, что за время Ь « а)р* электроны приобретут энергию, сравнимую с энергией поля Е2!8л. При этих оценках предполагается, что электроны распределены равномерно по пространству с плотностью п0.
Б) Циклотронное поглощение в неоднородном магнитном поле. Пусть теперь магнитное поле меняется в продольном направлении Н = Н (г) и электроны движутся вдоль него. В дальнейшем нам понадобится знать не только амплитуду, но и фазу ларморовского вращения. Поэтому введем = их — Для этой величины уравнение движения принимает следующий вид:
Йу_/б& + ше {г (г)) к_ = — (еЕ1те) е~ш. (1.3)
Из (1.3) находим
Г
V - (0 = I £>_ (0) —— [ ехр (— Ш' +
0
TOC o "1-5" h z V *
+ » $ «МО йГ) Л'] ехр (—г | «МОЛ') • (1.4)
О о
Предположим, что циклотронная частота в какой-то точке (резонансной) совпадает с частотой волны. Рассмотрим большие интервалы времени / бшё1, где бо)е — изменение электронной циклотронной частоты на траектории электрона. В этом случае при вычислении интеграла по dt' в (1.4) можно использовать асимптотические методы. Если электрон еще не дошел до резонансной точки t < ts (z (ts) — zs), то асимптотика v_ (t) имеет вид
Мо ~w - (0) exp (_ ,• j Ше (о ^ ~^t)); (1 -5)
О
Здесь учтен только вклад верхнего предела интегрирования (/' = t), так как считается, что электрон успел «позабыть» о моменте включения поля.
При ts следует дополнительно учесть вклад резонансной точки. В ее окрестности электрон находится в фазе с волной, и поэтому подынтегральное выражение в (1.4) при t' = ts имеет точку стационарной фазы 4> *■ 8:
Мо» {р-(°)■~ Т* ехр 1~Шз+* We (z (0) dt'J} х
11 о
X exp [-i j o)e(z (О) dt' J - g. (1-6)
0
Из сопоставления (1.5) и (1.6) следует, что после прохождения резонансной точки амплитуда и фаза циклотронного вращения изменяются. При этом энергия электрона возрастает на величину
6u'e = (тсе2Е2/те) [ук (duyjdz)2]~l.
(Здесь произведено усреднение по начальной фазе ларморовского вращения.) Этот прирост можно получить из следующих соображений.
Электрон, движущийся в неоднородном магнитном поле, пребывает в состоянии резонанса конечное время, которое можно найти из условия | 6Ф | < я/2, где
6Ф=—ш(£ — ts) + ^ dt’(oe(z(t’))
— разность между фазой ларморовского вращения электрона и фазой волны. Подставляя в это выражение о)е (г) = о -(- (г — г3) (й(ое/с?2)^, г — = Уц (г — £„), определяем продолжительность резонансного взаимодействия’ 62 « [2луц (d(лe/dz)г]~^/2. При | Ь — | ■< Ы магнитное поле
Можно считать однородным, поэтому в соответствии с (1.2) оказывается Ьи>е = (е2Е2/2те) (б£)2.
В) Модулированные пучки. Мы показали, что электроны, движущиеся вдоль неоднородного магнитного поля, получают от волны конечное количество энергии. Рассмотрим другое важное следствие, связанное с движением электронов в неоднородном магнитном поле. Предположим, что имеется стационарный и однородный в пространстве поток электронов, движущийся В ПОСТОЯННОЙ скоростью У||. В соответствии с (1.5), (1.6) в резонансной точке скорость ларморовского вращения электронов модулируется электрическим полем. При этом изменение скорости зависит как от начального положения электрона на ларморовский окружности, характеризуемого (0), так и от момента прохождения резонансной точки ts. Предположим, что магнитное поле спадает вдоль оси Ог. В таком поле электроны, прошедшие через резонансную точку, отстают по фазе от электрического поля. Нетрудно понять, что электроны, модуль скорости
Которых изменился на одну и ту же величину, образуют в пространстве спиральную линию (рис. 1 [25])). Она движется вдоль оси z со скоростью Уц и вращается вокруг этой оси с локальной ларморовской частотой. Таким образом, за резонансной точкой появляются электрические токи круговой поляризации. В силу стационарности процесса возбуждаемые ими поля должны иметь частоту первичного
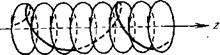 Поля со. Зависимость фазы вторичной волны от координаты z и скорости Уц находим из (1.6):
Поля со. Зависимость фазы вторичной волны от координаты z и скорости Уц находим из (1.6):
Ф (z, Уц) = — [(z — zs)2/2y]|] d(0eldz z.
(1.7) Рис. 1. Модуляция потока электронов
^ в резонансной точке.
ЛеГКО усмотреть СХОДСТВО между ВТО - Жирная линия показывает положение группы
Ричной ВОЛНОЙ И Волнами Ван-Кам - электронов, модуль скорости которых изме -
ТТРНЯ 18 Потлрттнир как ичвргтнп нился на одну и ту же величпну 6v±' Группы
Пена. Последние, как известно, с друГИМ значением би ] образуют аналогич -
ПредСТаВЛЯЮТ колебания, вызываемые ные спирали, сдвинутые по оси z и запол -
Ттупкями чяпяжрттттму чягттттт ттттпт - няющие всю поверхность цилиндра, состав -
Пучками заряженных частиц, ПЛОТ ленного и3 ларморовских окружностей (тон -
Ность которых модулирована в на - кие линии),
Правлении движения. Брамбилле7
Удалось найти асимптотическое решение самосогласованного волнового уравнения циклотронных колебаний, которое можно считать аналогом волны Ван-Кампена.
2. Поле модулированного пучка, а) Адиабатическое волновое уравнение. В предыдущих разделах мы считали электрическое поле колебаний постоянным в пространстве. Действительный интерес представляет задача о резонансном взаимодействии электромагнитных волн. При этом решение должно быть самосогласованным, т. е. следует учитывать, что токи, вызываемые волной, изменяют поле волны.
Будем считать, что магнитное поле меняется с расстоянием по линейному закону dHldz = const <0 и что все электроны движутся с одной и той же постоянной скоростью Уц > 0. При этих условиях волновое уравнение принимает следующий вид:
|
D2E Dz2 |
![]() Е + ‘'ф ] (1.8)
Е + ‘'ф ] (1.8)
Здесь начало координат выбрано в резонансной точке ше (0) = ш.
Не представляет труда установить соответствие между (1.8) и (1.4). Действительно, (1.4) определяет возмущение скорости электрона под действием электрического поля 6у. С возмущением скорости будет связан ток 6/ = —е«обу. Его влияние на колебания и учитывается последним слагаемым в (1.8). В нем, в отличие от (1.4), интегрирование по времени заменено интегрированием по координате на траектории электрона йг'/й<' = У|, начальный момент отнесен в —оо, электрическое поле считается функцией координаты и поэтому оставлено под знаком интегрирования. Если в (1.8) вычислить асимптотику интеграла по dz', считая Е (г') медленно меняющейся функцией и учитывая лишь вклад верхнего предела интегрирования, то получим
DiE/dz'lJr (со2/с2) {1 + [&)ре/ш (сое (г) — со)]} £ = 0; (1.9)
Здесь произведена замена г d(^зe/dz = ае (г) — со.
Уравнение (1.9), часто используемое при анализе циклотронных колебаний в неоднородном магнитном поле, можно получить, описывая движение электронов в колебаниях в гидродинамическом приближении (см., например, 17-19). От волнового уравнения для случая однородного магнитного поля оно отличается лишь тем, что в нем величина поля считается медленно меняющимся параметром. Поэтому (1.9) может быть названо адиабатическим волновым уравнением8. Адиабатическое волновое уравнение является асимптотическим и не учитывает влияния резонансного взаимодействия (вклад точки стационарной фазы в интеграл по dz' при z > 0). Поэтому неудивительно, что в резонансной точке z = 0 оно теряет смысл (имеет особенность). Для продолжения решения через особую точку обычно вводится правило обхода Ландау. А именно, рассматривается аналитическое продолжение (1.9) на плоскость комплексного переменного z и считается, что колебания с Im со = 0 являются пределом нарастающих с Im со > 0. Если Im со > 0, то резонансная (особая) точка zs смещается с действительной оси вниз при dutjdz | Zg < 0 и вверх при (d(oe/dz)Zs >0 (6z = i Im ш [(,d(aeldz)i~1). Соответственно, при (dco,/dz)Zs < 0 особая точка должна обходиться сверху и при dtiijdz |js > 0 снизу. В некоторых работах (см., например, 17-19) указывалось, что для обоснования правила обхода Ландау достаточно учесть электрон-ионные соударения. Действительно, при наличии соударений с частотой v резонансный знаменатель в (1.9) принимает вид 1/(шв (z) —
— со — iv), что эквивалентно переходу к нарастающим колебаниям. За счет столкновений энергия колебаний в окрестности резонансной точки переходит в джоулево тепло. Этот процесс доминирует при V (уц | dmjdz | )1/г (см. ниже). Однако в экспериментальных условиях часто выполняется обратное неравенство. В этом случае обмен энергией между волной и электронами протекает без участия столкновений (см. предыдущие разделы) и, следовательно, обоснование правила обхода Ландау должно быть получено иным способом.
Б) Решение Брамбиллы. Теперь обратимся к волновому уравнению (1.8) которое, разумеется, является регулярным при всех значениях z. Помножим (1.8) на exp [(1/2иц) (dae/dz) z2, продифференцируем результат по dz, после чего помножим на ехр [(—1/2уц) (dutjdz) z2]. Получим
2ip*5Јj> + E’t + * (А - 2p*Q Е = 0; (1.10)
Здесь введены обозначения А = ((0рС/со2) с/уц, р2 = — (1/2уц) (dwjdz) с2/со2, £ = (oz/c. Последнее уравнение отличается от (1.9) дополнительными слагаемыми (третьей и первой производными). Добавление третьей производной устраняет особенность в начале координат (в резонансной точке). При | £ | -+- оо (1.10) имеет решения двух типов: крупно - и мелкомасштабные. Приближенно можно считать, что крупномасштабные решения удовлетворяют адиабатическому уравнению (1.9), в котором отсутствует третья производная. Для мелкомасштабных решений в (1.10) можно опустить два последних слагаемых. При этом находим Е ж С (£) егр2£2; здесь С (£) — медленно меняющаяся функция. Фаза этого решения совпадает с (1.7) и само оно описывает поле модулированного пучка, уходящего от резонансной точки. В соответствии с изложенным в разделе 1, в), такие пучки должны, например, возбуждаться при падении на нее колебаний с большей длиной волны. Изменение пространственного масштаба колебаний принято называть трансформацией. Хорошо известно (см., например, обзор 20), что уравнения с малым параметром перед старшей производной действительно описывают этот эффект. Если скорость электрона и градиент магнитного поля не слишком велики, то в настоящем случае малым параметром является величина 1 /р2.
Для решения (1.10) в работе 7 использовался метод преобразования Лапласа. Получены следующие результаты. Решение, представляющее при z < 0 волну, набегающую на резонансную точку,
Е (0 « |С (1.11)
J-+-CO
При z > 0 имеет вид
•Й/9, -Г Д&/2ЯЖЗ/2) 1/2 оР/2я
Е (0«,уг(Гр/а.) е'л' <и2>
Где Я = no)peL/o)c.
Из (1.12) следует, что крупномасштабные колебания действительно трансформируются в мелкомасштабные. При этом амплитуда крупномасштабных колебаний уменьшается на множитель
Т = е-Р/2, (1.13)
И, следовательно, коэффициент трансформации (доля передаваемой энергии) равен
Т| = 1 — е_Р. (1.14)
Этот результат можно было бы получить, используя упрощенное адиабатическое волновое уравнение (1.9), дополнерное правилом обхода Ландау. Действительно, при £ < 0 возьмем решение в виде Е (£) = _ £-гр/2я git. Продолжим его на область £ > 0, обходя точку £ = 0 в верхней полуплоскости. При этом arg £ получает приращение —л, и соответственно амплитуда Е (£) уменьшается на множитель е~Ы2.
В настоящем рассмотрении не принимались во внимание релятивистские эффекты. В работе 7 показано, что их учет приводит к замене Я + Я [1 - (Уц/с)1.
3. Влияние теплового разброса. Правило обхода Ландау. Теперь предположим, что распределение электронов по продольным скоростям обладает некоторым тепловым разбросом 6уц. В этом случае можно считать, что на резонансную точку набегает совокупность пучков электронов с непрерывно распределенными скоростями. В резонансной точке каждый из этих пучков модулируется колебаниями. В соответствии с (1.7) при удалении от резонанса фазы отдельных пучков сдвигаются. При z —zs ^ уц (6уцйа)е/с? г)-1/2 интерференция полей, связанных с отдельными пучками, приведет к их взаимному уничтожению [26]). Тот же самый результат получился бы при хаотическом распределении фаз отдельных пучков, поэтому в определенном смысле можно утверждать, что упорядоченная энергия колебаний переходит в тепловую. Однако
Фазовая информация сохраняется в скрытом виде и в принципе может
Проявиться в эффектах типа «эха», (см. 9>12).
Чтобы описать явление интерференции количественно, получим выражение для тока, вызываемого волной, за резонансной точкой. Используя (1.6), находим
Б/ (z) = -- епа j ЙУц/ое (У;|) &V я:
Е2П0 р 2Я1 "]t/2 ^ dv|| - ф ^ j
«-STL 15^/aij-J Е(^))-^1оеЫе и +
+ ^—r^E(z). (1.15)
4л и — ше (z) ' ' '
|
В случае максвелловского распределения электронов по скоростям /о. (У||) = (Ш1/^,,) е-«И'*Ч 1>2 интеграл по скоростям в (1.15) легко вычисляется методом перевала: ЛЛ, _ ч / I Лл и-1/6 ) (30!7|| (2 — 2*)) 2/3 |
|
(Ч)2/3 Из (1.16) следует, что характерная длина затухания полей модулирован- Полученные нами выражения справедливы на действительной оси. Уравнением, которое полностью учиты- Поскольку в настоящем рассмотрении мы считаем (dmjdz) Us < 0, это /о Ы =-^7^-exp [ - 2 J, |
|
5* vti о (6V|i I d(aeldz І)1/2. В пределе |
|
"l/іг би’.. |
|
Радиус обхода возрастает, | г — zs биц —V 0 интерференция отсутствует и радиус обхода становится бесконечным. Именно этот случай был рассмотрен в предыдущем разделе. При выполнении условия |
|
Тах |
|
С2 I da>e/dz I |
|
,3/2 |
|
С2 | d(oe/dz |
|
1/2 |
|
(Ьpg (01Л |
|
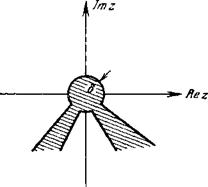
Рис. 2. Плоскость комплексной переменной в окрестности резонансной точки. |
|
Заштрихована область, в которой нельзя использовать упрощенное адиабатическое волновое уравнение (1.9). Распределение электронов по продольным скоростям принимается максвелловским: /0 (г> ц ) = IIII В = (ів її / | ЛшеШ р1^ . |
|
Г in ІТЇ |
|
X exp |
|
-1/3 |
|
X |
|
|
|
|
|
|
|
|
|
|
 |
|
 |
|
Резонансная область расширяется за счет эффекта Допплера. Если изменение циклотронной частоты Да)е в пределах системы достаточно мало,
^^тахр, Ц2/3],
<ое [.с (О с 1 J
То резонансная область перекроет всю систему. В этом случае неоднородность магнитного поля можно вообще не учитывать.
Интересно сопоставить рассматриваемые колебания с электронными лэнгмюровскими колебаниями горячей плазмы. В задаче об электронных лэнгмюровских колебаниях вклад резонансных частиц в выражение для возмущенной функции распределения частиц по скоростям приводил к сингулярности f^(v)~[v—(ш/А:)]-1. Для ее устранения оказалось необходимым учесть нелинейный эффект изменения скорости резонансных частиц под действием поля волны, который приводит к ограничению времени резонансного взаимодействия (см., например, обзор 21). Однако в настоящем случае учет нелинейных эффектов не привел бы к желаемому результату, так как в нерелятивистском пределе частота циклотронного вращения не зависит от энергии. В то же время в неоднородном магнитном поле резонансное условие для отдельного электрона может нарушиться, если он, двигаясь вдоль поля, покинет резонансную зону. Этот эффект и был учтен нами.
|
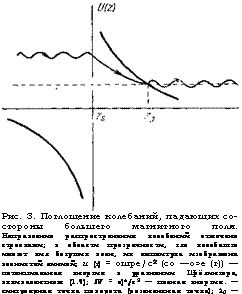
Рис. 3. Поглощение колебаний, падающих со - стороны большего магнитного поля. Направление распространения колебаний отмечено стрелками; в области прозрачности, где колебашгл имеют вид бегущих волн, их амплитуда изображена волнистой линией; и (г) = ошре/с2 (со —о>е (г)) — потенциальная энергия в уравнении Шрёдингера, эквивалентном (1.9); IV = о)*/с2 — полная энергия. — сингулярная точка поворота (резонансная точка); 20 — обычная точка поворота. |
 В обеих задачах при определенных условиях возможно использование сингулярных выражений, дополненных правилом обхода Ландау. Пра рассмотрении электронных лэнгмюровских колебаний такой подход применим, если в начальный момент отсутствовали модулированные пучки (волны Ван-Кампена), и только до тех пор, пока волна не передаст значительную часть своей энергии таким пучкам. В задаче о циклотронных колебаниях адиабатическое волновое уравнение (1.9) применимо в области, свободной от полей, связанных с модулированными пучками.
В обеих задачах при определенных условиях возможно использование сингулярных выражений, дополненных правилом обхода Ландау. Пра рассмотрении электронных лэнгмюровских колебаний такой подход применим, если в начальный момент отсутствовали модулированные пучки (волны Ван-Кампена), и только до тех пор, пока волна не передаст значительную часть своей энергии таким пучкам. В задаче о циклотронных колебаниях адиабатическое волновое уравнение (1.9) применимо в области, свободной от полей, связанных с модулированными пучками.
4. Количественные характеристики резонансного взаимодействия. Будем считать, что распределение электронов по скоростям вдоль магнитного поля имеет тепловой разброс.
В этом случае на достаточном удалении от резонансной точки можно использовать адиабатическое волновое уравнение, дополненное правилом обхода Ландау. Оно имеет вид уравнения Шрёдингера с «потенциалом» Ц (г) = (Ореш/с2 (ш — ше (г)) и «энергией» Ш = ш2/с2 (рис. 3). Из рисунка следует, что области распространения колебаний (области прозрачности) разделены потенциальным барьером. (г5 < 2 < г0). Здесь г0 — обычная точка поворота, в которой обращается в нуль «кинетическая энергия» (Ш = О (г0)), zli — сингулярная точка поворота, в которой «потенциальная энергия» бесконечна.
Рассмотрим колебания, распространяющиеся со стороны больших значений магнитного поля (слева направо). Отношение амплитуды колебаний, прошедших через область непрозрачности, к амплитуде падающей волны дается обычным квантовомеханическим выражением
Го
Т = ехр (г | &ц (г) йг) , (1-17)
Г«
Где
При линейном изменении магнитного ПОЛЯ
0)е (г) = (0 (1 —ТГ2") •
Интеграл в показателе экспоненты легко вычисляется и оказывается равным р/2 (см. (1.13)).
В разделе 3 отмечено, что и при отсутствии теплового разброса для описания длинноволновой части колебаний можно использовать адиабатическое волновое уравнение, дополненное правилом обхода Ландау. Поэтому неудивительно, что вне зависимости от величины разброса коэффициент ослабления длинноволновой части колебаний дается (1.13).
В отличие от задач, рассматриваемых в квантовой механике, в настоящем случае отсутствует отраженная волна (см. 14[27]17, а также42). Поэтому следует считать, что разность между энергиями падающей волны и прошедшей поглощается. В предыдущих разделах было показано, что энергия колебаний тратится на модуляцию потока заряженных частиц, набегающего на резонансную точку. Этот процесс, на первый взгляд, никак не отражен в использованном нами адиабатическом волновом уравнении, и соответствие (1.13) с (1.17) может показаться случайным *). На самом деле это не так. В работе 8, где получено полное волновое уравнение, показано, что взаимодействие между колебаниями и частицами описывается единым аналитическим выражением, которое распадается на адиабатическую и резонансную части лишь асимптотически — на достаточно большом расстоянии от резонансной точки. Однако каждая из этих частей содержит в себе информацию о другой части, поэтому любое изменение процесса резонансного взаимодействия, например под действием ускорения, эффекта Допплера ит. д., отражается на адиабатическом волновом уравнении. Естественно, что и результаты, получаемые из рассмотрения движения отдельных частиц и с помощью адиабатического волнового уравнения, оказываются одинаковыми. Покажем справедливость этого утверждения на простейшем примере плазмы низкой плотности ((а^Ь/юс 1).
Из (1.17) следует, что коэффициент поглощения (доля поглощаемой энергии) при (ореЫ(йс 1 равен
Т) = 1 — Г2 «]ло)р«£/Дос. (1-18)
С другой стороны, количество энергии, поглощаемое электронами, может быть получено с помощью (1.6). Оно равно 6и>е = (тещ/2) 6и |2; здесь 6 и — изменение скорости ларморовского вращения (слагаемое, линейное по 6у, устраняется после усреднения по фазе ларморовского вращения). При низкой плотности электромагнитную энергию модулированных пучков можно не учитывать и поэтому для коэффициента поглощения —
Принять следующее выражение: т| » 6и>в/<5, где 5 = с | Е |2/4л; Е — амплитуда колебаний, падающих на резонансную точку. Простые вычисления приводят к (1.18). В работе ® показано, что и при более высокой ПЛОТНОСТИ, КОГДа ВЫПОЛНЯетСЯ уСЛОВИе С/СйЬ ((0рв/(0)2 с2/(л3>2Ь3/2и^2,
Коэффициент поглощения, получаемый обоими способами, оказывается одним и тем же (т| « 1).
Адиабатическое волновое уравнение в виде (1.9), вообще говоря, справедливо, только если магнитное поле меняется по линейному закону, не учитывается эффект Допплера и ускорение частиц в неоднородном магнитном поле. В работе 8 эквивалентность обоих подходов была проверена на вычислении соответствующих поправок к коэффициенту поглощения (1.18) [28]):
|
|
|
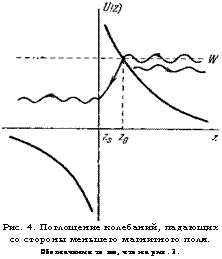
Рис. 4. Поглощение колебаний, падающих со стороны меньшего магнитного поля. Обозначения те же, что на рис. 3. |
 Здесь первое слагаемое учитывает совместное действие эффекта Допплера и ускорения частиц в неоднородном магнитном поле, второе — связано с нелинейным характером изменения магнитного поля, угловые скобки означают усреднение по скоростям; плотность плазмы считается низкой (Р = со^Ь/сос < 1).
Здесь первое слагаемое учитывает совместное действие эффекта Допплера и ускорения частиц в неоднородном магнитном поле, второе — связано с нелинейным характером изменения магнитного поля, угловые скобки означают усреднение по скоростям; плотность плазмы считается низкой (Р = со^Ь/сос < 1).
До сих пор мы рассматривали циклотронные колебания, падающие на резонансную точку со стороны больших значений магнитного поля.
Ниже мы увидим, что колебания, распространяющиеся в обратном направлении, слабее взаимодействуют с плазмой и поэтому представляют меньший интерес. Из рис. 4 следует, что такие колебания попадают сначала на обычную точку поворота, от которой частично отражаются. Отраженная волна может быть найдена в квазиклассическом приближении методом Цваана (см. 14) или при линейном профиле магнитного поля с помощью точного решения уравнения (1.9), выражающегося через функции Уиттекера 14- 17. Вычисления приводят к следующим результатам:
Е = I Я I2 = (1 — Е-*)2, (1.20)
Л = 1 - | Я |2 - | т I2 = е-» (1 - е-0); (1.21)
Го
Здесь, как и ранее, р = 2£ | (при линейном профиле магнитного
Г«
Поля Р = ясйр,>/у/сос, Я — отношение амплитуды отраженной волны к падающей; коэффициент ослабления Т не зависит от направления распространения колебаний и дается (1.13), (1.17). Напомним, что для колебаний, падающих со стороны большего магнитного поля, коэффициент отражения равен нулю.
При Р <С 1 (низкая плотность, большие градиенты магнитного поля) плазма практически одинаково взаимодействует с колебаниями, падающими на точку циклотронного резонанса с противоположных сторон. В этом случае с точностью до величин порядка р имеем | « 0, т) « р. В то же время при р 1 колебания, падающие со стороны большего магнитного поля, почти целиком поглощаются, а со стороны меньшего — отражаются. Следовательно, при Р З5 1 для эффективной передачи энергии плазме необходимо, чтобы между излучателем и резонансной точкой магнитное поле уменьшалось х. Эта область была названа магнитным берегом «по аналогии с диссипацией волн, набегающих на наклонный берег океана» ь.
Нагрев ионов в установке с магнитным берегом был осуществлен в работе 2 [29]). В дальнейшем этот метод развивался в работах 22- 23 и др. Циклотронные колебания использовались также для нагрева электронной компоненты плазмы (см., например, 24), причем нередко осуществлялся режим электронного циклотронного резонанса, т. е. энергия, необходимая для ионизации газа, поставлялась циклотронными колебаниями. Нам не известны экспериментальные работы, посвященные проверке характерных зависимостей, полученных в теории, например, зависимости коэффициента поглощения от плотности плазмы и градиента магнитного поля. Это объясняется, по-видимому, трудностями вариации параметров в реальных системах. В то же время отметим, что в работе 6 в соответствии с (1.13) наблюдалось почти полное поглощение колебаний при достаточно большой плотности плазмы.
В работе 26 предложено использовать циклотронные колебания для «затыкания пробок» в магнитных ловушках. Дело в том, что в магнитных ловушках не удерживаются частицы, скорость которых направлена под достаточно малым углом к аксиальному магнитному полю, т. е. попадает в так называемый конус ухода. Предполагалось, что если расположить точки циклотронного резонанса в магнитных пробках, то частицы, покидающие ловушку, за счет циклотронного поглощения будут увеличивать поперечную компоненту скорости. При этом вектор скорости повернется, и уходящие частицы перейдут в число удерживаемых. Однако в 2,1 бьп. о показано (см. также 27), что основным результатом резонансного циклотронного взаимодействия является усиленная диффузия функции распределения заряженных частиц по поперечным скоростям. Диффузия должна приводить к заполнению конуса ухода, а следовательно, и к возрастанию потерь частиц. Действительно, из (1.6) следует, что изменение поперечной компоненты скорости зависит от соотношения между фазой ларморовского вращения частиц и фазой поля в момент прохождения циклотронного резонанса. Если частицы распределены равномерно на ларморовских окружностях, то в первом приближении по амплитуде поля энергия ларморовского вращения может с равной вероятностью как увеличиваться, так и уменьшаться. Систематическое поглощение энергии является более слабым квадратичным эффектом по полю волны.