Содержание
****JavaScript based drop down DHTML menu generated by NavStudio. (OpenCube Inc. - http://www.opencube.com)****
Печать
Экономия чернил
Упаковочное оборудование Глава V.
ПРОЕКТИРОВАНИЕ МЕХАНИЗМОВ УПАКОВОЧНЫХ АВТОМАТОВ
 Рычажно-зубчатые механизмы
Рычажно-зубчатые механизмы
Рычажно-зубчатые механизмы
Кинематика
Рычажно-зубчатый механизм, в котором ведомое звено совершает периодическое движение с мгновенной остановкой, можно выполнить по схеме, изображенной на рис. 97. Этот механизм состоит из ведущего кривошипа а, шатуна b, коромысла c, неподвижного звена (стойки) d и трех зубчатых колес a, e и f, из которых колеса a и f равных размеров.

Рис. 97. Рычажно-зубчатый механизм.
Колесо a жестко соединено с кривошипом a, колесо e свободно вращается на валике B звена b, колесо f жестко закреплено на валу C и представляет собой ведомое звено механизма. Введем следующие обозначения (рис. 97):
а, b, c, d – длины звеньев шарнирного четырехзвенника OABC;
ra, re, rf – радиусы начальных окружностей зубчатых колес a, e и f;
 – углы между соседними звеньями шарнирного четырехзвенника ОАВС;
– углы между соседними звеньями шарнирного четырехзвенника ОАВС;
 – угол поворота колеса f;
– угол поворота колеса f;
 – угол между продолжениями направлений шатуна b и стойки d;
– угол между продолжениями направлений шатуна b и стойки d;
 – угловая скорость ведущего кривошипа а;
– угловая скорость ведущего кривошипа а;
 – угловая скорость ведомого колеса f;
– угловая скорость ведомого колеса f;
p – длина диагонали АС.
Повернем кривошип ОА (рис. 98) из положения OA1, характеризуемого углом  , в положение OA2, характеризуемое углом
, в положение OA2, характеризуемое углом  . Тогда шатун АВ перейдет из положения А1В1 в положение А2В2 и коромысло CB из положения CB1 – в положение CB2. На чертеже показаны углы между соседними звеньями четырехзвенника в двух рассматриваемых его положениях –
. Тогда шатун АВ перейдет из положения А1В1 в положение А2В2 и коромысло CB из положения CB1 – в положение CB2. На чертеже показаны углы между соседними звеньями четырехзвенника в двух рассматриваемых его положениях –  и
и  ,
,  и
и  ,
,  и
и  .
.

Рис. 98. Определение угла поворота ведомого звена рычажно-зубчатого механизма.
Для определения угла поворота колеса f, соответствующего углу поворота кривошипа ОА из положения OA1 в положение OA2, т.е. углу (  ), отбросим мысленно шарнир O и переместим механизм из положения OA2B2C, сохраняя углы
), отбросим мысленно шарнир O и переместим механизм из положения OA2B2C, сохраняя углы  и
и  , в положение O’A’B1C. Для этого поворачиваем механизм вокруг центра C до тех пор, пока звено СВ2 не перейдет в положение CB1. Колесо e при таком перемещении не будет вращаться относительно своей оси. Колесо f за счет зацепления с колесом e повернется назад на угол (
, в положение O’A’B1C. Для этого поворачиваем механизм вокруг центра C до тех пор, пока звено СВ2 не перейдет в положение CB1. Колесо e при таком перемещении не будет вращаться относительно своей оси. Колесо f за счет зацепления с колесом e повернется назад на угол (  ).
).
Сохраняя угол 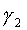 , повернем вокруг центра В1 звенья O’A’B1 в положение O’’A1B1, с тем, чтобы шатун А’B1 совпал А1B1. Тогда колесо e повернется вокруг своей оси на угол (
, повернем вокруг центра В1 звенья O’A’B1 в положение O’’A1B1, с тем, чтобы шатун А’B1 совпал А1B1. Тогда колесо e повернется вокруг своей оси на угол ( 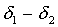 ), а находящееся с ним в зацеплении колесо f с учетом соотношения радиусов колес повернется назад, на угол
), а находящееся с ним в зацеплении колесо f с учетом соотношения радиусов колес повернется назад, на угол  . Наконец, повернем вокруг центра A1 кривошип из положения A1O’’ в первоначальное положение A1O, т.е. соответственно назад на угол (
. Наконец, повернем вокруг центра A1 кривошип из положения A1O’’ в первоначальное положение A1O, т.е. соответственно назад на угол ( 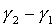 ). При этом колесо f повернется на такой же угол, поскольку радиусы колес a и f между собой равны.
). При этом колесо f повернется на такой же угол, поскольку радиусы колес a и f между собой равны.
За счет этих трех частичных вращений колесо f попадет в положение, характеризуемое углом поворота 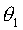 . Отсюда угол поворота колеса f, соответствующий углу поворота кривошипа (а2 – a1), будет равен
. Отсюда угол поворота колеса f, соответствующий углу поворота кривошипа (а2 – a1), будет равен
(133)
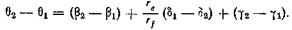
Для бесконечно малого поворота
(134)
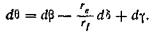
При этом следует иметь в виду, что  отрицательно, если
отрицательно, если 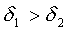 .
.
Отношение угловых скоростей ведомого и ведущего звеньев рычажно-зубчатого механизма.
(135)
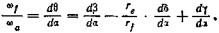
Из рис. 97
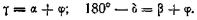
Дифференцируя, получим

Подставляем значения 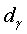 и
и 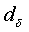 в формулу (135)
в формулу (135)
(136)
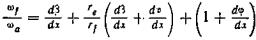
или
(137)
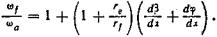
Так как
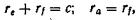
то
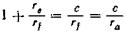
и
(138)
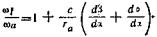
Учитывая, что при равенстве размеров колес a и f равны также длины шатуна b и коромысла c, из равнобедренного треугольника: АВС (рис. 97) найдем
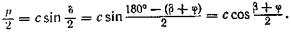
Отсюда
(139)
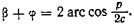
Дифференцируя выражение (139) по переменной 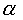 , получим
, получим
(140)
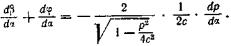
Из треугольника ОАС (рис. 97)
(141)
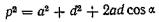
Дифференцируя выражение (141) по переменной а, получим
(142)
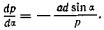
Подставляя это значение  в выражение (140), найдем
в выражение (140), найдем
(143)

и соответственно из выражения (138) получим
(144)
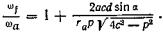
На рис. 99 по уравнению (144) построена кривая I при следующих данных:
a = 15; c = 35; d = 50; ra = 25.
Для того, чтобы максимумы кривой I совпадали с значениями 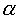 = 90° и
= 90° и 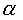 = 270°, необходимо, чтобы при этих значениях угла
= 270°, необходимо, чтобы при этих значениях угла 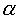 величина производной
величина производной 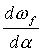 была равна нулю.
была равна нулю.
Дифференцируя уравнение (144) и приравнивая производную 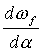 нулю, получим
нулю, получим
(145)
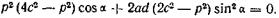
При 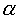 = 90° и
= 90° и 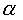 = 270° из выражений (141) и (145) найдем
= 270° из выражений (141) и (145) найдем
(146)
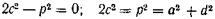
и
(147)
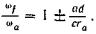
Знак плюс соответствует углу 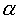 = 90°, знак минус углу
= 90°, знак минус углу  = 270°.
= 270°.
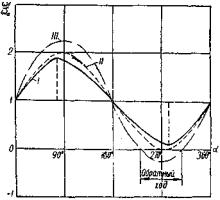
Рис. 99. Графики изменения отношения угловых скоростей ведомого и ведущего звеньев рычажно-зубчатого механизма.
Чтобы при угле 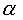 = 270° имела место мгновенная остановка движения колеса f, необходимо получить
= 270° имела место мгновенная остановка движения колеса f, необходимо получить
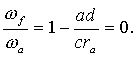
Отсюда в рассматриваемом механизме должно быть такое соотношение размеров звеньев:
(148)
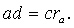
При этом соотношении размеров звеньев из уравнения (147) получим, что при 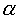 = 90° величина
= 90° величина 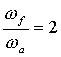 , а при
, а при 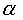 = 270°
= 270° 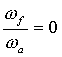 .
.
Кривая II на рис. 99 показывает изменение величины 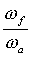 за один полный оборот кривошипа a в этом случае.
за один полный оборот кривошипа a в этом случае.
Как показывает исследование, за один полный оборот кривошипа а колесо f при ad < cra совершает периодическое движение в одном направлении (кривая I на рис. 99), а при ad > cra – реверсивное движение (кривая III на рис. 99). Методы расчета размеров звеньев таких механизмов разработаны.
Выбор основных размеров механизма
Из соотношений (146) и (148), если задаться двумя величинами, например, с и rа, можно найти остальные две необходимые величины d и а.
Величиной rа задаются так, чтобы получить зубчатое колесо без подреза зубьев и требуемого по прочности модуля. Величину re выбирают равной или большей величины ra. Тогда (рис. 97)
(149)
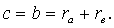
Умножив уравнение (148) почленно на два и сложив его также почленно с уравнением (146), получим
(150)
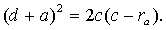
Отсюда
(151)
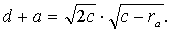
Аналогично
(152)
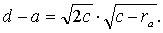
Складывая и вычитая уравнения (151) и (152), окончательно определяем
(153)
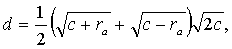
(154)
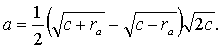
Пример расчета размеров механизма
Принимаем число зубьев колеса а rа – 20; модуль зацепления m = 2,5 мм.
Тогда
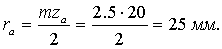
Принимаем re = rа = 25 мм.
Тогда по формуле (149)
с = 50 мм.
Из формул (153) и (154)
d = 68,3 мм, a = 18,3 мм.
CSS Menu by OpenCube


 . Наконец, повернем вокруг центра A1 кривошип из положения A1O’’ в первоначальное положение A1O, т.е. соответственно назад на угол (
. Наконец, повернем вокруг центра A1 кривошип из положения A1O’’ в первоначальное положение A1O, т.е. соответственно назад на угол ( 
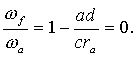
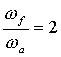 , а при
, а при 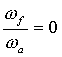 .
.