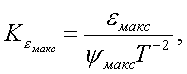
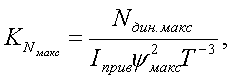


Вид обработки | Точность (в мм) | |
экономическая | достижимая | |
Ручная опиловка и доводка по шаблону | ±0,1 | ±0,03 |
Опиловка на станке при тех же условиях | ±0,05 | ±0,02 |
Строгание и долбление по разметке | ±1,0 | ±0,2 |
Фрезерование по разметке | ±1,5 | ±0,8 |
Фрезерование по копиру на станках с механическим управлением | ±0,2 | ±0,08 |
То же, на станках со следящей системой | ±0,05 | ±0,01 |
Обтачивание по копиру | ±0,2 | ±0,05 |
Шлифование на станках с пантографом | ±0,02 | ±0,01 |

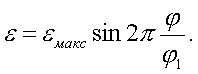
Законы движения | |||
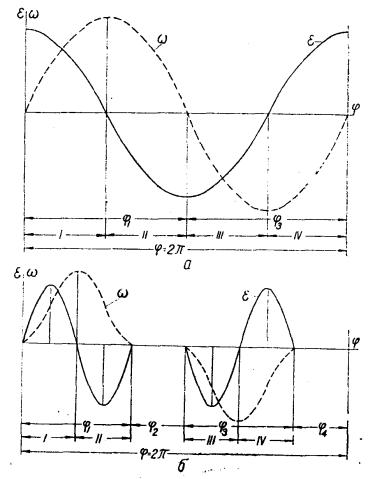
Косинусоидальный | 1,57 | 4,94 | 3,88 |
Синусоидальный | 2,00 | 6,28 | 8,15 |
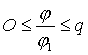

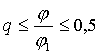
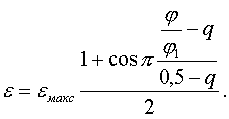
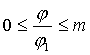
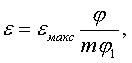

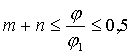
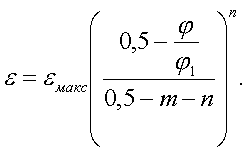
Законы движения | Значения | ||||||
q | m | n | u | ||||
С диаграммой ускорений из двух ветвей сопряженных гармоник | 0,030,05 | –– | –– | –– | 1,461,49 | 5,765,81 | 4,044,26 |
С диаграммой ускорений, очерченной трапецией и вогнутой параболой степени u | ––– | 0,030,030,03 | 0,070,120,12 | 1,501,501,75 | 1,471,551,47 | 6,005,085,61 | 3,954,784,38 |
Законы движения | Значения | ||||
m | n | ||||
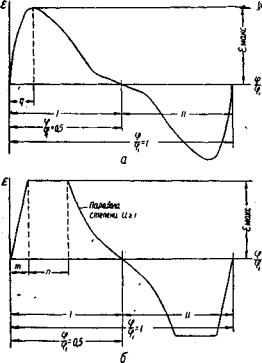
Трапецеидальный (неравнобокая трапеция) | 0,05 | 0,10 | 1,62 | 5,40 | 4,40 |
0,05 | 0,20 | 1,71 | 4,88 | 5,46 | |
0,05 | 0,30 | 1,83 | 4,57 | 6,80 | |
Трапецеидальный (разнобокая трапеция) | 0,05 | 0,40 | 2,00 | 4,44 | 8,40 |
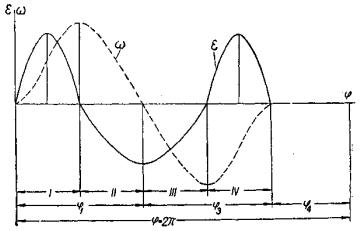

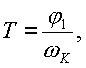
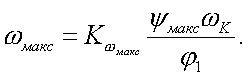
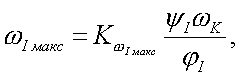

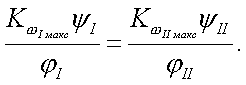
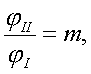

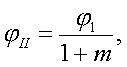

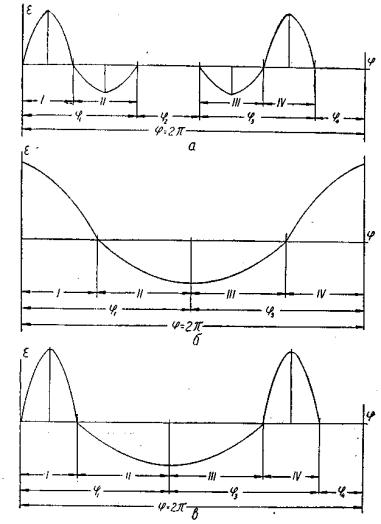
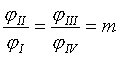 принимаются в этом случае равными от 1,5 до 2,5. Наивыгоднейшее значение этого соотношения можно найти путем подсчета суммарных нагрузок от сил инерции и сил воздействия пружины.
принимаются в этом случае равными от 1,5 до 2,5. Наивыгоднейшее значение этого соотношения можно найти путем подсчета суммарных нагрузок от сил инерции и сил воздействия пружины. 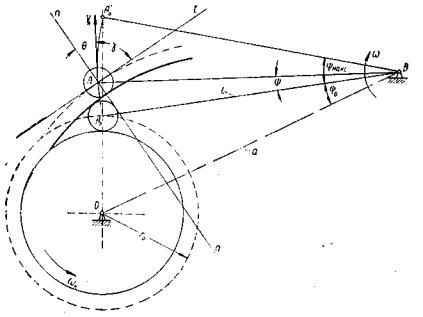
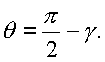
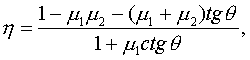
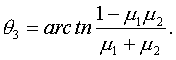
Материал трущихся поверхностей | Коэффициент трения скольжения | |
при хорошейсмазке | при недостаточной смазке | |
Сталь по сталиСталь по чугунуСталь по бронзе | 0,05–0,100,05–0,150,10–0,15 | 0,150,180,15 |