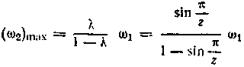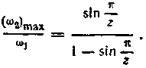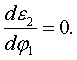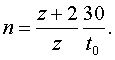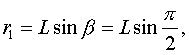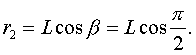Мальтийские механизмы Кинематика Мальтийский механизм, расчетная схема которого дана на рис. 96, состоит из вращающегося с постоянной угловой скоростью водила 1 и неравномерно вращающегося с периодическими остановками мальтийского креста 2. Введем следующие обозначения: z – число пазов мальтийского креста;  – текущий угол поворота водила;  – текущий угол поворота креста; r1 – радиус водила; r2 – радиус креста; L – межцентровое расстояние;  – половина угла между смежными пазами креста;  – угол поворота водила, соответствующий повороту креста на угол  ; Т – время полного оборота водила; t0 – время остановки движения креста; n – число оборотов водила и минуту;  – отношение  .  Рис. 96. Расчетная схема мальтийского механизма. Остановка движения креста имеет место во время поворота водила на угол  . Соответственно (115)  Для того, чтобы в начале и в конце поворота креста не было жестких ударов, вектор скорости точки А0 водила должен быть направлен вдоль паза креста в этих крайних положениях. Отсюда (116)  В зависимости от числа пазов креста угол  можно определить из следующего соотношения: (117)  С учетом соотношений (116) и (117) (118)  (119)  Так как время полного оборота водила (120)  то окончательно время остановки креста (121)  Для определения угловой скорости вращения мальтийского креста рассмотрим прямоугольные треугольники O2BA и O1BA. Из треугольника O2BA (122)  Разделив числитель и знаменатель выражения (122) на L, получим: (123)  (124)  Угловая скорость вращения креста (125)  где угловая скорость водила (126)  Угловое ускорение вращения креста (127)  Исследуем, при каких условиях величины угловой скорости  и углового ускорения  имеют минимальные и максимальные значения. Угловая скорость креста  = 0 при  т. е. при  или при  В этом положении механизма угловое ускорение креста  т. е. в начале и в конце поворота креста имеет место мягкий удар (зависящий от мгновенного возникновения ускорения). Так как при z = | 3 | 4 | 5 | 6 | 8 |  | 1,73 | 1 | 0,73 | 0,58 | 0,41 |
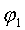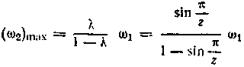
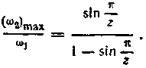
то величина мягкого удара будет тем меньше, чем больше число пазов креста и чем меньше угловая скорость водила. Угловое ускорение креста z2 = 0 при  = 0, т.е. в середине поворота креста. Угловая скорость креста в этом положении достигает максимального значения  и  Так как при z = | 3 | 4 | 5 | 6 | 8 | 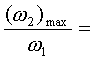 | 6,46 | 2,41 | 1,43 | 1 | 0,62 |
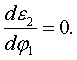
то величина максимальной угловой скорости креста также будет тем меньше, чем больше число пазов креста и чем меньше угловая скорость водила. Положение механизма, при котором угловое ускорение креста достигает максимального значения, можно найти из уравнения  Решение этого уравнения приводит к следующим результатам. При z = | 3 | 4 | 5 | 6 | 8 | 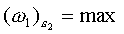 | 4°46’ | 11°28’ | 17°34’ | 22°54’ | 31°39’ | 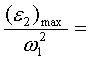 | 31,4 | 5,4 | 2,3 | 1,3 | 0,7 |
Эти результаты показывают нецелесообразность применения мальтийских механизмов с малым числом пазов креста. Выбор основных размеров механизма Если число остановок креста, требующихся по технологическому процессу, обозначим а, число холостых остановок, т. е. таких, которые не требуются по технологическому процессу, но неизбежны при конструктивной компоновке механизма, обозначим b, то число пазов (128) z = a + b. 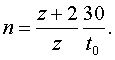Задаваясь временем, необходимым для совершения наиболее длительной операции – t0, из уравнения (121), получим необходимое число оборотов водила в минуту (129)  Принятое ранее условие отсутствия жестких ударов в начале и в конце поворота креста определяет соотношения для выбора геометрических размеров механизма. 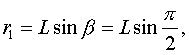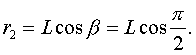Из прямоугольного треугольника O1A0O2 (130)  (131)  Задаваясь величиной L, можно определить r1 и r2, а задаваясь величиной r1 или r2, из треугольника O1A0O2 можно определить остальные два геометрических размера. 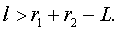Длина паза (132)  Пример расчета размеров механизма Из технологических и конструктивных соображений, принято t0 = 0,5 сек; z = 8; L = 400 мм. По формуле (129) число оборотов водила в минуту n = 75. По формулам (130) и (131) радиусы водила и креста r1 = 153,1 мм, r2 = 369,6 мм. Длина паза l > 122,7 мм. С учетом размещения ролика водила принимаем l = 170 мм. |
Содержание
Выбор кинематических схем для механизмов
Кинематика