Изменение структуры гранул во время полета
Формирование структуры гранул из капель расплава во время их полета в башне является следствием процессов нестационарного теплообмена, осложненного действием внутреннего источника тепла в виде теплоты кристаллизации.
Задачей инженерного расчета обычно является определение высоты грануляционной башни или времени падения гранулы, в течение которого она затвердеет настолько, что уже не деформируется при попадании на коническое днище башни или в плотную фазу кипящего слоя.
Ввиду того, что прочность гранулы по мере ее охлаждения (кристаллизации) непрерывно растет, важно установить такую температуру, при которой соотношение кристаллов вещества и жидкой фазы обеспечивает необходимую твердость структуре гранулы.
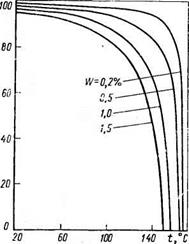 Степень кристаллизации плава в грануле можно определить по равновесным кривым содержания вещества, выделившегося в виде кристаллов и находящегося еще в жидкой фазе (плав + + вода). Такие кривые для аммиачной селитры при содержании влаги в исходном плаве 1,5; 1,0; 0,5 и 0,2% приведены на рис. 5.5 [110]. Из рисунка видно, что даже небольшое содержание влаги в исходном плаве приводит к тому, что значительная доля вещества в гранулах находится в виде жидкой фазы при температурах меньших начальной температуры кристаллизации — вследствие высокой растворимости нитрата аммония.
Степень кристаллизации плава в грануле можно определить по равновесным кривым содержания вещества, выделившегося в виде кристаллов и находящегося еще в жидкой фазе (плав + + вода). Такие кривые для аммиачной селитры при содержании влаги в исходном плаве 1,5; 1,0; 0,5 и 0,2% приведены на рис. 5.5 [110]. Из рисунка видно, что даже небольшое содержание влаги в исходном плаве приводит к тому, что значительная доля вещества в гранулах находится в виде жидкой фазы при температурах меньших начальной температуры кристаллизации — вследствие высокой растворимости нитрата аммония.
Решить вопрос о том, какая степень кристаллизации соответствует необходимой прочности структуры гранулы, очевидно, можно лишь опытным путем. По - мимо равновесных соотношений
Рис. 5.5. Зависимость содержания
H4N03 В кристаллах X охлаждаемой
гранулы от температуры / при различном
содержании влаги W в плаве
|
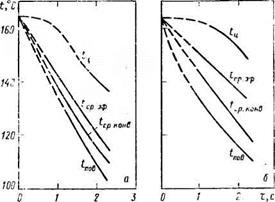
Рис. 5.6. Изменение температуры поверхности 1ПОв, центра /ц, средней конвективной /ср. ионв и средней эффективной ^ср. эф при охлаждении гранул, падающих в башне с высоты Н: а—dr—2 .мм; б — dr—3 мм |
прочность структуры гранул определяется также прочностью межкристаллических связей, обусловленных кинетикой кристаллизации и интенсивностью теплообмена между гранулой и охлаждающим агентом.
В работе [ПО] приводятся результаты приближенного теплового расчета процесса гранулообразования, выполненного на базе известных решений задач нестационарной теплопроводности сферического тела с внутренним источником тепла в условиях интенсивного конвективного теплоотвода [91].
На рис. 5.6 изображены расчетные кривые изменения температуры на поверхности гранулы /,шв, в центре гранулы t^, средней эффективной температуры гранулы <ср. эф и средней температуры гранул /ср. коив без учета внутреннего термического со противления.
■ Охлаждение гранул в современных грануляционных башнях завершается, как правило, в псевдоожиженном слое, расположенном в нижней части башни [ПО].
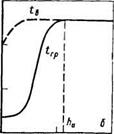
Теплообмен между твердыми частицами и газом в псевдоожиженном слое характеризуется следующими особенностями: температура твердых частиц (гранул) tTV практически постоянна в объеме всего псевдоожиженного слоя;
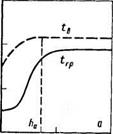
температура охлаждающего агента (воздуха) tB изменяется на активном участке Аа (вблизи газораспределительной решетки) и практически постоянна в остальном объеме слоя (рис. 5.7).
Перенос тепла (охлаждение) в псевдоожиженном слое складывается из следующих стадий [92]:
отвод тепла из системы с потоком ожижающего агента;
trp, t6:c
 50 40
50 40
ЗО 20
О 10 20 О W И, мм
Рис. 5.7. Изменение температур по высоте Н псевдоожиженного слоя (по дан-
ным Е. А. Казаковой) при различной скорости воздуха (сплошные линии —
температура гранул /; штриховые линии — температура воздуха ts):
а — w= 1,4 м/с; б — w= 1,1 м/с
перенос тепла от поверхности твердых частиц (гранул) к потоку ожижающего агента;
распределение теплового потока внутри гранулы.
Признаком эффективного отвода тепла из псевдоожиженной системы твердых частиц является равенство температуры гранул и воздуха на выходе из слоя. Это равенство обеспечивается при достаточной высоте псевдоожиженного слоя, когда Ясл>/іа, а также при условии равномерного распределения ожижающего агента в объеме слоя и полном перемешивании твердой фазы. При этом высоту активной зоны теплообмена можно рассчитать из теплового баланса по формуле
ha = 0,36 -10іw pcRtI<x (1 — е), (5.20)
где с — теплоемкость среды; /?т — радиус частицы; е — порозиость слоя.
Величина /га, рассчитанная по уравнению (5.20) для гранул аммиачной селитры d—2 мм при w = 2 м/с, составляет ~0,02м.
В реальных условиях, как показывает опыт эксплуатации промышленных аппаратов [ПО], практически невозможно создать равномерный псевдоожиженный слой малой высоты — вследствие неравномерности распределения ожижающего агента по сечению газораспределительной решетки.
Высота псевдоожиженного слоя в промышленных аппаратах обычно составляет «0,1 м, отвод тепла в этом случае осуществляется практически полностью: температура гранул
и воздуха на выходе из основного объема слоя почти совпадают. Это утверждение, однако, справедливо преимущественно для аппаратов цилиндрической формы при условии полного перемешивания твердых частиц. Применение аппаратов прямоугольного сечения или лотковой формы для охлаждения гранул в псевдоожиженном слое приводит порой к тому, что tB>t или tCtB, в зависимости от степени завершенности теплообмена
в условиях перемешивания твердой фазы, близких к вытеснению.
Теплообмен между твердыми частицами и ожижающим агентом зависит от теплопроводности пленки газа, окружающего частицу (ост) и конвекции (аКонв)- Составляющей теплообмена, определяемой излучением (ссизл) в низкотемпературных псевдоожиженных системах обычно пренебрегают вследствие ее малости.
В экспериментальных исследованиях обычно получают а как результат совместного действия ат и аКОнв-
Отвод тепла теплопроводностью от сферической гранулы через шарообразную газовую пленку может быть выражен следующим уравнением:
![]() а,=2ХД/т(1 —dT/do),
а,=2ХД/т(1 —dT/do),
где d0—диаметр газовой пленки, окружающей частицу; dT — диаметр гранулы; X — коэффициент теплопроводности среды (воздуха).
Для одиночной частицы d0—>00, ат—*-2X/dT, a Nu = aTdT/'k—>-
—>2.
В работе [96] уравнение (5.20) применено к псевдоожиженному слою с учетом условия dr/d0>l/2.
Анализ обширных экспериментальных данных позволяет рекомендовать следующие зависимости для расчета теплообмена при охлаждении гранул в псевдоожиженном слое [34]:
![]() при 5«Re<70 Nu=0,021Re1-", при 70<Re<200 Nu = 0,38Re°-8, при 60<Re<500 Nu = 0,3l6Re°'8.
при 5«Re<70 Nu=0,021Re1-", при 70<Re<200 Nu = 0,38Re°-8, при 60<Re<500 Nu = 0,3l6Re°'8.
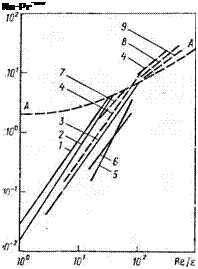
Представляет интерес сопоставление интенсивности теплообмена в зависимости от Re/є для одиночной частицы, неподвижного и псевдоожиженного слоев. Сравнение, выполненное ранее [79] и дополненное в работе [110], представлено на рис. 5.8. Из приведенного на рис. 5.8 сопоставления следует, что в области Re/eClOO интенсивность теплообмена в неподвижном и псевдоожиженном слоях ниже, чем для одиночной сферической частицы (кривая А—А). Объяснение этому явлению авторы работы [96] видят в неравномерности распределения скорости ожижающего агента, обтекающего частицы, вследствие чего при малой скорости существует вероятность агрегирования частиц, и их поверхность не полностью участвует в теплообмене. С увеличением скорости ожижающего агента равномерность обтекания частиц газовым потоком возрастает, происходит обнажение всей поверхности частиц, и интенсивность теплообмена в таком псевдоожиженном слое становится равной интенсивности теплообмена при обтекании одиночной частицы. При Re/e>100 происходит турбулизация газовой пленки, окружающей частицу, и интенсивность теплообмена при этом превышает значения, характерные для обтекания одиночной частицы. В этой области и осуществляется большинство процессов
охлаждения гранулированных продуктов, в частности охлаждение минеральных удобрений.
Различия, существующие в известных выражениях, обобщающих результаты экспериментальных исследований по теплообмену в псевдоожиженных системах, таковы, что они не позволяют рекомендовать единой корреляции, описывающей данные разных авторов.
Предложенную в работе [96] для Re/e>200 формулу
Nu=0,4(Re/e)2/3Pr1/3 (5.25)
■сами авторы рассматривают как весьма ориентировочную: с некоторыми опытными данными она расходится на ±100—200%.
Математическое описание процесса переноса тепла в условиях внутренней задачи, касающейся распределения теплового потока внутри гранулы, разработано достаточно подробно [91].
Для расчета узлов грануляционной башни задаются производительностью, размером гранул drp, типом и количеством распыливающих устройств (грануляторов). В зависимости от этого по экспериментальным данным подбирают среднюю плотность орошения башни qoP, которая и определяет площадь ее орошения. Обычно qDp для центробежных разбрызгивателей составляет 300,для статических — 500—600кг/(м2-ч). Диаметр башни принимают с запасом 0,7—1 м. •
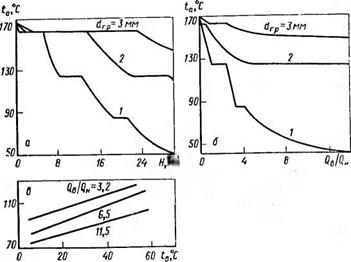
Высоту башни определяют из рис. 5.9 по заданному размеру гранул и их адиабатической температуре, которая в нижней части башни зависит от высоты полета и размера гранул, температуры воздуха, соотношения расходов воздуха и плава, обычно для летних условий принимаемого равным 9—10. Эти
 зависимости, рассчитанные на ЭВМ для аммиачной селитры, приведены на рис. 5.9.
зависимости, рассчитанные на ЭВМ для аммиачной селитры, приведены на рис. 5.9.
Задаваясь, в зависимости от конструкции, числом грануляторов на одной башне, определяют их производительность и конструктивные параметры. Диаметр отверстий dB опреде-
Рис. 5.8. Сопоставление данных различных авторов [21] по теплообмену между частицами и средой в неподвижном и псевдоожиженном слоях:
/ — Рихардсона; 2 — Казаковой; 3 — Франца; 4 — Линдина; 5 — Синкори; 6 — Казаковой и Линдина; 7 — Хертнса; 8 — Васано - вой; 9— Вахрушева; сплошные линии =— измерение температуры среды незащищенной термопарой, штриховые — защищенной; А—А — теплообмен для одиночной закрепленной частицы
|
Рис. 5.9. Зависимость адиабатической температуры ts гранул аммиачной селитры диаметром t/гр от различных параметров процесса: а — от высоты И полета гранул в башне при температуре охлаждающего воздуха Дв=> =30 “С, QB/C„=9, о0=6 м/с; 6 — от соотношения расходов охлаждающего воздуха н плава QJQn; в — от температуры охлаждающего воздуха <в прн drp—2 мм |
ляют из уравнения drp = 2,06do0,58. Число отверстий рассчиты вают, исходя из расхода плава через одно отверстие, считая, что скорость истечения v0 = (0,8—1,0) ф (2g#)1/2 (где ф — коэффициент скорости; Н — напор). Подробный пример расчета статического гранулятора приведен в работе [21].
Глава 6