СТВОРЕННЯ ТА ДОСЛІДЖЕННЯ. ШТУКАТУРНИХ СТАНЦІЙ І АГРЕГАТІВ. НОВОГО ПОКОЛІННЯ

Дослідження руху часток будівельного розчину при їх взаємодії’ зі стрічкою шнека та стінками бункера

Для опису роботи шнекових змішувальних пристроїв загальноприй­нято [14] розглядати рух ізольованої матеріальної точки на стрічці робочо­го органа з урахуванням впливу стінок бункера. Як зазначається у літера­турі [56, 89, 90], розчинні суміші залежно від їх стану мають одночасно властивості зв’язно-сипучих тіл і в’язких рідин. Розглянемо рух кожної елементарної частки розчинної суміші як окремого тіла за законами меха­ніки. Це дозволить нам теоретично змоделювати характер руху часток і ви­значити, які параметри головним чином впливають на нього.

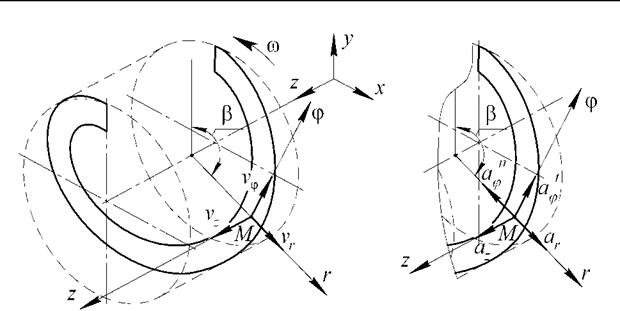
Поворотний змішувач штукатурної станції представляє собою бун­кер із розміщеним всередині нього стрічковим шнековим змішувачем (ри­сунок 3.1). Нехай крок стрічки шнека дорівнює h, внутрішній її радіус ста­новить R1, зовнішній - R2, кут, на якому внутрішня циліндрична поверхня бункера щільно прилягає до стрічки шнека становить X.

Для часток розчинної суміші, які рухаються у бункері внаслідок обе­ртання шнекової стрічки, можливі два випадки:

1) частка контактує лише зі шнеком (на всій поверхні шнекової стрі­чки, що занурена у розчин);

2) 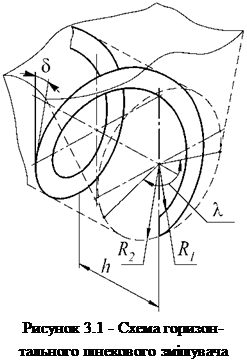частка контактує зі шнеком і внутрішньою циліндричною поверх­нею бункера (на ділянці дна бу­нкера, обмеженій кутом X).

Розглянемо спочатку перший ви­падок. Нехай дискретна частка розчину М (рисунок 3.2) рухається по внутрішній поверхні стрічки шнека. За абсолютну приймемо систему відліку xyz, жорстко зв’язану з бункером. У точці М зв’яжемо зі шнеком полярну систему координат гф z, яка обертається разом із стрічкою шнека навколо вісі z відносно бункера із постійною кутовою швидкістю ю. Слід зазначити, що радіальна координата час­тки М лежить в межах R < r < R.

Абсолютна швидкість v точки М дорівнює геометричній сумі перено­сної швидкості vnEP = ю •r точки стрічки, яка співпадає у даний момент часу з часткою М, та відносної швидкості vBI^ при рухові частки М відносно стрі­чки шнека. Проекції відносної швидкості л>Відц на осі г, ер, та z можна виразити як vr= ї, v(p = /тр, vz = z (рисунок 3.2, а). Тоді модуль відносної швидкості

Абсолютне прискорення частки Му нашому випадку буде складатися із переносного прискорення обертання стрічки шнека а ПЕР, відносного при­скорення частки при рухові відносно стрічки а Вщн та коріолісового приско­рення акор.

Переносне прискорення - це доцентрове прискорення точки шнека, котра в даний момент часу співпадає з часткою М, величина його визнача­ється як

л

аПЕР = ю ^r, (3-3)

де ю - кутова швидкість обертання шнека; r - радіус-вектор положення то­чки М.

Відносне прискорення точки М складається із наступних складових (рисунок 3.2, б):

Ъщщ=аг + а^+аг, (3.4)

де аг - радіальне прискорення, аг = г; а - прискорення частки М по ко­ординаті ер, розкладемо його на нормальну й тангенціальну складові:

и*2/ • • —► • ••

<2ф = гер ; <2ф = гв = rep; az - прискорення вздовж осі z, az = z.

Коріолісове прискорення точки у складному русі дорівнює:

де vBiffH - відносна швидкість точки М.

Спроектуємо складові абсолютного прискорення а на осі полярних координат (таблиця 3.1).

Основне рівняння динаміки для абсолютного руху частки М має вигляд:

та = У ^, (3.6)

дq т — маса частки розчину М; а — абсолютне прискорення частки М; — векторна сума прикладених до частки М сил.

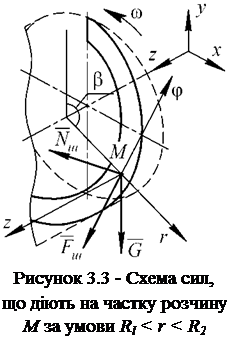
На частку М діють наступні сили (рисунок 3.3): G — сила тяжіння; Йш - нормальна реакція стрічки шнека; Рш - сила тертя по стрічці. Спрое­ктуємо ці сили на полярні осі r, ф, z.

Сила тяжіння G:

Gr = mg cos ф;

Gф = - mg sin ф;

G = 0.

Нормальна реакція стрічки шнека Йш перпендикулярна до шнекової стріч­ки (остання нахилена під кутом 5 до площини обертання) і перпендикулярна до вісі r. Причому, кут 5 визначається із співвідношення tg 5 = h2nr.

Тобто маємо:

К, = 0; К = NUI sin б; = Кш cos6. (3.7)

Напрям дії сили тертя частки М по стрічці шнека Рш визначається на­прямом дотичної до лінії перетину стрічки з уявною циліндричною поверх­нею, яка проходить через точку М, та вісь якої співпадає з віссю шнека:

F = 0; FJ = - kf Nm cos 5; FШ = kf Nm sin 5, де kf - коефіцієнт тертя1 частки розчину по стрічці шнека.

З урахуванням вищевикладеного запишемо загальні диференціальні рівняння руху дискретної частки М:

w|-co2r + г - г(ф)2 + 2со rcpj = wgcoscp; m(rg> - 2со г) = - mg sincp + Мш (sin 5 - kf cos5); mz = Nw (cos5 + kf sin5).

Тут слід відзначити, що у якості kf мається на увазі коефіцієнт тертя із урахуванням адгезії розчинної суміші із стрічкою та стінками бункера. Тобто не чисте тертя ковзан­ня розчину по сталі, а тертя ковзання основної маси суміші по тонкому шару розчину, що рухається разом із стрічкою, та по тонкому шару розчину на стінках бункера. Таким чином зазначений коефіцієнт ураховує як зовнішнє тертя суміші, так і внутрішнє.

Причому кут нахилу шнекової стрічки до площини обертання пов’язаний із радіусом r та кроком h наступним співвідношенням:

S = arctg (h/ 2 nr). (3.10)

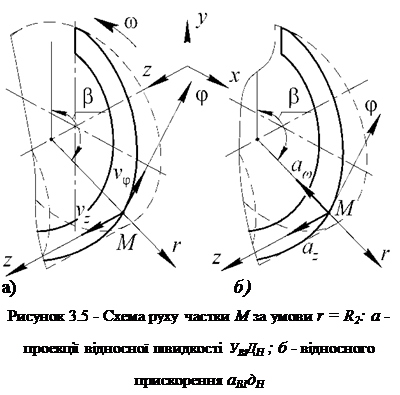
Так як форму поверхні стрічки шнека ми приймаємо гвинтовою, з твірною в будь-якій точці перпендикулярною до осі обертання шнека (пра­вильний прямий гелікоїд), то маємо:

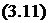h п

z = —Р.
2 n

де Р - полярний кут, що визначає положення частки М відносно шнека.

Ураховуючи (3.11), рівняння переміщення частки М по координаті ф:

• о 2п ■

ф = со —Р = со - z;

h

.. 2 71 ..

ф =--------- Z.

h

Аналізуючи систему (3.9) диференціальних рівнянь другого порядку ми бачимо, що невідомими будуть функції руху частки М: r = r (t),

ф = ф( t), z = z (t) та реакція шнека (t), котра теж буде змінювати­

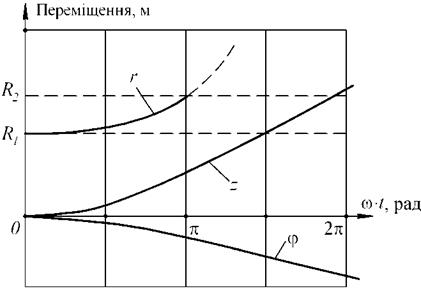
ся з часом внаслідок руху частки по стрічці. Також ми бачимо, що кінема­тичні характеристики руху часток розчину залежать як від геометричних параметрів змішувача (мінімальний та максимальний радіуси шнекової стрічки, її крок) та кінематичних характеристик руху робочого органа (ку­това швидкість шнекової стрічки), так і від властивостей самого розчину, а саме - коефіцієнта тертя розчину по стрічці та бункеру. Представлення розв’язку системи (3.9) у вигляді математичного виразу пов’язане із знач­ними складностями, але з урахуванням залежностей (3.10) та (3.12) цей розв’язок може бути знайдений чисельним методом за допомогою ПЕОМ, наприклад, з використанням математичного пакету Maple. При цьому розв’язок системи диференціальних рівнянь (3.9) представлений у вигляді графіків функцій r, ф та z залежно від кута повороту шнека для одного оберту (циклу роботи) останнього (рисунок 3.4).

Як ми бачимо, за проміжок часу, що відповідає повороту стрічки шнека на кут ~ п радіан, частка розчину проходить за координатою r відс­тань від R1 до R2 і залишає поверхню стрічки шнека (графік функції r далі показаний штриховою лінією). При цьому переміщення вздовж осі шнеко­вої стрічки (вісь z) становить величину порядку 1,1R2. Від’ємні значення функції ф свідчать про те, що в обертальному русі частка М рухається по­вільніше, ніж стрічка шнека.

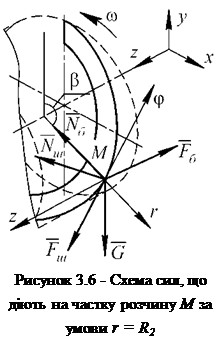
Розглянемо другий випадок. Нехай частка розчинної суміші М (ри­сунок 3.5) рухається по дну бункера на ділянці, обмеженій кутом X (див. рисунок 3.1), і контактує зі шнеком. Радіальна координата частки М у цьо­му випадку залишається сталою й дорівнює R2.

Проекції відносної швидкості Увідн на осі г, ф, та z можна виразити як vr= 0, v = г ф, vz = z (рисунок 3.5, а). Тоді модуль відносної швидкості час­тки М:

vBWH = Jvl+vl = RM+id2 ■ (з. із)

Коріолісове прискорення частки у зв’язку з тим, що r = R2= const,

а кор = 0. Відносне прискорення точки Му даному випадку буде складати­ся з наступних складових (рисунок 3.5, б):
(3.14)

де аю - доцентрове прискорення, аю=г (ф)2; а2 - прискорення вздовж осі z, a=z.

Спроектуємо складові абсолютного прискорення а на осі полярних координат (таблиця 3.2). [1]

FM, F6 - відповідно сили тертя по шнеку та бункеру. Спроектуємо ці сили на полярні осі r, cp, z.

Сила тяжіння G, як і в попередньому випадку:

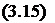
Gr = mg cos ф; Gф = - mg sin ф; Gz = 0.

Нормальна реакція бункера:

N6=-Г; Г = 0; N6 = 0.

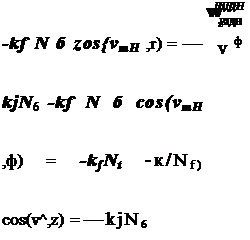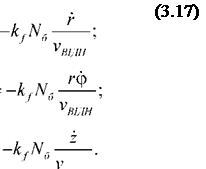Сила тертя частки М по бункеру:

де kf - коефіцієнт тертя частки розчину по бункеру та стрічці (див. зноску на стор. 58).

Так як стрічка шнека й бункер роз­чинозмішувача виготовляються з одного матеріалу - листової сталі, то коефіцієнт тертя частки розчину М по бункеру приймемо рівним коефіцієнту тертя по стрічці шнека.

Нормальна реакція шнека NM пер­пендикулярна до шнекової стрічки (остання нахилена під кутом 5 до площи­ни обертання) і перпендикулярна до вісі r. Причому, кут 5 визначається із співвід­ношення tg 5 = h/2nr = const.

Тобто маємо

К,=0-, Nl = N^sinS - К, = МШcosS. (3.18)

Напрям дії сили тертя частки М по шнековій стрічці Рш визначається напрямом дотичної до лінії перетину шнекової стрічки з внутрішньою повер­хнею бункера:

F = 0; Н, ф = - kfN,„ cos5; F = kfN„ sin5

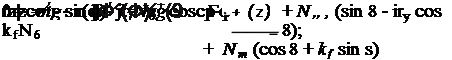Загальні диференціальні рівняння руху дискретної частки М за умови

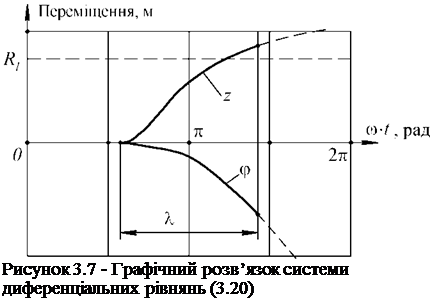в обертальному русі відбувається протилежне: до точки перегину воно зменшується повільно, а після - досить швидко.

Такий характер графіків можна пояснити наступним чином: спочатку (на першій половині ділянки X) відбувається інтенсивне переміщення час­ток суміші в осьовому напрямі вздовж осі z; потім же, внаслідок дії сил ва­ги розчину, відбувається активне проковзування часток по стрічці шнека - величина переміщення по осі z зменшується, а від’ємні значення перемі­щення ф по модулю зростають.

Виходячи із поставленого вище завдання по забезпеченню необхід­ної величини переміщення суміші у змішувачі штукатурної станції до приймальної камери розчинонасоса виникає необхідність визначення сере­дньої ШВИДКОСТІ Vz сер = z, м/с, переміщення суміші вздовж осі шнека вна­слідок обертання стрічки змішувача. Сумісний розгляд систем (3.9), (3.20) з урахуванням (3.10) - (3.12) із використанням математичного пакету Maple дозволяє одержати наближений вираз для середньої швидкості час­ток вздовж осі z:

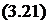vzceP= і = ^ ю2 + R2) sin 8 (cos 8-kf sin б)

Якщо останній вираз представити у вигляді графіка (рисунок 3.8), бачимо, що значною мірою на величину vZ сер впливає кутова швидкість

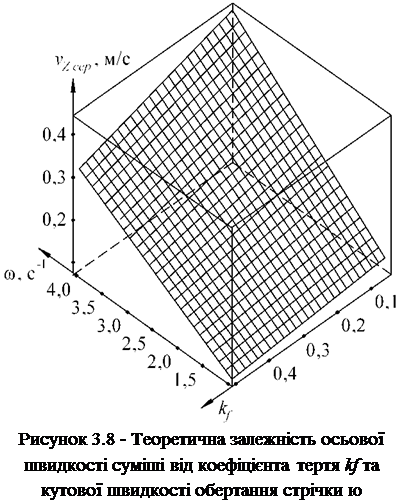стрічки. Її зростання від 1,0 до 4,0 рад/с збільшує середню швидкість осьо­вого переміщення від 0,106 до 0,424 м/с.

Тут слід зауважити, що дане значення швидкості відноситься до того об’єму суміші, що активно переміщується стрічкою шнека (тобто знахо­диться в межах радіальної координати від R1 до R2). Але ураховуючи, що питання забезпечення необхідної величини переміщення суміші до розчи­нонасоса постає, коли розчин майже весь використаним, площа S перерізу маси розчину в площині, перпендикулярній до осі z, може бути представ­лена у вигляді сегменту круга радіусом R2. Нехай Н - висота цього сегмен­ту (тобто глибина розчину, що залишився у бункері). Тоді

о

а середня величина переміщення розчину (м /год) уздовж осі z становитиме

Qz = 3600 vzсер-S. (3.23)

Слід зазначити, що останнє рівняння справедливе для рівня розчин­ної суміші Н < (R2 - R1). В інших випадках величина об’ємного перемі­щення буде меншою, адже швидкість осьового переміщення розчину, який не контактує із стрічкою шнека дещо менша [87, 94, 107].

Але, як уже зазначалося вище, величина Qz повинна бути більшою за подачу розчинонасоса протягом усього циклу роботи змішувача штукатур­ної станції чи агрегату, причому контролювати зазначену величину подачі необхідно саме наприкінці циклу роботи розчинонасоса.