Асинхронные электроприводы с векторным управлением

Система управления по вектору потокосцепления ротора приводом с синхронным двигателем

Известны многие схемы так называемых вентильных двигате­лей и бесколлекторных машин постоянного тока. Обзор подоб­ных систем с использованием регулирования модулей потоко­сцепления статора |Ws | и главного потокосцепления j^Fo) при­
веден в работе [15]. Применение принципов векторного управле­ния позволяет подойти к синтезу системы управления синхрон­ной машины с единых позиций, как это делалось для асинхрон­ных машин и машин двойного питания, поэтому будем следовать изложению, принятому в работе [7].

Наиболее просто идентифицируемой системой координат син­хронной машины является система координат (d, q), в которой ось d совпадает с магнитной осью обмотки возбуждения ротора. Опорным электромагнитным вектором в этом случае можно взять вектор потокосцепления обмотки ротора, при этом этот вектор (Фг) всегда направлен по магнитной оси обмотки ротора, так как обмотка ротора однофазная.

Система дифференциальных уравнений, описывающих дина­мику электромагнитных переменных в системе координат (d, q), имеет вид:

dl~d R9 + KRr krRr. 1 1

—-------------------------------------- Jsd - _j_ - I ^ I -)------ P®ISq + ~p (Usd + krUrd);

dt

(3.68)

dig/j R$ kg • 1

— - p - Isc - - p - p®| 4'r I - P*hd + prUaq.

dt L 0 L/r ь„

Для составляющей Isa перекрестная связь является суще­ственной, так как э. д. с. от нее определяется полной индуктив­ностью статора — pa>Lshq, поэтому в контуре необходимо при­менять прямую компенсацию этой э. д. с. с возможным использо­ванием контура с эталонной моделью. При использовании этих средств можно считать, что динамика переменных |ЧГ,.| и ha описывается линейными уравнениями с постоянными коэффи­циентами:

_ _ Rj. і ^ і + KRflsd + Ur. dlRs - f - k^.Rr Rr. 1

-~ = - - ■ :> ■ ■ I* + kr-pp-l 1 + 7T Usu

dt Ls LrLs Ls

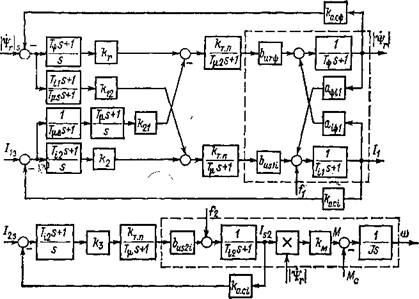
где Usi = UsdK - krUr UsdK — составляющая напряжения ста­тора по оси d с учетом компенсации э. д. с. Структурная схема привода с синхронным двигателем приведена на рис. 3.17, на ней:

Г* = Lr! Rr Tid = Ls/(Rs + klRr);

°M* = Lm’ %id *= [ WLr(Rs + W]: bur$ = Lr/Rn Krdi = — krKRs + k%); kK = (3pkr)/2; busdt - VR+W> Tiq = L'sjR - busi — /Rs.

Синтез регулятора проведем методом, близким к использо­ванному нами для привода с машиной двойного питания. Для

этого используем векторное представление системы в виде dX

*= АХ + BU* + F,

где XT = |||tr|, Isd, /„II; t/*T == II Ur, Uau U,

sq I

— T>ф CL і dtyjT

a^id/T id — T id 0 0 1 0

bur id/T id bus di/т id

о 0

Вектор напряжения U* определим как вектор напряжений на выходе преобразователей частоты в цепи статора и управляе­мого выпрямителя в цепи возбуждения ротора синхронной ма­шины, тогда

U'~*PUy, (3.71)

где

Матрицы В и Р неособенные, поэтому матрица регуляторов Z(s) может быть определена из уравнения для наперед задан­ной матрицы желаемых передаточных функций системы. Так как система является управляемой, потребуем независимости управ­ления каждой из переменных и настройки на технический опти­мум. Модельная матрица системы в этом случае будет

kZlci(2Tlss~ + + 27> +1)"1

Матрица регуляторов Z(s) получается из матричного равен­ства

Z (S) = Р-1 (s) В-1 (s) [sE - A (s)] М (s) (Е - k0. eM)~l (3.72)

и в явном виде

Z(s) =

(T^s + 1) (27V*0. сф X - at (V + 1) X о

X ky, Bbur^s) X [2TyjTфй0. с і X

Xfex. n^S+Ds]'1

- bardi (7> + 1) x Tid (Tids + 1) x o

X t(27V*0. Сф X X {2T^sTlqbas di X Xky. вbusdi) (?>+1)]-1 X К п&о, с (s)~l

0 0 (Ttqs-fl)(2riiSX

Перекрестные регуляторы, в отличие от структуры регулято­ров машины двойного питания, не используют промежуточного управляющего сигнала Us 1 = Usdx— krUr.

Канал управления модулем потокосцепления ротора 1^1 обычно используют в режиме стабилизации ІЧ^І = const. Если канал управления lSd обеспечивает стабилизацию ha = 0, то это позволяет исключить размагничивание по продольной оси маши­ны и тем самым обеспечить соотношение I'PVl = L, lr. При пра­вильной работе этих контуров параметры установившихся

UT Rrlr, Usd — Lspalsq

Usq = RsIsq + p®kr |¥r|;

Pi = UJsd + UsqIsq = RJ% + p<*kr I ¥r I /„; PQ = - UsgIs4 = LsPanq>

Р^ = рКЧгЬь

I I = LJ, v>+ /',//; - К ] T, I л/l + Lr (/;,/! Tr |!).

Анализ установившихся режимов показывает, что привод при (Vr | = const обладает значительной перегрузочной способно­стью. Она ограничивается тем, что с ростом нагрузки магнитное поле в зазоре также растет, что недопустимо в реальной ма­шине.