СОВРЕМЕННЫЕ СИСТЕМЫ УПРАВЛЕНИЯ
Чувствительность системы и корневой годограф
Одной из основных причин использования отрицательной обратной связи в системах управления является её свойство уменьшать влияние изменения параметров системы. Как мы установили в разделе 4.2, это влияние можно оценить с помощью чувствительности характеристик системы к изменению её параметров. Мы также ввели понятие логарифмической чувствительности в виде
„ т dlnT дТ/Т
S%=---------- =---------- , (7.85)
din К дК/К
где 7s) — передаточная функция системы, а К — параметр, подверженный изменению.
В последнее время, в связи с возросшим интересом к использованию плоскости для анализа свойств системы, возникла необходимость оценивать чувствительность системы по расположению корней её характеристического уравнения. Это связано с тем, что изменение параметров системы приводит к изменению положения корней характеристического уравнения, а последние, в свою очередь, определяют вид переходной характеристики системы. Поэтому мы можем ввести понятие чувствительности корней характеристического уравнения системы с передаточной функцией T(s) как
|
(7.86) |
Sr' =д '' =8- К
к din К дК/К
где гг есть i-й корень характеристического уравнения, и
m
m-о
/=і
а К — параметр системы. Эта чувствительность связывает изменение положения корня на s-плоскости с изменением параметра системы. Чувствительность корней связана с логарифмической чувствительностью соотношением
Sl L_, (7.88)
dlntf ІП'ЗІпЛ: (s+r,)
при условии, что нули Ts) не зависят от параметра К, т. е.
01п К
Логарифмическую чувствительность легко определить, взяв производную T{s) [выражение (7.87)] по параметру К. В частном случае, когда коэффициент усиления системы не зависит от параметра К, мы получим:
Sl =-Ysr' — , (7.89)
* tr А (s+n)
что даёт непосредственную связь между двумя чувствительностями.
Чувствительность корня характеристического уравнения системы довольно просто можно оценить, воспользовавшись методом корневого годографа. Для этого нам потребуются уже известные линии корней, соответствующие изменению параметра К. Мы можем придать параметру К малое конечное приращение АК и оценить новое положение корня г, + А г,. Затем, в соответствии с (7.86), мы получим
Sr‘ . (7.90)
к АК/К
Это выражение является аппроксимацией действительного значения чувствительности, которое может быть получено при АК —> 0. Оценку чувствительности корня мы проиллюстрируем следующим примером.
Пример 7.6. Чувствительность корня системы управления
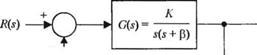
Характеристическое уравнение для системы с обратной связью, изображенной на рис. 7.23, имеет вид:
К
|
1+- |
= 0,
Ф + Р)
или
г + Рї + К = 0 . (7.91)
В качестве параметра а мы будем рассматривать коэффициент К. Тогда влияние изменения каждого параметра можно будет определить, если задать
а = а0 + Да. р = ро + др,
|
|
|
► т |
|
Рис. 7.24 Корневой годограф в зависимости от К |
|
Л |
|
і |
і |
||||||||||||
|
- Л-U. D |
|||||||||||||
|
Г /С-0 4 |
|||||||||||||
|
і |
L |
||||||||||||
|
N |
/ , |
N |
|||||||||||
|
] |
|||||||||||||
|
і |
Г |
||||||||||||
|
J |
ъ |
—0 |
|||||||||||
|
5 |
|||||||||||||
|
ч |
Г |
||||||||||||
|
J0-5 |
|
-J0 5 |
|
Л |
|
где а0 и р0— номинальные (желаемые) значения соответствующих параметров. Мы рассмотрим случай, когда ро = 1 и а0 = К = 0.5. На рис. 7.24 изображен корневой годограф в зависимости от параметра а = К, который построен по уравнению К, К |
|
1 + |
|
= 1+ |
|
= 0. |
|
(7 92) |
|
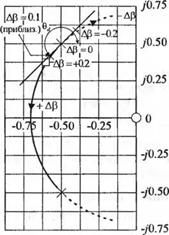
Ф + Ро) s(s+l) При номинальном значении К = а = 0,5 мы имеем два комплексных корня, г( = — 0.5 + /0,5 и г2 = ц, как показано на рис. 7.24. Чтобы исследовать влияние неизбежных вариаций параметра К, произведём замену а = а0 + Да и приведем характеристическое уравнение к виду: s2 + s + а0 + Да = s2 + s + 0.5 ± Да = 0. или ±Да, ±Да |
|
— = 0. |
|
(7.93) |
|
1 + |
|
= 1 + - |
|
s + s + 0.5 (s + fj)(s + f|) Таким образом, изменение коэффициента усиления К можно оценить по корневому годографу на рис. 7.24. При изменении а на 20% мы имеем ±Да = ± 0,1. С помощью корневого годографа легко установить новое положение корней при а = 0,4 и а = 0,6, как это показано на рис. 7.24. При а = К = 0,6 корень во 2-м квадранте s-плоскости занимает положение + Д г, = - 0,5 + у'0,59, что соответствует изменению корня Д гх = + У0.09. Если же а = К = 0.4 . то корень во втором квадранте равен г, + Д г, = - 0,5 + 70.387. что соответствует изменению корня Дг, = - j'0,11. Таким образом, чувствительность корня г, равна S? AK = = -^L = + 70,09 = >0,45 = 0,45е'90° (7.94) +АА Ki АК/К +0,2 при положительном приращении К. Для отрицательных изменений К чувствительность равна |
|
>0.11 |
|
Д'і |
|
,-/90" |
|
C'l — С'| — Л~ДК ~ лК - - |
|
= - j0,55 = 0.55е |
|
AK/K +0,2 |
При бесконечно малых изменениях параметра дК чувствительность будет равна отрицательным или положительным приращениям К. Аргумент чувствительности корня указывает на направление его смещения при изменении параметра. В точке а = а0 направление смещения корня при + Да всегда равно 180° минус направление смещения при - Да.
|
= 0. |
|
1+- |
|
|
|
Рис. 7.25. Корневой годограф в зависимости от параметра р |
|
1+ |
|
■ = 0. |
|
= 0,80е-/|3|°. |
|
(7.98) |
|
0,20 |
|
s' + s+K Знаменатель во втором слагаемом есть характеристический полином системы при Д р = 0. Для этого случая корневой годограф в зависимости от К изоб- ражен на рис. 7.24. Если по условиям синтеза требуется Поскольку корни являются комплексно-сопряженными, то -<др> |
|
форме 1 - ДР P(s) = 0. Сравнивая последнее уравнение с (7.23) (см. раздел 7.3), мы видим, что оно отличается лишь знаком второго слагаемого. Поэтому в соответствии с правилами, изложенными в разд. 7.3, мы приходим к выводу, что корневой годограф должен удовлетворять условиям | Др P(s) |=1, arg P(s) = 0° ± <5>360°, (7.97) где q = 0, 1, 2,.... Заметим, что в угловом критерии фигурирует угол 0°, в отличие от 180°, как это было в рассмотренном ранее методе. Однако правила построения корневого годографа, сформулированные в разд. 7.3, легко можно модифицировать применительно к данному случаю. На рис. 7.25 эффект уменьшения параметра р отмечен пунктирной траекторией. На том же рисунке показано положение корня при изменении р на + Д р = ± 0,20. Чувствительность корня можно оценить графически, и для положительного изменения Р она равна 0,16ej/l3l° |
|
Полюс Р может претерпевать изменения из-за влияния окружающей среды, и мы можем представить его как Р = р0 + др, где Р0 =1. Тогда характеристическое уравнение примет вид s2 + s + Др s + К = 0. или, в форме, удобной для построения корневого годографа: др. у |
|
Sr' - Ar' ■ р* (ДР/Р) |
|
S+S+ К |
|
(7.95) |
|
(7.96) |
|
При отрицательном изменении р чувствительность корня будет равна |
|
(7.99) |
|
Sn~ = р (др/р) |
Д^=0Д25^ = аб25е, з8
0,20
При уменьшении относительного изменения др/р чувствительности Л'^ и 5'1 будут стремиться
к одинаковым значениям по модулю и к разности аргументов в 180°. Так, если Др/р < 0.10, то
|5'Ч = |5'Ч (7.100)
argS^ =180°+argSpL. (7.101)
Обычно чувствительность корня определяется при малых изменениях параметра. При относительном изменении параметра Др/р = 0,10 можно воспользоваться аппроксимацией корневого годографа. На рис. 7.25 корневой годограф при ДР = 0 выходит из полюса под углом в(1. Значение этого угла легко вычислить, и тогда изменение корня можно установить, аппроксимировав корневой годограф прямой линией с наклоном вф как показано на рис. 7.25. Но подобная аппроксимация является точной только при малых приращениях Др. Однако она позволяет исследователю не прибегать к построению полного корневого годографа. Так, на рис. 7.25 чувствительность корня при Др/р = 0,10, вычисленная с помощью прямой, проведённой под углом выхода, даёт значение
S'' = 9?9?4е.'.' = 0.74е-;|35' . (7.102)
Р 0,10
Оценка чувствительности корней к изменению параметров очень полезна тогда, когда надо сравнивать влияние различных параметров при различном положении корней. Сравнение выражений (7.102) и (7.94) показывает, что модуль чувствительности к изменению Р приблизительно на 50% больше показателя для параметра а, а аргумент 5^. говорит о том, что смещение корня в
сторону мнимой оси более чувствительно к изменению параметра р. Следовательно, на изменения р должны быть наложены более строгие ограничения, чем на изменения а. Эта информация даёт возможность установить требуемые допуски на изменение каждого параметра.
Пример 7.7. Чувствительность корня к изменению параметра
Система с единичной обратной связью содержит в прямой цепи передаточную функцию
С(,) = _ВД±3) (7. ЮЗ)
s(s + 2)(s + р)
где р = р0 + Др и р0 = 8. Характеристическое уравнение системы имеет вид:
,y(.v + 2)(.v + 8 + ДР) + 20.7(.v + 3) — 0 ,
или
ф + 2)0? + 8) + ДРф + 2) + 20,7(s + 3) = 0. (7.104)
Если Др = 0, то корни уравнения равны
) = -2.36+ >2,48: г2 = г3 = - 5.27.
Корневой годограф в зависимости от ДР определяется уравнением
!+------ «4^------------- = 0. (7.105)
(s+fj)(s+/j)(s+7-3)
Полюсы и нули уравнения (7.105) показаны на рис. 7.26. Угол выхода корневого годографа из полюса /'! вычисляется следующим образом:
180° = -(Gj + 90° +0^) + (0. + 0^) = -(0j + 90° + 40°) + (133 ° + 98°) . (7.106)
Следовательно, 0(/ = - 80°, и в окрестности корня годограф аппроксимируется прямой ли
нией с углом наклона 0,;. Изменению корня Art = 0,2е~780 вдоль прямой линии соответствует приращение + Др. которое оценивается с помощью длины векторов, проведенных в точку г, из остальных полюсов и нулей. Таким образом, мы имеем:
+др = МЗ!7т2) = 0,48. (7.107)
(3,25)(2,3)
В результате чувствительность корня г, равна
Д/j 0,2е_/8О° „ _ _,80-
|
ft ft ft о -ft -ft -ft |
|
* |
|
ж -5 |
|
-3 |
|
-4 |
|
-2 |
|
-1 |
|
р |
|||||||||||
|
= ( |
|||||||||||
|
др |
А |
||||||||||
|
Ч |
др |
||||||||||
|
А |
У |
||||||||||
|
5 |
4 |
3 |
- |
1 |
к. |
||||||
|
ft ft yi >о -J1 -ft -ft |
Рис. 7.26. Положение полюсов и нулей, соответствующее параметру р
Рис. 7.27. Положение полюсов, соответствующее параметру у
а это значит, что корень очень чувствителен к изменению параметра р на 6%. Для сравнения полезно определить чувствительность /-j к изменению нуля s = — 3. В этом случае характеристическое уравнение принимает вид:
ф + 2)(s + 8) + 20,1 (s + 3 + Ду) = 0,
или
20,7Ду
|
: 0. |
|
1 + - |
(7.109)
(s+/j)(s+fj)(s+r3)
На рис. 7.27 показано положение полюсов уравнения (7.109). Угол выхода корневого годографа из полюса г, определяется из соотношения 180° = - (0(/ + 90° + 40°), или
Qii = + 50°. (7.110)
Изменению корня AT, = 0,2е,'5о° соответствует положительное приращение Ду, которое рассчитывается с помощью длины векторов как
|
(7.111) |
5,22(4.18)(0,2)
|
|Ду|= |
■ = 0,21.
20,7
Следовательно, чувствительность корня гj при + Ду равна
|
(7.112) |
S'j = = 0-2е/5° = 2.84е/50°
у Ду/у 0,21/3
Отсюда видно, что модули чувствительностей корня гх к изменению полюса Р и нуля у приблизительно равны. Однако можно считать, что чувствительность системы к изменению полюса меньше, чем её чувствительность к изменению нуля, потому что аргумент S'j равен + 50°, а это соответствует смещению корня ближе к мнимой оси.
Аналогичным образом можно показать, что чувствительность корня гх к изменению полюса s = — 80 = - 2 равна
= 2,1е/27 (7.113)
Таким образом, модуль чувствительности корня по отношению к параметру 5 меньше, чем по отношению к другим параметрам, но направление его смещения является более критическим, чем при изменениях Р и у.
Применение метода оценки чувствительности корней при анализе и синтезе систем управления требует большого количества вычислений для различного расположения полюсов и нулей передаточной функции разомкнутой системы. Этот факт, а также то, что далеко не всегда очевидно, в каком направлении должны быть изменены параметры с целью снижения чувствительности, несколько ограничивает применение данного метода при синтезе систем управления. Что же касается задач анализа, то этот метод является довольно хорошим инструментом, позволяющим оценить и сравнить чувствительность систем различной конфигурации. Недостаток метода заключается в том, что он основан на связи между положением корней на s-плоскости и качеством системы. Но как мы выяснили в предыдущих главах, во многих системах положение корней адекватно определяет показатели качества, однако в ряде случаев надо учитывать и положение нулей передаточной функции замкнутой системы. В целом же метод оценки чувствительности корней является вполне приемлемым при анализе и синтезе систем управления.