СОВРЕМЕННЫЕ СИСТЕМЫ УПРАВЛЕНИЯ

Пример синтеза с продолжением: система чтения информации с диска

В разделе 5.13 в задаче синтеза системы управления положением считывающей го­ловки мы занимались подбором коэффициента Ка. Теперь мы займемся анализом устойчивости этой системы в зависимости от параметра Ки и изменим конфигура­цию системы, как это предусмотрено шагом 4 процедуры синтеза (см. рис. 5 42).

Рассмотрим систему, изображенную на рис. 6.22. Это та же самая система с моделью двигателя и нагрузки, с которой мы имели дело в главе 5, за исключением того, что теперь в нее добавлен датчик обратной связи по скорости. Сначала рассмотрим случай, когда ключ разомкнут. Тогда передаточная функция замкнутой системы будет иметь вид:

Y(s)_ KaG,(syJ2(s)

Рис. 6.22. Замкнутая система управления положением считывающей головки с возможностью реализации обратной связи по скорости

Характеристическое уравнение системы:

s(s + 20)(s + 1000) + 5000Яа = 0 ,

или

s3 + 1020s2 + 20000s + 5000/с, = 0 .

Составим таблицу Рауса:

1 20000 1020 5000Яа ь 5000ЯИ, 20000-1020- 5000Х6 1020

Случай Ьх = 0 соответствует нахождению системы на границе устойчивости, при этом Ка = 4080. Вспомогательное уравнение имеет вид:

1020s2 + 5000 • 4080 = 0 ,

откуда следует, что на мнимой оси находятся корни s = ±у'141,4.

Чтобы система была устойчива, должно выполняться условие Ка < 4080.

Теперь введем обратную связь по скорости, замкнув ключ на рис. 6.22. Передаточная функция замкнутой системы примет вид:

Г(*)_ KaGx (s)G2(s)

Z?(s) l+[KaGx(sy32(s)](l+Kxs)'

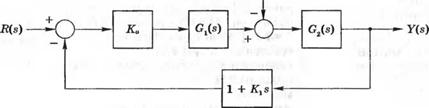
поскольку обратная связь теперь представлена фактором (1 + Kxs), как изображено на рис. 6.23.

Запишем характеристическое уравнение:

1 + [A^G1(s)G2(s)](1 + Kxs) = 0 ,

s(s + 20)(s + 1000) + 5000Л:И(1 + Kxs) = 0 .

D(s)

Отсюда имеем:

s3 + 1020Г + (20000 + 5000А„/ч)і + 5000А,, = 0 . Составим таблицу Рауса:

1 (20000+ 5000КаКх)

1020 5000/С 0

Ъх

5000Ка,

где

(20000+ 5000А:аКх )-1020- 5000АИ 1020

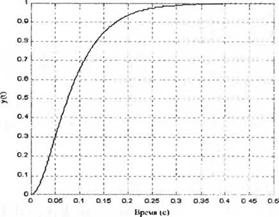
Чтобы обеспечить устойчивость системы, параметры Ки и Кх надо выбрать так, что­бы было Ьх > 0, где Ка > 0. На рис. 6.24 приведена реакция системы, рассчитанная с помо­щью MATLAB при /С, =0,05 и Яа= 100. Время установления (по критерию 2%) приблизи­тельно равно 260 мс, а перерегулирование отсутствует. Показатели качества системы приведены в табл. 6.2. Требования, предъявляемые к качеству системы, практически удовлетворены, однако требуется некоторая подгонка коэффициента Кх, чтобы добиться желаемого времени установления 250 мс.

Рис. 6.24 а)

Переходная характеристика системы с обратной связью по скорости.

(а) Скрипт MATLAB.

(б) Реакция системы при Кд= 100

и Кл = 0,05

sys=feedback(sysO, sysc); sys=minreal(sys);

t=[0:0.001:0.5];

step(sys. t);

ylabel(‘y(t)'),xlabel(‘BpeMfi (c)‘),grid

Резюме

В этой главе мы познакомились с понятием устойчивости систем управления с обратной связью. Устойчивая система была определена как система, обладающая ограниченной ре­акцией на входной сигнал. Также было показано, что устойчивость системы непосредст­венно связана с расположением полюсов ее передаточной функции на s-плоскости.

Был рассмотрен и проиллюстрирован примерами критерий устойчивости Рауса—Гур - вица. Было введено понятие относительной устойчивости, также связанное с расположе­нием на s-плоскости полюсов передаточной функции системы. Рассматривался метод анализа устойчивости систем, представленных моделью в переменных состояния.

Упражнения

У-6.1. Система имеет характеристическое уравнение s3 + 3Ks 2 + (2 + K)s + 5 = 0. Определите диапа­зон значений К, при которых система является устойчивой.

Ответ: К > 0,63.

У-6.2. Система имеет характеристическое уравнение s3 + 9s2 + 26s + 24 = 0. С помощью критерия Ра­уса-Гурвица покажите, что система устойчива.

У-6.3. Найдите корни характеристического уравнения s4 + 9,5s3 + 30.5s2 + 37s +12 = 0,

У-6.4. На рис. 6.4(У) изображена структурная схема системы управления. Определите значения ко­эффициента К, при которых система будет устойчива.

Ответ: 0 < К < 1,5 .

У-6.5. Разомкнутый контур системы с обратной связью имеет передаточную функцию

GH(s) = ,

(s + l)(s + 3)(5' + 6)

где К = 20. Вычислите корни характеристического уравнения замкнутой системы.

У-6.6. Для упражнения У-6.5 определите значение К, при котором два корня будут находиться на мнимой оси. Вычислите значения всех трех корней.

Опгеет s = —10, + j5,2.

У-6.7. Разомкнутый контур системы с отрицательной обратной связью имеет передаточную функ­цию

GH(s)=K^S+2) . ф-1)

(а) Определите значение коэффициента К, при котором коэффициент С, в замкнутой системе будет равен 0,707.

(б) Определите значение К, при котором два полюса замкнутой системы будут находиться на мнимой оси.

У-6.8. Конструкторами создан небольшой скоростной истребитель с вертикальным взлетом, неви­димый для радаров (известный как Стеле). Управление таким самолетом осуществляется с по­мощью реактивных двигателей с поворачивающимися соплами. На рис. 6.8(У) изображена си­стема управления направлением полета самолета. Определите максимально допустимое зна­чение коэффициента К, исходя из условия устойчивости замкнутой системы.

У-6.9. Дано характеристическое уравнение системы:

s3 + 3s2 + (К + l)s + 4 = 0 .

Определите диапазон значений К. при которых система устойчива.

Ответ'. К < 1/3.

У-6.І0. Для сохранения равновесия каждый человек использует органы зрения и слуха. Наша систе­ма ориентации позволяет нам сидеть или поддерживать вертикальное положение даже во вре­мя движения. Эта система действует главным образом на основе информации, принимаемой внутренним ухом, где полукружные каналы реагируют на угловое ускорение, а отолиты — на линейное ускорение. Однако измерение этих ускорений обязательно должно быть поддержано визуальной информацией. Попытайтесь проделать следующий эксперимент: (а) Поставьте одну ногу впереди другой в одну линию, а согнутые в локтях руки поставьте на бедра, (б) За­кройте глаза. Не ощущаете ли вы, что начинаете медленно раскачиваться со все увеличиваю­щейся амплитудой, пока, наконец, совсем не потеряете равновесие? Является ли ваше исход­ное положение устойчивым, если вы используете зрительный аппарат или, наоборот, выклю­чаете его из действия?

У-6.11. Система имеет передаточную функцию

Y(s) 24 (s + 1)

R(s)

s4 + 6s3 + 2s2 + s + 3

Определите установившуюся ошибку при единичном ступенчатом входном сигнале. Является ли система устойчивой?

У-6.12. В тяжелой и легкой промышленности все более широкое применение находит магнитная (бесконтактная) подвеска роторов электрических машин. Матричное дифференциальное урав­нение системы магнитной подвески имеет вид:

где х7 = [у, dy/dt. і], у—величина зазора, і—ток электромагнита. Определите, является ли сис­тема устойчивой.

Ответ-, система устойчива.

У-6.13. Система имеет характеристическое уравнение

q(s) = s6 + 9ss + 31,25s4 + 61,25s3 + 67,75s2 + 14.75s + 15 = 0 .

(а) Определите, устойчива ли система, воспользовавшись критерием Рауса-Гурвица. (б) Най­дите корни характеристического уравнения.

Ответ: (а) система находится на границе устойчивости;

(б) s = -3; -4; -1 ± 2 j: ± 0,5 j.

У-6.14. Система имеет характеристическое уравнение

q(s) = s4 + 9s3 + 45s2 + 87s + 50 = 0 .

(а) Определите, устойчива ли система, воспользовавшись критерием Рауса-Гурвица. (б) Най­дите корни характеристического уравнения.

У-6.15. Модель системы в переменных состояния задана матрицей

(а) Получите характеристическое уравнение системы, (б) Определите, является ли система устойчивой, (в) Найдите корни характеристического уравнения.

Ответ: (a) q(s) = s3 + 6s2 + 1 Is + 6 = 0.

У-6.16. Система имеет характеристическое уравнение

q{s) = s3 + 20s2 + 5s + 100 = 0.

(а) Определите, устойчива ли система, воспользовавшись критерием Рауса-Гурвица. (б) Най­дите корни характеристического уравнения.

У-6.17. Определите, устойчива или неустойчива каждая из систем, заданных своим характеристиче­ским уравнением:

(а) s3 - 4s2 + 6s + 100 = 0;

(б) s4 - 6s3 - s2 - 17s - 6 = 0;

(в) s2 + 6s + 3 = 0.

У-6.18. Найдите корни следующих уравнений:

(а) s3 + 10,4s2 + 36,2s + 40,8 = 0;

(б) s3 + 9s2 + 27s + 27 = 0 .

У-6.19. Система имеет характеристическое уравнение

q(s) = s3 + 10s2 + 29s + К = 0 .

Сдвиньте ось ординат вправо на 2 путем замены s = s„ - 2 и определите значение К, при кото­ром комплексные корни будут равны s = -2 + j.

У-6.20. Система имеет передаточную функцию T(s) = Y(s)/R(s) = І/s. (а) Является ли система устой­чивой? (б) Определите реакцию системы y(t), если r(t) — единичная ступенчатая функция.

У-6.21. Система описывается уравнением (6.22), где

О 1 О'

А= О О 1 -1 - К -2

Определите диапазон значений К, при которых система устойчива.

Задачи

3-6.1. С помощью критерия Рауса-Гурвица исследуйте устойчивость систем со следующими харак­теристическими полиномами:

(а) s2 + 5s + 2;

(б) s3 + 4s2 + 6s + 6;

(в) j3 + 2s2 - 4s + 20;

(г) s4 + s3 + 2s2 + 10s + 8;

(д) s4 + s3 + 3s2 + 2s + K:

(е) s^ + s4 + 2j3 + s + 5;

(ж) ,v5 l л-4 l 2.V3 I s~ * s і K.

Определите число корней (если таковые имеются), расположенных в правой полуплоскости. При наличии в полиноме параметра К определите диапазон значений К, при которых система устойчива.

3-6.2. В задаче 4.5 анализировалась система управления антенной и было установлено, что для уме­ньшения влияния возмущений (порывов ветра) коэффициент усиления магнитного усилителя Ка должен быть как можно больше, (а) Определите предельно допустимое значение этого ко­эффициента, исходя из соображений устойчивости системы, (б) Система должна обладать вре­менем установления, равным 1,5 с. Используя сдвиг оси ординат и критерий Рауса-Гурвица, определите значение Ка, удовлетворяющее этому условию. Предположите, что переходная ха­рактеристика в основном определяется комплексными полюсами замкнутой системы. (Спра­ведливо ли в данном случае подобное допущение?)

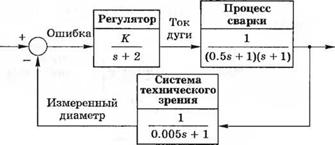
3-6.3. Одним из наиболее важных применений промышленных роботов является дуговая сварка. В большинстве ситуаций неопределенность размеров деталей, геометрии стыка и самого свароч­ного процесса требует применения специальных датчиков для обеспечения качества сварки. Некоторые роботы оснащены системой технического зрения, с помощью которой измеряется геометрия пудлинга расплавляемого металла. Подобная система изображена на рис. 6.3(3). Эта система обеспечивает постоянную скорость движения сварочного стержня вдоль шва. (а) Определите максимально допустимое значение коэффициента К, исходя из соображений устойчивости системы, (б) Выбрав значение К. ъ2 раза меньшее найденного в п. (а), определи­те корни характеристического уравнения, (в) При значении К из п. (б) определите величину перерегулирования в случае ступенчатого входного сигнала.

3-6.4. На рис.6.4(3) изображена система с об­ратной связью, в которой передаточные функции соответственно имеют вид: K(s+ 40) 1

G(s) = -

s(s + 10)

(а) Определите предельно допустимое значение коэффициента К. исходя из со­ображений устойчивости системы.

s + 20

(б) При коэффициенте К, найденном в п. (а), при котором система находится на границе устой­чивости, определите значения мнимых корней, (в) Уменьшите коэффициент К, найденный в п. (а), в 2 раза и определите относительную устойчивость системы (1) путем сдвига оси орди­нат и применением критерия Рауса-Гурвица и (2) путем определения положения полюсов. По­кажите. что полюсы расположены между —1 и -2.

3-6.5. Определите относительную устойчивость систем, заданных своими характеристическими уравнениями, путем (1) сдвига оси ординат и применения критерия Рауса-Гурвица и (2) путем определения положения комплексных корней на s-плоскости:

(a) s3 + 3s2 + 4s + 2 = 0;

(б) s4 + 9s3 + 30s2 + 42s + 20 = 0;

(b) s3+ 19s2 + 110s+ 200 = 0.

3-6.6. На рис. 6.6(3) изображена система с единичной обратной связью. Опреде­лите относительную устойчивость сис­темы по положению комплексных по­люсов на s-плоскости для следующих случаев:

65+33s

(a) G(s) = -

s (s + 9)

24

(б) G(s) =

s(s3 + 10s2 + 35s + 50)

3(s+4)(s+8)

(в) G(s) =

s(s + 5)

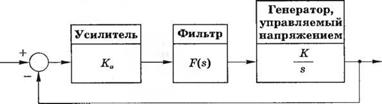
3-6.7. Линейная модель фазового детектора (контура синхронизации фазы) может быть представле­на в виде рис. 6.7(3). Устройства синхронизации фазы проектируются с целью поддержания нулевой разности фаз между входным несущим сигналом и сигналом местного генератора, управляемого напряжением. Подобные устройства применяются в цветном телевидении, в си­стемах слежения за ракетами и в космической телеметрии. В частном случае фильтр имеет пе­редаточную функцию

/■(S)-

(s+ l)(s+ 100)

(а) Определите предельно допустимое значение коэффициента Kv = КаК, исходя из условия устойчивости системы, (б) Считается приемлемым, если установившаяся ошибка будет равна 1° при скорости изменения входного сигнала 100 рад/с. Определите положение полюсов сис­темы при соответствующем значении коэффициента Kv.

3-6.8. Весьма оригинальная система была спроектирована для управления скоростью движения ин­валидного кресла на колесах. Такая система дает возможность людям, парализованным ниже шеи, передвигаться, находясь в моторизованном кресле. Структурная схема подобной систе­мы изображена на рис. 6.8(3). Датчики скорости, закрепленные на головном уборе, формиру­ют выходные сигналы, пропорциональные амплитуде движения головы. Датчики установлены под углами 90°, так что человек может отдать команду на движение вперед, назад, влево или вправо. Постоянные времени имеют типичные значения т, = 0,5 с, т3 = 1 с и т4 = 0,25 с.

(а) Определите предельно допустимое значение К = KtK2K3, исходя из условия устойчивости системы, (б) Если коэффициент К выбрать равным 1/3 от предельного значения, проверьте, возможно ли в этом случае обеспечить в системе время установления (по критерию 2%) мень­ше 4 с. (в) Найдите значение К, при котором время установления будет равно 4 с. Вычислите соответствующие этому коэффициенту корни характеристического уравнения.

3-6.9. На рис. 6.9(3) изображена система управления скоростью ленты кассетного накопителя ин­формации. (а) Определите предельно допустимое значение коэффициента К, исходя из сооб­ражений устойчивости системы, (б) Определите значение К, при котором в случае ступенчато­го входного сигнала перерегулирование составит примерно 5%.

3-6.10. В производственных операциях, требующих точности, быстроты и разнообразия действий, могут быть использованы роботы. Система управления движением руки такого робота в разо­мкнутом состоянии имеет передаточную функцию

K(s +10)

C(s)H(s) =---------- 5-----------

s(s+3)(s + 4s+8)

(а) Определите значение К, при котором в замкнутой системе возникнут незатухающие коле­бания. (б) Вычислите корни характеристического уравнения замкнутой системы при значении К, найденном в п. (а).

3-6.11. Система управления с обратной связью имеет характеристическое уравнение

s3 + (1 + K)s2 + 10s + (5 + 15/Q = 0 , причем параметр К положителен. До какого значения можно увеличивать К, прежде чем сис­тема станет неустойчивой? Если коэффициент К будет равен этому значению, в системе воз­никнут незатухающие колебания. Определите частоту этих колебаний.

3-6.12. Система имеет характеристическое уравнение

/ + 2s5 + 9s4 + 16s3 + 24s2 + 32s + 16 = 0 .

Определите, является ли система устойчивой, и вычислите корни характеристического урав­нения.

3-6.13. Проблема устойчивости системы мотоцикл-водитель является весьма актуальной, т. к. мно­гие гоночные машины трудно поддаются управлению. При построении модели такой системы надо учитывать характеристики как самой машины, так и ее водителя. В разомкнутом состоя­нии эту систему можно представить передаточной функцией [см. рис. 6.4(3)]

K(s2+ 30s +1125)

GH (s) =

s(s + 20)(s2 + 10s+ 125)(s2+ 60s+ 3400)'

(а) Аппроксимируйте систему более простой моделью, пренебрегая полиномом в числителе (нулями) и сомножителем (s2 + 60s + 3400) в знаменателе, и определите диапазон значений К. при которых замкнутая система будет устойчива.

(б) Определите действительный диапазон значений К. при которых система будет устойчива, учитывая все нули и полюсы передаточной функции.

3-6.14. Система имеет передаточную функцию

7» = - y------------------- .

s + 5s + 2s + 6

(а) Определите, устойчива ли система, (б) Вычислите корни характеристического уравнения.

(в) Постройте график реакции системы на единичный ступенчатый входной сигнал.

3-6.15. 16 июля 1993 г. в 70-этажном здании Ландмарк Тауэр в Иокогаме был введен в эксплуата­цию лифт, развивающий максимальную скорость 45 км/ч. Он был признан самым быстрым из всех существующих в мире лифтов. Чтобы достичь такой скорости, не вызывая у пассажиров неприятных ощущений, лифт ускоряется в течение несколько большего времени, чем это тех­нически возможно. Двигаясь вверх, он достигает полной скорости только к 27-му этажу; спус­тя еще 15 этажей, он начинает тормозиться. В результате его ускорение почти равно ускоре­нию, развиваемому лифтами других небоскребов — чуть менее одной десятой ускорения силы тяжести.

Чтобы сделать лифт безопасным и комфортабельным, были проявлены чудеса изобретатель­ности. Были разработаны специальные керамические тормоза, т. к. стальные просто расплави­лись бы. Управляемые с помощью компьютера системы обеспечивали гашение вибраций. Конструкция лифта имела обтекаемую форму, чтобы уменьшить сопротивление воздуха во время движения. На рис. 6.15(3) приведена система управления вертикальным положением лифта. Определите диапазон значений К, при которых сисгема устойчива.

3-6.16. Рассмотрите ситуацию с кроликами и лисами в Австралии. Число кроликов равно л,, и если бы не было хищников, то увеличивалось бы до бесконечности (если, конечно, не исчезнут ис­точники пищи), так что = kxv Однако на континенте существуют и лисы, поэтому можно считать, что і, = foe, - ах2, где х2 — число лис. Далее, лисам, чтобы существовать, необходимо наличие кроликов, поэтому х2 = - hx2 + Ъху Определите, является ли система устойчивой, и, следовательно, при t —» то придет к состоянию *,(/) = x2(t) = 0. Каким должно быть соотноше­ние между a, b, h и к, чтобы система была устойчивой? Что будет, если к больше, чем hi

Рис. 6.17 (3)

Система

управления

вертикальным

взлетом

самолета

R(s) — Желаемая траектория

Y(s)

Действительная

траектория

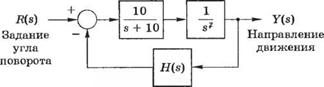
3-6.17. Самолеты с вертикальным взлетом и посадкой конструируются специально для того, чтобы они могли использовать небольшие аэропорты, а в воздухе летать как обычно. Вертикальный взлет самолета напоминает старт ракеты, поэтому объект управления объективно является не­устойчивым (см. пример 3.3, где рассматривалось поведение перевернутого маятника). В сис­теме управления самолетом, изображенной на рис. 6.17(3), используются реактивные двигате­ли с регулируемым вектором тяги, (а) Определите диапазон значений К, при которых система устойчива, (б) Определите значение К. при котором система находится на границе устойчиво­сти, и вычислите корни характеристического уравнения, соответствующие этому коэффици­енту.

3-6.18. На рис. 6.18(3), (а) изображен самолет с вертикальным взлетом, который обеспечивается че­тырьмя двигателями, вращающимися вокруг горизонтальной оси. Система управления высо­той подъема самолета приведена на рис. 6.18(3), (б).

(а) Определите, является ли система устойчивой при К = 1 .

(б) Считая К > 0, определите диапазон значений К, при которых система устойчива.

Рис. 6.18 (3)

(а) Самолет

с вертикальным взлетом.

(б) Система управления

том управления, за счет чего улучша­ется качество функционирования сис­темы. Например, при дистанционном управлении роботом бывает полезно обратную связь по положению допол­нить каналом обратной связи по уси­лию. Характеристическое уравнение системы телеуправления, изображен­ной на рис. 6.1(П), имеет вид: s4 + 20 ї3 + K, s2 + 4s + К2 = (), где К, и К2 — коэффициенты соответствующих обратных связей. Определите и представьте графически область устойчивости этой системы в плоскости параметров А', и К2.

Рис. 6.2 (П). Система управления горизонтальным положением самолета при посадке на палубу авианосца

П-6.2. Рассмотрим ситуацию с посадкой самолета на палубу авианосца. Пилот имеет три основные задачи. Во-первых, он должен обеспечить заход на посадку точно по центру посадочной поло­сы. Во-вторых, он должен выдерживать правильную глиссаду и, в-третьих, поддерживать пра­вильную скорость. На рис. 6.2(П) приведена модель системы управления горизонтальным по­ложением самолета. Определите диапазон устойчивости системы по параметру К > 0.

П-6.3. На рис. 6.3(П) изображена система управления. Требуется, чтобы система была устойчива и установившаяся ошибка при единичном ступенчатом входном сигнале не превышала 0,05 (5%). (а) Определите диапазон значений параметра а, удовлетворяющий ограничению на ве­личину ошибки, (б) Определите диапазон значений а, удовлетворяющий условию устойчиво­сти. (в) Выберите значение а, удовлетворяющее обоим требованиям.

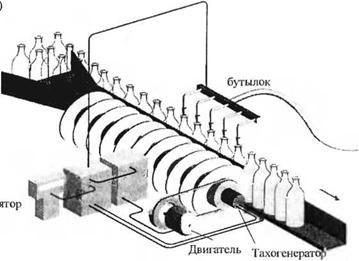
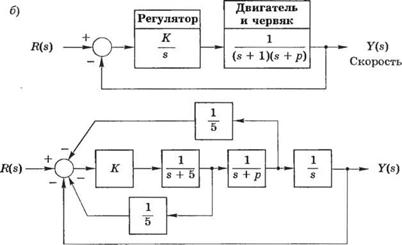
П-6.4. На рис. 6.4(П) изображена линия разлива жидкости в бутылки, в которой используется чер­вячный подающий механизм. Точное значение скорости ленты поддерживается за счет тахо­метрической обратной связи. Определите и представьте графически область устойчивости си­стемы в плоскости параметров Кир.

Задачи на синтез систем

СС-6.1. В системе управления приводом скользящей части стола металлообрабатывающего станка (см. задачу СС-5.1) регулятор был представлен обычным усилителем. Определите, до каких пор можно увеличивать коэффициент Ка, прежде чем система станет неустойчивой.

С-6.1. Система управления зажиганием автомобильного двигателя должна нормально работать в широком диапазоне изменения параметров. Структурная схема такой системы изображена на рис. 6.1 (С), где выбору подлежит коэффициент усиления регулятора К. Параметрр для многих автомобилей равен 2, но для машин высокого класса он может равняться нулю. Выберите та­кой коэффициент К, при котором система будет устойчива в любом из указанных случаев.

С-6.2. Автоматический самоходный аппарат для исследования поверхности Марса можно предста­вить структурной схемой на рис. 6.2(C). Аппарат имеет два рулевых колеса, расположенных спереди и сзади, а по условиям синтеза H(s) = Ks + 1. Определите (а) диапазон значений К. при которых система устойчива, (б) значение К, при котором один корень характеристического уравнения будет равен s = -5, и (в) значения двух остальных корней при коэффициенте К. най­денном в п. (б), (г) Определите реакцию системы на ступенчатый входной сигнал при коэффи­циенте К, найденном в п. (б).

Рис. 6.5 (С). Система управления дорожным движением

С-6.5. Система управления дорожным движением, изображенная на рис. 6.5(C), предназначена для обеспечения определенной дистанции между движущимися транспортными средствами, (а) Определите диапазон значений К, при которых система устойчива, (б) Если Кт есть максима­льное значение К, при котором корни характеристического уравнения оказываются на мнимой оси, то примите К = KJN, где 6 < N < 7. Требуется, чтобы время максимума переходной харак­теристики было менее 2 с, а перерегулирование не превышало 18%. Выберите соответствую­щее значение N.

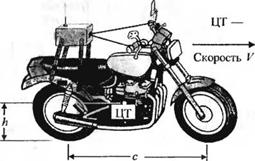
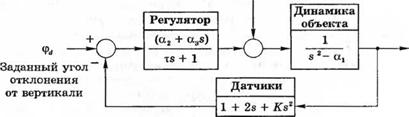
С-6.6. На рис. 6.6(C). (а) показано, как с помощью робота можно управлять мотоциклом. Соответст­вующая структурная схема приведена на рис. 6.6(C), (б). Определите диапазон значений К, при которых система устойчива, если а | =g/h = 9, а2 = V~/hc= 2,7 иа3 = V/hc = 1,35. Предпола­гается, что мотоцикл движется с постоянной скоростью V =2 м/с. Постоянная времени регуля­тора т = 0,2 с, а К > 0.

Рис. 6.6 (С)

(а) Мотоцикл, управляемый роботом.

(б) Структурная схема системы

Задачи, решаемые с помощью MATLAB

М-6.1. Найдите корни характеристических уравнений:

(а) q(s) = s3 + 3s2 + 5s + 7 = 0;

(б) ф) = і-4 + 3s3 + 4s2 + 4s + 10 = 0;

(в) g(s) = s4 + 2s2 + 1 = 0.

M-6.2. Рассмотрите систему с единично» отрицательной обратной связью, которая в разомкнутом состоянии имеет передаточную функцию

j + 2s + 1

С помощью MATLAB найдите корни характеристического уравнения замкнутой системы при К = 1. 2 и 5. При каких значениях К замкнутая система устойчива?

М-6.3. Система с единичной отрицательной обратной связью в разомкнутом состоянии имеет пере­даточную функцию

G(s) = -^------- ^

s + 4 s + 6s+ 10

С помощью MATLAB получите передаточную функцию замкнутой системы и покажите, что ее характеристическое уравнение имеет корни її = -2,89 и s23 = -0,55 ± >1,87.

М-6.4. Дана передаточная функция

T(s) =-------------------------------- .

ї5 + 2 s4 + 2 s3 + 4s2+ ї+ 2

(а) С помощью критерия Рауса-Гурвица определите, является ли система устойчивой. Если она неустойчива, то сколько полюсов находится в правой полуплоскости? (б) С помощью MATLAB вычислите полюсы T(s) и проверьте результат, полученный в п. (а), (в) Постройте график реакции системы на ступенчатый входной сигнал и обсудите результат.

Рис. 6.5 (М). Самолет с пилотом в контуре управления

+ .

s + 5s + (К - 3)s + К

М-6.5. При синтезе и анализе систем управления самолетами часто используется модель «бумажно­го пилота», которая включается в замкнутый контур. Структурная схема самолета с пилотом «в контуре» изображена на рис. 6.5(М). Вносимое пилотом запаздывание представлено пара­метром т. Для пилота с замедленной реакцией можно принять т = 0,5 с, а для пилота с более быстрой реакцией т = 0,25 с. Остальные параметры модели пилота имеют следующие значе­ния: К= 1. т, = 2 с. т, = 0.5 с. С помошью MATLAB вычислите полюсы замкнутой системы, со­ответствующие разным пилотам, и прокомментируйте результаты. Чему равно максимально допустимое время запаздывания пилота, при котором система еще остается устойчивой?

М-6.6. Рассмотрите систему с обратной связью, изображенную на рис. 6.6(М). Используя функцию for, составьте программу MATLAB, которая вычисляла бы полюсы замкнутой системы для 0 < К < 5 и строила диаграмму их расположения, помечая символом «х». С помощью критерия Рауса-Гурвица определите диапазон значений К, при которых система устойчива. Вычислите корни характеристического уравнения при значении К. минимально допустимом из соображе­ний устойчивости.

М-6.7. Система представлена в переменных состояния следующими уравнениями:

у=[1 1 0]х.

(а) С помошью функции poly получите характеристическое уравнение системы, (б) Вычислите корни характеристического уравнения и определите, является ли система устойчивой

(в) Изобразите графически реакцию системы y(t), если n(t) — единичное ступенчатое воздей­ствие, а начальные условия — нулевые.

Ключевые термины и понятия

Вспомогательный полином. Выражение, образованное с помощью элементов строки, непосредст­венно предшествующей нулевой строке таблицы Рауса.

Критерий Рауса-Гурвица. Правило, позволяющее исследовать устойчивость системы путем ана­лиза ее характеристического уравнения. Критерий утверждает, что число корней характери­стического уравнения с положительной действительной частью равно числу изменений знака элементов первого столбца таблицы Рауса.

Относительная устойчивость. Свойство системы, оцениваемое величиной действительной части корней характеристического уравнения.

Устойчивая система. Динамическая система, обладающая ограниченной реакцией на ограничен­ный входной сигнал.

Устойчивость. Важнейшее свойство системы. Система является устойчивой, если все полюсы ее передаточной функции имеют отрицательные действительные части.