СОВРЕМЕННЫЕ СИСТЕМЫ УПРАВЛЕНИЯ
Анализ устойчивости с помощью MATLAB
Этот раздел мы начнем с критерия Рауса-Гурвица и покажем, какое простое и удобное средство предоставляет MATLAB для вычисления корней характеристического уравнения. Если характеристическое уравнение содержит один варьируемый параметр, то можно отразить в виде диаграммы изменение положения корней в зависимости от этого параметра.
В данном разделе будет введена функция for, с помощью которой последовательность инструкций повторяется заданное число раз.
Критерий Рауса-Гурвица. Как было отмечено выше, критерий Рауса-Гурвица определяет необходимое и достаточное условие устойчивости. Если задано характеристическое уравнение с постоянными коэффициентами, то с помощью критерия Рауса-Гурвица можно определить число корней, расположенных в правой полуплоскости. Например, рассмотрим характеристическое уравнение замкнутой системы, изображенной на рис. 6.10:
q(s) = s3 + s2 + 2s + 24 = 0 .
|
+ |
|
Д(«)—*0 |
|
Y(s) |
|
G(s) — 3 2 |
|
s + s + 2s + 23 |
|
Рис. 6.10 Замкнутая система управления с передаточной функцией As) = y[s)/ff(s) = = l/Cs3 + s2 + 2s + 24) |
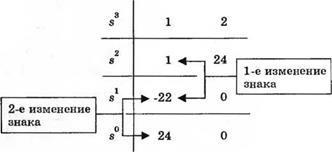
Соответствующая таблица Рауса приведена на рис. 6.11. Два изменения знака в первом столбце указывают на наличие двух корней уравнения в правой полуплоскости; следовательно, замкнутая система неустойчива. С помощью MATLAB мы можем проверить этот результат, непосредственно вычислив корни характеристического уравнения, как это показано на рис. 6.12. Для этого необходимо использовать функцию pole, которая вычисляет корни алгебраического полинома.
|
|
|
Рис. 6.11 Таблица Рауса для замкнутой системы с передаточной функцией 7s) = 1AS3 + s2 + 2s + 24) |
Рис. 6.12
Использование функции pole для вычисления полюсов замкнутой системы, изображенной на рис. 6.10
|
»numg=[1]; deng=[1 1 2 23]; sysg=tf(numg, deng); |
||
|
»sys=feedback(sysg.[1]); |
||
|
»pole(sys) |
||
|
ans = |
||
|
-3.0000 |
||
|
1 0000 + 2 < |
Корни в правой |
|
|
1.0000-2.6458І |
полуплоскости |
|
Л » |
К |
1 |
||
|
J * |
s + 2s2 + 4s |
|||
|
+ |
|
R(s)- |
|
Y(s) |
|
Если характеристическое уравнение является функцией единственного параметра, то q(s) = s3 + 2r + 4s + К = 0 . Рис. 6.13 Замкнутая система = K/(s? + 2s2 + 4s + К) |
|
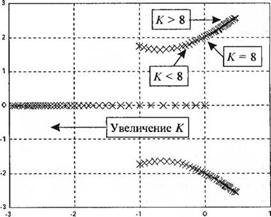
С помощью критерия Рауса-Гурвица мы нашли (см. уравнение 6.12), что система устойчива при 0 < К < 8. Этот результат можно проверить графически с помощью MATLAB. Как показано на рис. 6.14(a), мы задали диапазон значений К, при которых хотим вычислить корни характеристического уравнения. Затем с помощью функции roots вычислили и изобразили траектории корней. Как видно из графика, с увеличением К корни характеристического уравнения смещаются вправо, при К = 8 они оказываются на мнимой оси, а при К > 8 попадают в правую полуплоскость. Программа на рис. 6.14 содержит функцию for. Эта функция обеспечивает выполнение одной и той же серии инструкций заданное число раз. Она в сочетании с инструкцией end образует цикл повторяющихся вычислений. На рис. 6.15 приведен формат функции for, а также пример ее использования. В примере цикл повторяется 10 раз. На /-м шаге, где 1 < і < 10, г'-й элемент вектора а устанавливается равным 20, а скаляр Ъ пересчитывается. Критерий Рауса-Гурвица позволяет получить однозначный ответ на вопрос об абсолютной устойчивости линейной системы, В то же время он не позволяет судить об относительной устойчивости, которая непосредственно связана с положением корней характеристического уравнения. Критерий Рауса-Гурвица говорит о том, сколько корней находится в правой полуплоскости, но не указывает конкретного положения этих корней. С помощью MATLAB мы можем вычислить точные значения корней и тем самым судить об относительной устойчивости системы. Пример 6.10. Управление поворотом гусеничной машины На рис. 6.8 изображена структурная схема системы управления поворотом гусеничной машины. Цель синтеза состоит в выборе параметров К и а, при которых система будет устойчива и установившаяся ошибка при линейном входном сигнале не будет превышать 24% от величины этого сигнала. Для решения этой задачи можно воспользоваться критерием Рауса-Гурвица. Характеристическое уравнение замкнутой системы имеет вид: |
Рис. 6.14
|
Действительная ось |
|
а) |
(а) Траектории корней уравнения q (s) = s3 + 2s2 + + 4s + К = О
при О < К < 20.
(б) Скрипт MATLAB
|
б) |
% Этот скрипт вычисляет корни характеристического % уравнения q(s)=sA3+2sA2+4s+K при 0<К<20 %
К=[0:0.5:20]; for i=1 :length(K) ^
|
Цикл для вычисления корней в функции от К |
q=[1 2 4 K(i)]; U-------
p(:,i)=roots(q); J end
plot(real(p),imag(p),‘x')1grid
хІаЬеІ(‘Действительная ось'),уІаЬеІ(‘Мнимая ось')
|
Общий формат
|
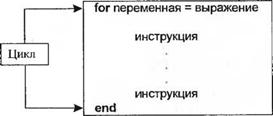
Рис. 6.15
Функция for и иллюстративный пример
Инструкция end вводится для указания окончания цикла
Пример
for і = 1:10 <~ а(і)=20; Ч - b=a(i)+2*i; end ▲
Счетчик і
а — вектор из 10 элементов
Ъ — скаляр, изменяющий значение при увеличении г
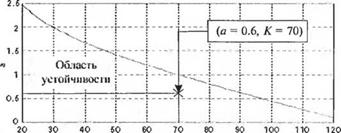
Составив таблицу Рауса, мы получим два условия устойчивости: К < 126 и Ка > 0. Это значит, что мы можем ограничить область поиска значениями 0 < К < 126 и а > 0. Сначала с помощью MATLAB мы найдем границу устойчивости в плоскости параметров К и а. Затем мы сможем найти пары значений (К, а), принадлежащих области устойчивости, таких, которые удовлетворяли бы ограничению на установившуюся ошибку. Эта процедура, показанная на рис. 6.16, включает в себя задание диапазона значений К и а и вычисление корней характеристического уравнения для конкретных значений этих параметров. Для каждого К мы найдем первое значение а, при котором по крайней мере один корень характеристического уравнения попадает в правую полуплоскость. Этот процесс повторяется до тех пор, пока не будет пройден весь диапазон значений К и а. Найденные пары чисел (К', а) определяют границу между областями устойчивости и неустойчивости.
На рис. 6.16 область слева от графика зависимости а =/(К) является областью устойчивости. Если считать, что r(t) = At, I > 0, то установившаяся ошибка
s(s + 1)(ї + 2)(і + 5) А 10 А
= І1Ш5 =------------------------------------------------------------------- .
s(s + l)(s + 2)(s + 5) + K(s + a) s
Ka
|
E(s)- |
|
■ад- |
|
При заданном ограничении ess < 0,24А мы имеем:-------------------------- < 0.24 Д или Ка Ка > 41,67. |
|
(6.31) |
|
где мы использовали тот факт, что 1 |
|
1 + GcG(s) |
|
•ад= |
|
s{s + l)(s + 2)(s + 5) s(s + l)(s + 2)(s + 5) + К (s + a) 10 A |
|
a) |
|
|
Рис. 6.16
(а) Область устойчивости в плоскости параметров (К, а) для системы управления поворотом гусеничной машины.
(б) Скрипт MATLAB
|
б) |
|
Диапазон значений А’ и а |
|
Задание начальных значений векторов диаграммы соответствующей длины |
|
Характеристический полином |
|
n=length(K); m=length(a); for i=1 :n forj=1:m q=[1,8,17,K(i)+10,K(i)*a(j)]; p=roots(q); if max(real(p))>0, x(i)=K(i);y(i)=a(j-1); break; end end i_________________________ ^___________ end |
|
% Определение области устойчивости для системы % управления поворотом гусеничной машины % а=[0.1:0.01:3.0];К=[20:1:120]; х=0*К; у=0*К; < |
|
Определение первого значения а, приводящего к неустойчивости при заданном К |
|
plot(x, y),grid, xlabel(‘K’), ylabel(‘a’) |
Любые значения К и а, лежащие в области устойчивости на рис. 6.16 и удовлетворяющие условию (6.31), будут считаться приемлемыми. Например, значения К = 70 и а = 0,6 будут удовлетворять всем выдвинутым требованиям. При этих значениях передаточная функция замкнутой системы примет вид:
70s+42
Т (S) - —І------ 5 Ч------------- •
s4 + 8s3+17r+80s+42
Полюсы замкнутой системы будут иметь значения:
s = -7,0767, і = -0,5781, 5 = -0.1726 + 3,1995/ и і = -0,1726 - 3,1995/.
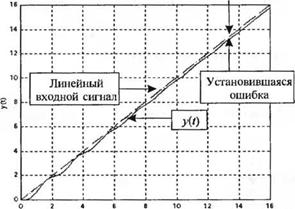
Реакция системы на линейный входной сигнал, изменяющийся с единичной скоростью, приведена на рис. 6.17. Установившаяся ошибка менее 0,24, как и требовалось.
|
В|>смя (с* |
|
о) |
Рис. 6.17
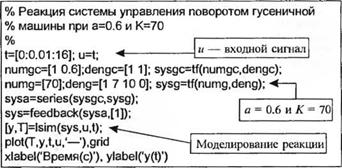
(а) Реакция системы управления поворотом гусеничной машины на линейный входной сигнал при К = 70 и a = 0,6.
(б) Скрипт MATLAB
|
|
б)
Устойчивость систем, описываемых переменными состояния. Обратимся теперь к анализу устойчивости систем, представленных моделью в переменных состояния. Предположим, что мы имеем дело с системой, описываемой уравнением (6.22). Ее устойчивость можно определить по характеристическому уравнению, которое записывается через матрицу А:
Левая часть этого уравнения является полиномом от s. Если все корни характеристического уравнения имеют отрицательные действительный части, т. е. Re s, < 0, то система устойчива.
Если модель системы представлена в переменных состояния, то прежде всего необходимо найти ее характеристический полином. Это можно сделать несколькими способами. Один из них предполагает раскрытие определителя (si - А) вручную. После этого можно либо вычислить корни характеристического уравнения с помощью функции MATLAB roots, либо использовать критерий Рауса-Гурвица, чтобы установить, имеются ли корни в правой полуплоскости. К сожалению, ручные вычисления могут вызвать затруднения, особенно при большой размерности матрицы А. Избежать подобных неприятностей можно, если прибегнуть к помощи MATLAB.
Характеристическое уравнение можно получить с помощью функции poly, рассмотренной в разделе 2.10. Напомним, что эта функция позволяет образовать полином по вектору его корней. Ее также можно использовать для вычисления характеристического уравнения матрицы А, как показано на рис. 6.18, где матрица А задана в виде
-8 -16 -6
А= 1 0 0
0 1 0
а в результате вычислений получен полином
s3 + 8s2 + 16s + 6 .
Если А — матрица размерности п х п, то функция poly(A) возвращает вектор-строку из п + 1 элементов, являющихся коэффициентами характеристического уравнения.
|
Рис. 6.18 Вычисление |
|
Коэффициенты характеристического полинома по убывающим степеням |
|
»А=[-8 -16 -6:1 0 0 ;0 1 0]; »p=poly(A) |
|
Р = |
|
1.0000 8.0000 16.0000 6.0000 |
|
»roots(p) |
|
ans = |
|
Матрица п х п |
|
характеристического полинома матрицы А с помощью функции poly |
|
p=poly(A) |
|
Характеристический полином |
|
-5.0861 -2.4280 -0.4859 |
|
Система устойчива |
Пример 6.11. Определение области устойчивости в случае неустойчивого объекта
На рис. 6.19 изображена система управления реактивным самолетом. Предположим, что z > 0 и р > 0. В разомкнутом состоянии система неустойчива, т. к. ее характеристическое уравнение имеет вид:
s(s - l)(s + р) = s[i2 + (р - l)s - р] = 0 .
|
R(s) |
|
—-У(*) Действительная ориентация |
|
Заданная ориентация |
|
Регулятор |
Самолет |
|
|
K(s + г) |
1 |
|
|
(s + р) |
s(s - 1) |
Рис. 6.19. Система управления реактивным самолетом
Заметим, что поскольку один член в квадратных скобках является отрицательным, то характеристическое уравнение имеет по крайней мере один корень в правой полуплоскости. Характеристическое уравнение замкнутой системы имеет вид:
s3 + (р -1>2 + (К-p)s + Kz = 0 .
Определим область устойчивости в пространстве параметров К, риг. Составим таблицу Рауса:
і Ск-р)
(р-1) Kz
ь2
Kz,
где
U _ (p-l)(K-p)-Kz
2 : •
р-1
Согласно критерию Рауса-Гурвица, мы должны потребовать выполнения условий Kz > 0 и р > 1. Полагая Ъ2 = 0, получим:
(р - Ш-Р) - Kz = K[(p-l)-z] - р{р - 1) = 0 .
Следовательно, должно выполняться условие:
|
К >- |
Р(Р - О
(6.33)
(p-)-z Рассмотрим три случая:
.z>(p— 1). Т. к. р> 0, то любое значение К > 0 будет удовлетворять условиям устойчивости.
2. z=(p-l). Не существует таких К,(0<К<сю), при которых система была бы устойчива.
3. z < (р — 1). При заданных риг существует значение К. (0 < К < оо), удовлетворяюшее условию устойчивости (6.33).
Условия устойчивости можно изобразить графически. На рис. 6.20 приведен скрипт MATLAB, позволяющий построить границу устойчивости в трехмерном пространстве. В скрипте использована функция mesh для построения трехмерной поверхности и функция meshgrid для вычисления массивов данных, входных для mesh.
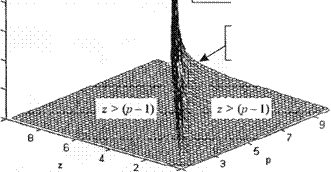
На рис. 6.21 приведена трехмерная диаграмма для определения области устойчивости в координатах К, р и z.
|
Рис. 6.20 Скрипт MATLAB для определения области устойчивости |
|
Область значений р и z для построения сетки Поверхность устойчивости |
|
% Определение области устойчивости % системы управления реактивным % самолетом в трехмерном пространстве % [p, z]=meshgrid(1.2:0.2:10.0.1:0.2:10); ч------- k=p*(p-1)./(p-1-z);4- mesh(p, z,k)-< |
|
Построение трехмерной диаграммы |
|
Рис. 6.21 Г раница устойчивости в трехмерном пространстве |
|
Область устойчивости находится над поверхностью устойчивости |
|
|
|
Поверхность устойчивости |
|
400 |