СОВРЕМЕННЫЕ СИСТЕМЫ УПРАВЛЕНИЯ
Устойчивость систем, описываемых переменными состояния
Устойчивость системы можно определить и по ее модели в переменных состояния. Если система задана своей передаточной функцией
Ф)
гдеp(s) и q(s) — полиномы от переменной s, то ее устойчивость определяется корнями характеристического уравнения q(s) = 0. Чтобы система была устойчива, все корни этого уравнения должны быть расположены в левой половине s-плоскости. Итак, для ответа на вопрос об устойчивости системы, описываемой передаточной функцией, мы используем характеристическое уравнение и применяем критерий Рауса-Гурвица. Если же система представлена в виде сигнального графа в переменных состояния, то определитель этого графа совпадает с характеристическим полиномом, к которому легко применить уже известный критерий. Проиллюстрируем это несколькими примерами.
Пример 6.7. Устойчивость системы
Рассмотрим систему из примера 3.1, которая имеет передаточную функцию
T(s)= 2д2+8д+6 , (6.20)
s + 8s + 16s + 6
Характеристический полином этой системы
g(s) = s3 + 8s2 + 16s + 6 . (6.21)
Этот характеристический полином также легко можно получить по любой из моделей системы в виде сигнального графа, представленных на рис. 3.12 и рис. 3.13. С помощью критерия Рауса-Гурвица можно убедиться, что все корни q(s) расположены в левой полуплоскости, следовательно, система устойчива.
Часто модель системы бывает задана в виде совокупности дифференциальных уравнений относительно переменных состояния. В этом случае удобно изобразить альтернативную модель в виде сигнального графа, по которому легко записать его определитель
A(s) и, следовательно, характеристическое уравнение. Освоить этот прием нам поможет
следующий пример.
Пример 6.8. Устойчивость системы второго порядка
Система второго порядка описывается двумя дифференциальными уравнениями первого порядка:
л, = -З*, + х2, х2=х2- Кх} + Kit,
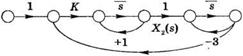
где u(t) — входной сигнал, а точки над л, символизируют производные по времени. Модель в виде сигнального графа, соответствующая этим уравнениям, изображена на рис. 6.7. Граф содержит три контура:
I, = s~ L2 = -3s-1 и L3 = -Ks~2, причем Lx и L2 не имеют общего узла. Следовательно, по правилу Мейсона, определитель графа
Д = 1 - (L, + L2 + L3) + L, L2 = 1 - (s_1 - 3s-' - Ks~2) + (-3s"2) .
Умножив А на s2, получим характеристическое уравнение
s2 + 2s + (К - 3) = 0 .
Поскольку для устойчивости все коэффициенты должны быть положительны, то мы приходим к условию К> Ъ.
|
|
Рис. 6.7
Сигнальный граф для системы из примера 6.8
Метод получения характеристического уравнения непосредственно по векторному дифференциальному уравнению основан на том, что для свободного движения системы решение имеет вид экспоненциальной функции. При отсутствии входных сигналов векторное дифференциальное уравнение имеет вид
х = Ах, (6.22)
где х — вектор состояния. Поскольку решение такого уравнения представляет собой экспоненту, то мы можем найти такие константы X, при которых решение для каждой пере
менной состояния будет иметь видх, (О = к, ех‘1. Константы X, называются характеристическими числами или собственными значениями системы, они же являются корнями характеристического уравнения. Если положить х = кеА(, то подставив это выражение в (6.22), получим:
Хкех' = Аке'1, (6.23)
или
Хх = Ах. (6.24)
Уравнение (6.24) можно переписать в виде
(XI - А)х = 0, (6.25)
где I — единичная матрица, 0 — нулевая матрица. Нетривиальное решение этой системы однородных уравнений существует тогда и только тогда, если обращается в нуль определитель матрицы (A. I — А), т. е. если
det(Xl - А) = 0. (6.26)
Раскрывая определитель, мы получим уравнение п-го порядка относительно X, которое и будет характеристическим уравнением системы. Далее не составит труда исследовать устойчивость системы. Для иллюстрации этого метода рассмотрим систему третьего порядка, с которой мы имели дело в примере 3.2.
Пример 6.9. Замкнутая система распространения эпидемии
|
-а |
-р |
0 |
1 |
0' |
Uj |
|
|
р |
-у |
0 |
х + |
0 |
1 |
|
|
а |
У |
0 |
0 |
0 |
-и2. |
В примере 3.2 была рассмотрена модель динамики эпидемического заболевания. Соответствующее векторное дифференциальное уравнение имеет вид (3.55). и мы воспроизведем его еще раз:
dx ~dt
|
Отсюда получим характеристическое уравнение:
|
= ЭД(Х.+ ы)(Х.+ у)+ Р2 ] = !{>? + (а + уЯ+ (ау + р2)]= 0.
Это уравнение очень похоже на характеристическое уравнение (3.57), полученное по сигнальному графу. Дополнительный корень X = 0 появился из-за того, что имеется переменная л3, являющаяся интегралом от (ах| + ух2), но хъ не влияет на остальные переменные состояния. Поэтому корень X = 0 указывает просто на наличие интегратора, формирующего переменную х3. Характеристическое уравнение показывает, что при (а + у) > 0 и (ау + Р") > 0 система будет находиться на границе устойчивости.
В заключение рассмотрим еще раз перевернутый маятник, модель которого была получена в примере 3.3. Система имеет матрицу
'0 1 0
|
А = |
-mg/М 0
gU
|
=х2х2 - I |
|
= Х |
|
= 0. |
|
det |
|
/ |
|
Характеристическое уравнение det(>J - А) = 0 принимает вид: ~Х -1 О О О X mg/M О 0 0 >i-l 0 0 - g/l X |
Анализ этого уравнения показывает, что имеются два корня X = 0, корень X = ^J— и g
корень X = - J^. Следовательно, система неустойчива, т. к. один из корней расположен в
правой полуплоскости. Два корня в начале координат будут приводить к возникновению неограниченно нарастающей реакции.